17.1.1. Mary and John

Here is a very simple database of facts about a problem domain.

(define the-rules
  '(((mary likes wine))
    ((mary likes cheese))
    ((john likes beer))
    ((john likes wine))
    ((john likes chips))
    ((person mary))
    ((person john))))
[download]

Our database is called the-rules and it is a list of statements of various sorts. This database lists facts about what mary and john like, and also the facts that both mary and john are people. There is nothing special about the structure of these individual facts, just as long as we remain consistent in their use, and write queries that interrogate the database appropriately. In other words it is we, the programmers, who decide the “meaning” of ((mary likes wine)): the system attaches no particular significance to that structure in itself; in particular likes is not a keyword or an operator of the logic programming system, it is just a symbol that I have chosen to use.

In our logic programming implementation, we will use symbols with initial capital letters as pattern variables which can match parts of the database. So given the database above, the system can respond to a query such as (mary likes X) with the facts (mary likes wine) and (mary likes cheese), and can respond to the question (person X) with the facts (person mary) and (person john). Of course there is nothing here that a simple SQL query could not do, so let's make things more interesting by adding a rule to the facts.

This rule states “mary likes anyone who likes chips.” This is written as:

((mary likes X) (person X) (X likes chips))
[download]

You can read this as “mary likes X if person X and X likes chips.”

Rules all have this general form. The first statement in the rule is true if all of the other statements in the rule are true or can be proved to be true. The first statement is called the head of the rule, and the remaining statements are called the body of the rule.

Looked at in this way, bare facts are just rules with no body: they are true in themselves because there is nothing left to prove. This explains the apparently redundant extra parentheses around each fact in our example database.

Given our extended database, which now looks like this:

(define the-rules
  '(((mary likes wine))
    ((mary likes cheese))
    ((john likes beer))
    ((john likes wine))
    ((john likes chips))
    ((person mary))
    ((person john))
    ((mary likes X) (person X) (X likes chips)))
[download]

the system can answer the question (mary likes john) in the affirmative, and furthermore, when prompted to list all the things that mary likes with (mary likes X), john will be among the results:

> (prove '((mary likes X)))
> ?
((mary likes wine))
> ?
((mary likes cheese))
> ?
((mary likes john))
[download]

Also note that the statement to be proved has those apparently redundant extra braces too. This is because the system can be asked to prove any number of things at once, for example:

> (prove '((mary likes X) (X likes beer)))
((mary likes john) (john likes beer))
> ?
Error: no more solutions
[download]

This can be read as “prove mary likes X and X likes beer.” The query only succeeds if all of the components succeed, so it is just like the body of a rule in this respect.

17.1.2. J. S. Bach and Family

This type of programming can also be used for recursive search. Figure 17.1 shows a small snippet of the Bach family tree, with old J. S. at the centre.

We can translate that into the following facts:

(((johann ambrosius) father-of (j s)))
(((j c friedrich) father-of (w f ernst)))
(((j s) (anna magdalena) parents-of (j c friedrich)))
(((j s) (anna magdalena) parents-of (johann christian)))
(((j s) (maria barbara) parents-of (wilhelm friedmann)))
(((j s) (maria barbara) parents-of (c p e)))
[download]

Now, we have a mixture of facts about fathers alone, and parents where the mother is known. But we can rectify that with a few extra rules as follows:

((X father-of Y) (X _ parents-of Y))
((X mother-of Y) (_ X parents-of Y))
((X parent-of Y) (X father-of Y))
((X parent-of Y) (X mother-of Y))
[download]

That underscore is a special pattern variable that always matches anything. The first rule then says “X is the father of Y if X and anybody are parents of Y” (the parents-of facts always list the father first.) Likewise the second rule says “X is the mother of Y if anybody and X are parents of Y.” The last pair of rules (actually really one rule in two parts) says that “X is a parent of Y if X is the father of Y or X is the mother of Y.”

So we have a general way of expressing both and and or in our rules: and is expressed by adjacent statements in the body of a single rule, while or is expressed as alternative versions of the same rule.

Now that we have a general parent-of relation, we can add a recursive ancestor-of relationship as follows:

((X ancestor-of Y) (X parent-of Y))
((X ancestor-of Y) (X parent-of Z) (Z ancestor-of Y))
[download]

This says “X is an ancestor of Y if X is a parent of Y or X is a parent of some Z and Z is an ancestor of Y.” Given that definition, and the rest of the facts and rules, we can start to ask interesting questions of the system:

> (prove '((X ancestor-of (w f ernst))))
(((j c friedrich) ancestor-of (w f ernst)))
> ?
(((johann ambrosius) ancestor-of (w f ernst)))
> ?
(((j s) ancestor-of (w f ernst)))
> ?
(((anna magdalena) ancestor-of (w f ernst)))
> ?
Error: no more solutions
[download]

We can add yet more rules to this database. For example X and Y are siblings if X and Y have the same parent:

((X sibling-of Y) (Z parent-of X)
                  (Z parent-of Y)
                  (require (not (eq? 'X 'Y))))
[download]

If we don't require that X and Y are not equal then this rule would think that old J. S. was his own brother. Given that, we can ask:

> (prove '(((c p e) sibling-of X)))
(((c p e) sibling-of (johann christian)))
[download]

etc.

17.1.3. Appending Lists

In case you're starting to think that logic programming is just some sort of glorified database lookup, here's a more meaty example. Consider the problem of appending two lists. You can write an append function in PScheme very easily⁵³ as:

(define append
  (lambda (a b)
    (if a
        (cons (car a)
              (append (cdr a)
                      b))
        b)))
[download]

It walks to the end of the list a, then at that point returns the list b, and as the recursion unwinds it builds a copy of a prepended to b. So for example:

> (append '(a b) '(c d))
(a b c d)
[download]

This definition is useful enough in itself, but logic programming allows a much more flexible definition of append as follows:

(define the-rules
  (list '((append () Y Y))
        '((append (A . X) Y (A . Z)) (append X Y Z))))
[download]

Note that this uses the PScheme dotted pair notation introduced in Section 8.4.1. So the expression (A . X) refers to a list who's car is A and who's cdr is X.

The first rule says that the result of appending something to the empty list is just that something. The second rule says that you can join (A . X) and Y to make (A . Z) if you can join X and Y to make Z.

Why is that more powerful than the PScheme append? Because we can ask lots of questions of it. Not only can we ask “what do we get if we append (a b) and (c d)?”:

> (prove '((append (a b) (c d) X)))
((append (a b) (c d) (a b c d)))
[download]

We can also ask “what do we need to append to (a) to get (a b c d e)?”:

> (prove '((append (a) X (a b c d e))))
((append (a) (b c d e) (a b c d e)))
[download]

And even “what can we append together to make (a b c d)?”:

> (prove '((append X Y (a b c d))))
((append () (a b c d) (a b c d)))
> ?
((append (a) (b c d) (a b c d)))
> ?
((append (a b) (c d) (a b c d)))
> ?
((append (a b c) (d) (a b c d)))
> ?
((append (a b c d) () (a b c d)))
> ?
Error: no more solutions
[download]

This idea is absolutely core to the concept of logic programming. A rule that states that “A and B make C” is equally capable of describing “what do I need to make C?” provided C has a value when the question is asked. It is as if the relationship described by the rule can be inspected from many different angles when seeking a solution to a problem.

Back to append. The rules for append can of course be made available to other rules, for example (peeking ahead a bit)

((sentence S) (append NP VP S) (noun-phrase NP) (verb-phrase VP))
[download]

Says S is a sentence if you can append NP and VP to make S, and NP is a noun phrase, and VP is a verb phrase. Rules for noun-phrase and verb-phrase would be very similar, and rules for individual words would just be of the form ((noun (garage))) etc.

17.1.4. Factorial Again

The above examples have already demonstrated that our database of rules can be recursive, so how about the king of recursive functions, our old friend the factorial function? Here it is recast into a pair of rules:

(define the-rules
  (list
     '((factorial 0 1))
     '((factorial N X) (T is (- N 1)) (factorial T U) (X is (* N U)))))
[download]

This isn't as bad as it might first look. The first rule is the bare fact that the factorial of 0 is 1. The second rule says that the factorial of N is X if T is N - 1 and the factorial of T is U and X is N * U. The special infix is operator forces arithmetic evaluation of its right hand side, then requires that its left hand side is the same as the result of that evaluation.

given the above we can calculate factorials:

> (prove '((factorial 10 X)))
((factorial 10 3628800))
[download]

However there is a limitation here. Because of the unidirectional nature of that is operator, we cannot ask “what number can we apply factorial to to get x”:

>(prove '((factorial X 3628800)))
Error: no more solutions
[download]

So it goes.

17.1.5. Symbolic Differentiation

If you're still not impressed, how about a more difficult problem? I hope you don't mind a little maths. This next example states some of the rules of symbolic differentiation then asks the system to work out the differential of an equation. The rules we'll be using are:

• The derivative of x in x is 1.
• The derivative of any constant number in x is 0.
• The derivative of xn in x is n×xn-1.
• The derivative of f+g in x is df+dg if the derivative of f in x is df and the derivative of g in x is dg.
• The derivative of f-g in x is df-dg if the derivative of f in x is df and the derivative of g in x is dg.
• The derivative of f×g in x is f×dg+g×df if the derivative of f in x is df and the derivative of g in x is dg.
• The derivative of 1/f in x is -df/f2 if the derivative of f in x is df.
• The derivative of f/g in x is (g×df - f×dg)/f2 if the derivative of f in x is df and the derivative of g in x is dg.

If you don't remember the maths from school, just sit back and enjoy the ride. These rules can translate directly into our logic system as:

(define the-rules
  (list '((derivative X X 1))
        '((derivative N X 0) (require (number? 'N)))
        '((derivative (X ^ N) X (N * (X ^ P))) (P is (- N 1)))
        '((derivative (F + G) X (DF + DG))
            (derivative F X DF)
            (derivative G X DG))
        '((derivative (F - G) X (DF - DG))
            (derivative F X DF)
            (derivative G X DG))
        '((derivative (F * G) X ((F * DG) + (G * DF)))
            (derivative F X DF)
            (derivative G X DG))
        '((derivative (1 / F) X ((- DF) / (F * F)))
            (derivative F X DF))
        '((derivative (F / G) X (((G * DF) - (F * DG)) / (G * G)))
            (derivative F X DF)
            (derivative G X DG))))
[download]

This is obviously way more complex than Mary and John, but there isn't actually much that you haven't seen before. The first and most important thing to realise is that, with one exception, the arithmetic operators “+”, “-” etc. mean nothing special to the logic program: they are just symbols in patterns to be matched. Having said that we do need ways to perform numeric tests and to do arithmetic. The body of second rule requires that N is a number, and the body of third rule evaluates (- N 1) before “assigning” it to P. Rules of the form (require ‹expr›) and (‹var› is ‹expr›) are recognized and treated specially by the system.

Anyway, having entered these rules we can ask the system:

(prove '((derivative
            (((x ^ 2) + x) + 1)
            x
            X)))
[download]

That is to say “prove the differential of x2 + x + 1 in x is X”. The system replies:

((derivative
  (((x ^ 2) + x) + 1)
  x
  (((2 * (x ^ 1)) + 1) + 0)))
[download]

The last line is the computed value for X, the pattern variable in the query. For now we will have to simplify that manually:

(((2 * (x ^ 1)) + 1) + 0)
  (2 * x      ) + 1
[download]

You can see that the result is indeed the differential of x2 + x + 1, namely 2x + 1.

---

That should be enough to whet your appetite for what the rest of this chapter has to offer. We next turn our attention to pattern matching, which is the basis of unification, which along with amb from the previous chapter is the basis of our logic programming implementation.

17.2.1. A Perl Pattern Matcher

As I've said, pattern matching is merely a precursor to unification, which is our goal. Implementing a pattern matching system in Pscheme is fairly trivial, either in the PScheme language itself or in the underlying Perl, but we're not actually going to do that, because it isn't powerful enough for our purposes. However we need to start somewhere, so this section discusses a standalone pattern-matching implementation in Perl. It's easy enough to understand, and the subsequent section builds on that to produce a standalone unification implementation. Having arrived at a standalone unification implementation, we can wire that in to our interpreter.

But first we need to look at pattern matching. This standalone Perl pattern matcher can take patterns of the form:

['a', { b => 'X'}, 'Y']
[download]

where capitalized strings represent the pattern variables. It matches them against structures such as

['a', { b => [2, 3] }, 'c']
[download]

returning a hashref that will look like

{ X => [2, 3], Y => 'c' }
[download]

Here's a birds-eye view of how our first pattern matcher will work. It walks both the pattern and the structure in parallel, also passing an additional, initially empty environment around. If it encounters a variable in the pattern then it checks to see if the variable is already set in the environment. If it is, then it checks that the current structure component is the same as the value of the variable, failing if it is not. If the variable is not set in the environment, it extends the environment, binding the variable to the current structure component, and continues. Of course matching will also fail if the pattern and the structure are not otherwise identical. On success, it returns the environment, and on failure, it dies.

Both for the fun of it, and for completeness' sake, the pattern matcher described here can handle perl hashrefs as well as listrefs. This means it will accept patterns and structures containing mixtures of both types. However only the values of a hash in a pattern will be recognised as pattern variables, the keys will not.

Here's the top-level match() routine:

sub match {
    my ($pattern, $struct, $env) = @_;
    $env ||= {};
    if (var($pattern)) {
        match_var($pattern, $struct, $env);
    } elsif (hashes($pattern, $struct)) {
        match_hashes($pattern, $struct, $env);
    } elsif (arrays($pattern, $struct)) {
        match_arrays($pattern, $struct, $env);
    } elsif (strings($pattern, $struct)) {
        match_strings($pattern, $struct, $env);
    } else {
        fail();
    }
    return $env;
}
[download]

Firstly, if $env is not passed, then match() initializes it to an empty hashref. The pattern matching algorithm is never required to undo any variable bindings that it creates, so we can just pass around a hash by reference and allow the bindings to accumulate in it. Then we see various tests for the types of $pattern and $struct. The var() check is just:

sub var {
    my ($thing) = @_;
    !ref($thing) && $thing =~ /^[A-Z]/;
}
[download]

So a var is any string that starts with a capital letter.

The hashes() check returns true if both arguments are hashrefs:

sub hashes {
    my ($a, $b) = @_;
    hash($a) && hash($b);
}
[download]

Where hash() is just:

sub hash {
    my ($thing) = @_;
    ref($thing) eq 'HASH';
}
[download]

The other two checks, arrays() and strings() are defined equivalently:

sub arrays {
    my ($a, $b) = @_;
    array($a) && array($b);
}

sub array {
    my ($thing) = @_;
    ref($thing) eq 'ARRAY';
}

sub strings {
    my ($a, $b) = @_;
    string($a) && string($b);
}

sub string {
    my ($thing) = @_;
    !var($thing) && !ref($thing);
}
[download]

Ok, that's the administrative support out of the way.

So the first thing that match() does, if its $pattern is a var(), is to call match_var() on the $pattern and the $struct, passing the current environment. Here's match_var():

sub match_var {
    my ($var, $struct, $env) = @_;
    if (exists($env->{$var})) {
        match($env->{$var}, $struct, $env);
    } else {
        $env->{$var} = $struct;
    }
}
[download]

It checks to see if the $var is in the environment. If it is then it attempts to match() the value of the variable against the $struct⁵⁵. If the $var is not already in the environment then it puts it there with a value equal to the current $struct (an unassigned variable will always match the current structure component, and will be instantiated to it.)

Returning to match(), if both the $pattern and the $struct are arrays(), match() calls match_arrays() on them.

match_arrays() walks both arrays in tandem, calling match() on each pair of elements. If the arrays are not the same length then they cannot possibly match, so this sanity check is performed first:

sub match_arrays {
    my ($pattern, $struct, $env) = @_;
    my @patterns = @$pattern;
    my @structs = @$struct;
    if (@patterns != @structs) { fail(); }
    while (@patterns) {
        match(shift @patterns, shift @structs, $env);
    }
}
[download]

The fail() sub dies with a "match failed" message:

sub fail { die "match failed\n"; }
[download]

Back to match() again. If the $pattern and the $struct are both hashes(), then match() calls match_hashes() on them:

sub match_hashes {
    my ($pattern, $struct, $env) = @_;
    check_keys_eq($pattern, $struct);
    foreach my $key (sort keys %$pattern) {
        match($pattern->{$key}, $struct->{$key}, $env);
    }
}
[download]

Much as match_arrays() checks that the two arrays are the same length, match_hashes() checks that the two hashes have the same keys using check_keys_eq():

sub check_keys_eq {
    my ($as, $bs) = @_;
    my $astr = join('.', sort keys %$as);
    my $bstr = join('.', sort keys %$bs);
    fail unless $astr eq $bstr;
}
[download]

This is a cheap trick and could easily be fooled, but it's good enough for our demonstration purposes.

Assuming that the hashes have equal keys (this pattern matcher does not allow—or at least expect—hash keys to be variables), match_hashes() walks the keys matching the individual components in much the same way as match_arrays() did. It sorts the keys before traversing them to ensure the order of any variable assignment is at least deterministic.

Back to match() yet again. If both the $pattern and the $struct are strings(), match() calls match_strings() on them. This is the most trivial of the matching subroutines: it just compares the strings and fails if they are not equal:

sub match_strings {
    my ($pattern, $struct, $env) = @_;
    fail if $pattern ne $struct;
}
[download]

This completes our prototype pattern matching implementation.

While very simple, this pattern matcher can be made to do useful work. Consider a “database” of facts in a Perl list:

my @facts = (
    {
        composer => 'beethoven',
        initials => 'lv',
        lived => [1770, 1829]
    },
    {
        composer => 'mozart',
        initials => 'wa',
        lived => [1756, 1791]
    },
    {
        composer => 'bach',
        initials => 'js',
        lived => [1685, 1750]
    }
);
[download]

We can use the matcher to extract information from this list:

foreach my $fact (@facts) {
    eval {
        my $result = match({
            composer => 'COMPOSER',
            initials => 'js',
            lived => 'LIVED'
        }, $fact);
        print "The composer with initials 'js'",
              " is $result->{COMPOSER}",
              " who lived from $result->{LIVED}[0]",
              " to $result->{LIVED}[1]\n";
    };
}
[download]

That's it for pattern matching. We next turn our attention to Unification, which as I've said is an extension to Pattern Matching and is much more interesting.

17.3.1. A Perl Unifier

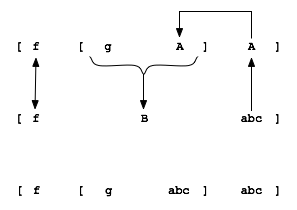
This unifier can solve a broader class of problems than a simple pattern matcher can. For example given the two patterns:

['f', ['g', 'A'], 'A']
[download]

and

['f', 'B', 'abc']
[download]

It can correctly deduce:

A => 'abc',
B => ['g', 'abc']
[download]

You can see the process graphically in Figure 17.2. The variable 'A' unifies with the term 'abc' while the variable 'B' unifies with the compound term ['g', 'A'], where 'A' is provided with a value 'abc' from the previous unification.

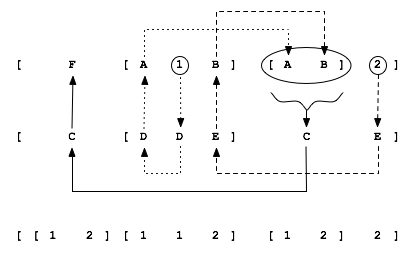
Unification is capable of even more complex resolutions, for example it can unify (ommitting quotes for brevity this time)

[F, [A, 1, B], [A, B], 2]
[download]

with

[C, [D, D, E], C, E]
[download]

To show that

• A = 1
• B = 2
• C = [1, 2]
• D = 1
• E = 2
• F = [1, 2]

You can see this in action in Figure 17.3 if you just follow the differently styled arrows starting from the three ringed nodes in the figure as they propogate information around.

---

This unifier has additional feature: the anonymous variable “_” (underscore) behaves like a normal variable but will always match anything, since it is never instantiated. This allows you to specify a “don't care” condition. For example, going back to our database of composers, the pattern:

{
    composer => 'COMPOSER',
    initials => '_',
    lived => '_'
}
[download]

will just retrieve all of the composers names from the database, without testing or instantiating any other variables. Not also that since “_” always matches, and is never instantiated, it can be reused throughout a pattern.

This unifier is a direct modification of the pattern matcher from the previous section, so let's just concentrate on the differences. Firstly match() has been renamed to unify(), and it has an extra clause, in case the old structure, which is now also a pattern, contains variables. The various match_* subs have also been renamed unify_*, and the variables $pattern and $struct, now both patterns, have been renamed to just $a and $b:

sub unify {
    my ($a, $b, $env) = @_;
    $env ||= {};
    if (var($a)) {
        unify_var($a, $b, $env);
    } elsif (var($b)) {
        unify_var($b, $a, $env);
    } elsif (hashes($a, $b)) {
        unify_hashes($a, $b, $env);
    } elsif (arrays($a, $b)) {
        unify_arrays($a, $b, $env);
    } elsif (strings($a, $b)) {
        unify_strings($a, $b, $env);
    } else {
        fail();
    }
    return $env;
}
[download]

The extra clause, if $b is a var, simply reverses the order of the arguments to unify_var(). Note that the single environment means that variables will share across the two patterns. If you don't want this, simply make sure that the two patterns don't use the same variable names.

unify_hashes(), unify_arrays() and unify_strings() are identical to their match_* equivalents, except that unify_arrays() and unify_hashes() call unify() instead of match() on their components.

The var() check is slightly different, to allow for the anonymous variable:

sub var {
    my ($thing) = @_;
    !ref($thing) && ($thing eq '_' || $thing =~ /^[A-Z]/);
}
[download]

That leaves unify_var(), where the action is. unify_var() is still quite similar to match_var(), it just has more things to watch out for:

sub unify_var {
    my ($var, $other, $env) = @_;
    if (exists($env->{$var})) {
        unify($env->{$var}, $other, $env);
    } elsif (var($other) && exists($env->{$other})) {
        unify($var, $env->{$other}, $env);
    } elsif ($var eq '_') {
        return;
    } else {
        $env->{$var} = $other;
    }
}
[download]

So $struct was renamed to $other, and unify_var() calls unify() instead of match(). If $var is not set in the environment, instead of immediately assuming it can match $other, unify_var() looks to see if $other is a var and already has a value. If so it calls unify() on $var and the value of $other. If $other is not a var, or has no binding, unify_var() next checks to see if $var is the anonymous variable. If it is, then because the anonymous variable always matches and is never instantiated, it just returns. Lastly, only when all other options have been tried, it adds a binding from the $var to $other and returns.

Let's walk through the actions of unify() as it attempts to unify the two patterns ['f', ['g', 'A'], 'A'] and ['f', 'B', 'abc'].

• unify(['f', ['g', 'A'], 'A'], ['f', 'B', 'abc'], {}) is called with the two complete patterns and an empty environment, and determines that both patterns are arrays, so calls unify_arrays().
  • unify_arrays(['f', ['g', 'A'], 'A'], ['f', 'B', 'abc'], {}) simply calls unify() on each component.
    • unify('f', 'f', ()) determines that both its arguments are strings, and calls unify_strings().
      • unify_strings('f', 'f', {}) = {} succeeds but the environment is unchanged.
    • unify(['g', 'A'], 'B', {}) determines that it's second argument is a variable and so calls unify_var() with the arguments reversed.
      • unify_var('B', ['g', 'A'], {}) = {B => ['g', 'A']} succeeds, and unify_var() extends the environment with 'B' bound to ['g', 'A'].
    • unify('A', 'abc', {B => ['g', 'A']}) determines that it's first argument is a variable and so calls unify_var() again, passing the environment that was extended by the previous call to unify_var().
      • unify_var('A', 'abc', {B => ['g', 'A']}) = {B => ['g', 'A'], A => 'abc'} also succeeds, extending the environment with a new binding of 'A' to 'abc'. This environment is the final result of the entire unification.

So the final result {B => ['g', 'A'], A => 'abc'} falls a little short of our expectations, because the value for 'B' still contains a reference to the variable 'A'⁵⁶. However this is not a problem as such. we can patch up the result with a separate routine called resolve().

sub resolve {
    my ($pattern, $env) = @_;
    while (var($pattern)) {
        if (exists $env->{$pattern}) {
            $pattern = $env->{$pattern};
        } else {
            return $pattern;
        }
    }
    if (hash($pattern)) {
        my $ret = {};
        foreach my $key (keys %$pattern) {
            $ret->{$key} = resolve($pattern->{$key}, $env);
        }
        return $ret;
    } elsif (array($pattern)) {
        my $ret = [];
        foreach my $item (@$pattern) {
            push @$ret, resolve($item, $env);
        }
        return $ret;
    } else {
        return $pattern;
    }
}
[download]

resolve() takes a pattern, and the environment that was returned by unify(). If and while the pattern is a variable, it repeatedly replaces it with its value from the environment, returning the variable if it cannot further resolve it. Then if the result is a hash or an array reference, resolve() recursively calls itself on each component of the result, also passing the environment. The final result of resolve() is a structure where any variables in the pattern that have values in the environment have been replaced by those values. Note that resolve() does not change the environment in any way.

This completes our stand-alone implementation of unify(). Hopefully seeing it out in the open like this will make the subsequent implementation within PScheme easier to digest. It is a little difficult to demonstrate the utility of unify() at this point, since it's purpose is mostly part of the requirements of logic programming, however to give you some idea, consider that the result of one unification, an environment or hash, can be passed as argument to a second unification, thus constraining the values that the pattern variables in the second unification can potentially take.

There is one extremely interesting and useful application of unification outside of logic programming which makes use of this idea. Consider that we might want to check that the types of the variables in a PScheme expression are correct before we eval the expression. Assume that we know the types of the arguments and return values from all primitives in the language. Furthermore we can also detect the types of any variables which are assigned constants directly. It is therefore possible to detect if a variable's assigned value does not match it's eventual use, even if that eventual use is remote (through layers of function calls) from the original assignment. Such a language, which does not declare types but is nonetheless capable of detecting type mismatches, is called an implicitly typed language. We can use unification to do this type checking, by treating PScheme variables as pattern variables and unifying them with their types and with each other across function calls, accumulating types of arguments and return values for lambda expressions and functions in the process.

That however, is for another chapter. Next we're going to look at the implementation of unify in PScheme.

17.3.2. Implementing unify in PScheme

To get the ball rolling with the implementation of unify, notice that the previous implementation of unify() frequently tests the types of its arguments. Obviously in an object-oriented implementation like PScheme we can distribute a Unify() method around the various data types and avoid this explicit type checking for the most part.

A second point worth noting is that where the above unify() did a die on failure, our new Unify() can quite reasonably invoke backtracking instead, to try another option, which fits in quite neatly with our existing amb implementation.

A third and final point. unify() above made use of a flat hash to keep track of variable bindings, but PScheme already has a serviceable environment implementation and we should make use of it. This will mean exposing the environment as a PScheme data type since that is what is explicitly passed to and returned by Unify(), but this is not a concern since we have done this once before in our classes and objects extension from Chapter 12.

We'd better start by looking at the unify command in action in the interpreter. The result of a call to unify is a PScm::Env which isn't much direct use. However we can add another PScheme command that will help us out there. substitute takes a form and an environment, and replaces any pattern variables in the form with their values from the argument environment. It also performs the resolve() function on each value before substitution. So for example:

> (substitute
>     '(f B A)
>     (unify '(f (g A) A)
>            '(f B abc)))
(f (g abc) abc)
[download]

The call to unify provides the second argument, an environment, to substitute, which then performs the appropriate replacements on the expression (f B A) to produce the result (f (g abc) abc). Note that in all cases we have to quote the expressions to prevent them from being evaluated. We do need the interpreter to evaluate the arguments to substitute and unify in most cases however, because the actual forms being substituted and unified may be passed in as (normal PScheme) variables or otherwise calculated.

I should probably also demonstrate that unify does proper backtracking if it fails:

> (unify '(a b c) '(a b d))
Error: no more solutions
[download]

It's still somewhat difficult to demonstrate the usefulness of unify combined with amb at this stage however. That will have to wait until the next section where we finally get to see logic programming in action.

The first thing we need to do then, is to create a new special form PScm::SpecialForm::Unify and give it an Apply() method. This special form will be bound to the symbol unify in the top-level environment. unify will take two or three arguments. The first two arguments are the patterns to be unified. The third, optional argument is an environment to extend. If unify is not passed an environment, it will create a new, empty one. We have to make unify a special form because it needs access to the failure continuation. Here's PScm::SpecialForm::Unify:

504 package PScm::SpecialForm::Unify;
505 
506 use base qw(PScm::SpecialForm);
507 
508 use PScm::Continuation;
509 
510 sub Apply {
511     my ($self, $form, $env, $cont, $fail) = @_;
512     $form->map_eval(
513         $env,
514         cont {
515             my ($evaluated_args, $fail) = @_;
516             my ($a, $b, $qenv) = $evaluated_args->value;
517             $qenv ||= new PScm::Env();
518             $a->Unify($b, $qenv, $cont, $fail);
519         },
520         $fail
521     );
522 }
523 
524 1;

You can see that it uses map_eval() from Section 13.6.5 to evaluate its argument $form, passing it a continuation that breaks out the patterns $a and $b, and the optional environment $qenv from the evaluated arguments. Then it defaults $qenv to a new, empty environment, and calls Unify() on $a passing it the other pattern, the query environment and the success and failure continuations.

Referring back to our test implementation of unify() in Section 17.3.1 we can see that the first thing that implementation does is to check if its first argument is a var, and if so call unify_var() on it. We can replace this explicit conditional with polymorphism by putting a Unify() method at an appropriate place in the PScm::Expr hierarchy. But the PScm::Expr::Symbol class is not the best place: not all symbols are pattern variables, only those starting with capital letters or underscores. So here's the trick. We create a new subclass of PScm::Expr::Symbol called PScm::Expr::Var and put the method there. Read() can detect pattern variables on input and create instances of this new class instead of PScm::Expr::Symbol. Since the new class inherits from PScm::Expr::Symbol, and we do not override any of that class's existing methods, these new PScm::Expr::Var objects behave exactly like ordinary symbols to the rest of the PScheme implementation. Here's the change to _next_token() from PScm::Read to make this happen.

 66 sub _next_token {
 67     my ($self) = @_;
 68 
 69     while (!$self->{Line}) {
 70         $self->{Line} = $self->{FileHandle}->getline();
 71         return undef unless defined $self->{Line};
 72         $self->{Line} =~ s/^\s+//s;
 73     }
 74 
 75     for ($self->{Line}) {
 76         s/^\(\s*// && return PScm::Token::Open->new();
 77         s/^\)\s*// && return PScm::Token::Close->new();
 78         s/^\'\s*// && return PScm::Token::Quote->new();
 79         s/^\,\s*// && return PScm::Token::Unquote->new();
 80         s/^\.\s*// && return PScm::Token::Dot->new();
 81         s/^([-+]?\d+)\s*//
 82           && return PScm::Expr::Number->new($1);
 83         s/^"((?:(?:\\.)|([^"]))*)"\s*// && do {
 84             my $string = $1;
 85             $string =~ s/\\//g;
 86             return PScm::Expr::String->new($string);
 87         };
 88         s/^([A-Z_][^\s\(\)]*)\s*//
 89           && return PScm::Expr::Var->new($1);
 90         s/^([^\s\(\)]+)\s*//
 91           && return PScm::Expr::Symbol->new($1);
 92     }
 93     die "can't parse: $self->{Line}";
 94 }

The only change is on Lines 88–89 where if the token matched starts with a capital letter or underscore then _next_token() returns a new PScm::Expr::Var where otherwise it would have returned a PScm::Expr::Symbol.

Now we have somewhere to hang the functionality equivalent to unify_var() from our test implementation, we can put it in a method called Unify() in PScm::Expr::Var:

378 sub Unify {
379     my ($self, $other, $qenv, $cont, $fail) = @_;
380 
381     if (defined(my $value = $qenv->LookUpNoError($self))) {
382         $value->Unify($other, $qenv, $cont, $fail);
383     } elsif ($other->is_var &&
384              defined (my $other_value = $qenv->LookUpNoError($other))) {
385         $other_value->Unify($self, $qenv, $cont, $fail);
386     } elsif ($self->is_anon) {
387         $cont->Cont($qenv, $fail);
388     } else {
389         $qenv->ExtendUnevaluated(
390             new PScm::Expr::List($self),
391             new PScm::Expr::List($other),
392             $cont,
393             $fail
394         );
395     }
396 }

It's identical to the earlier unify_var() except that it makes use of method calls and is written in CPS. The is_var() method is defined to be false at the root of the expression hierarchy in PScm::Expr, but is overridden to be true in PScm::Expr::Var alone. Equivalently is_anon() is defined false in PScm::Expr but defined to be true if the value of the var is “_” in PScm::Expr::Var⁵⁷:

400 sub is_anon {
401     my ($self) = @_;
402     $self->value eq '_';
403 }

The only other occurrence of Unify() is at the root of the hierarchy in PScm::Expr:

 49 sub Unify {
 50     my ($self, $other, $qenv, $cont, $fail) = @_;
 51     if ($other->is_var) {
 52         $other->Unify($self, $qenv, $cont, $fail);
 53     } else {
 54         $self->UnifyType($other, $qenv, $cont, $fail);
 55     }
 56 }

This really just takes care of the case where the first pattern is not a var but the second pattern is. If the second pattern is a var it calls Unify() on it, passing $self as the argument, reversing the order in the same way as our prototype unify() did. If the second pattern is not a var, then it calls a new method UnifyType() on $self. UnifyType() is just another name for Unify() and allows a second crack at polymorphism since it is implemented separately in a couple of places in the PScm::Expr hierarchy.

The first such place is in PScm::Expr itself.

 58 sub UnifyType {
 59     my ($self, $other, $qenv, $cont, $fail) = @_;
 60     if ($self->Eq($other)) {
 61         $cont->Cont($qenv, $fail);
 62     } else {
 63         $fail->Fail();
 64     }
 65 }

This works for all atomic data types. If the two patterns are Eq() then succeed, otherwise fail. This is the first place we've actually seen the failure continuation invoked. Note that the equality test Eq() implicitly deals with type equivalence for us, so we don't need the arrays() routines etc. from the prototype. Now the only other place we need to put UnifyType() is in PScm::Expr::List::Pair

276 sub UnifyType {
277     my ($self, $other, $qenv, $cont, $fail) = @_;
278     if ($other->is_pair) {
279         $self->[FIRST]->Unify(
280             $other->[FIRST],
281             $qenv,
282             cont {
283                 my ($qenv, $fail) = @_;
284                 $self->[REST]->Unify(
285                     $other->[REST],
286                     $qenv,
287                     $cont,
288                     $fail
289                 );
290             },
291             $fail
292         );
293     } else {
294         $fail->Fail();
295     }
296 }

This PScm::Expr::List::Pair::UnifyType() is in fact simpler in one sense than the unify_arrays() from our test implementation. First it performs a simple check that the $other is a list. If not it calls the failure continuation. Then, rather than walking both lists, it only needs to call Unify() on its first() and rest(), passing the $other's first() or rest() appropriately. Of course this is a little complicated because it's in CPS, but nonetheless that is all it has to do.

---

That's all for unify itself. If you remember from the start of this section, we will also need a substitute builtin to replace pattern variables with values in the environment. It is called like (substitute ‹pattern› ‹env›) and returns the ‹pattern› suitably instantiated. We can make this a primitive rather than a special form because it has no need of an environment (other than the one that is explicitly passed) and no need to access the failure continuation (it always succeeds). Here's PScm::Primitive::Substitute:

216 package PScm::Primitive::Substitute;
217 
218 use base qw(PScm::Primitive);
219 
220 sub _apply {
221     my ($self, $body, $qenv) = @_;
222     $body->Substitute($qenv->ResolveAll());
223 }

It does nothing much by itself, merely calling a ResolveAll() method on the argument environment then passing the result to the $body's Substitute() method. We'll take a look at that new PScm::Env::ResolveAll() method first.

266 sub ResolveAll {
267     my ($self) = @_;
268     my %bindings;
269     foreach my $var ($self->Keys) {
270         $bindings{$var} = $self->Resolve(new PScm::Expr::Var($var));
271     }
272     return $self->new(%bindings);
273 }

This ResolveAll() loops over each key in the environment, calling a subsidary Resolve() method on each and saving the result in a temporary %bindings hash. Then it creates and returns a new PScm::Env with those bindings.

If you refer back to our resolve() function in the prototype, you can see that in the first stage, if the $pattern is a variable, it repeatedly attempts to replace it with a value from the environment until either it is not a variable anymore or it cannot find a value. This ResolveAll() is effectively pre-processing the environment so that any subsequent lookup for a pattern variable will not need to perform that iteration.

Keys() just collects all the keys from the environment:

275 sub Keys {
276     my ($self, $seen) = @_;
277     $seen ||= {};
278     foreach my $key (keys %{$self->{bindings}}) {
279         $seen->{$key} = 1;
280     }
281     if ($self->{parent}) {
282         $self->{parent}->Keys($seen);
283     }
284     return (keys %$seen);
285 }

and Resolve() does exactly what resolve() did in our test implementation: it repeatedly replaces the variable with its value from the environment until the variable is not a variable any more, or cannot be found. If it finds a non-variable value it calls its ResolveTerm() method on it, passing the env $self as argument, and returning the result.

287 sub Resolve {
288     my ($self, $term) = @_;
289     while ($term->is_var) {
290         if (my $val = $self->LookUpNoError($term)) {
291             $term = $val;
292         } else {
293             return $term;
294         }
295     }
296     return $term->ResolveTerm($self);
297 }

ResolveTerm() gives any compound term a chance to resolve any pattern variables it may contain. There are two definitions of ResolveTerm(). The only compound terms in PScheme are lists, and pattern variables themselves have already been resolved, so the default ResolveTerm() in PScm::Expr just returns $self:

 67 sub ResolveTerm {
 68     my ($self, $qenv) = @_;
 69     return $self;
 70 }

The second definition of ResolveTerm() is, not surprisingly, in PScm::Expr::List::Pair:

298 sub ResolveTerm {
299     my ($self, $qenv) = @_;
300     return $self->Cons($qenv->Resolve($self->[FIRST]),
301                        $qenv->Resolve($self->[REST]));
302 }

It walks itself, calling the argument $qenv's Resolve() method on each component, and returning a new PScm::Expr::List of the results.

So we're talking about how substitute works, and we saw that primitive's _apply() method called the argument $qenv's ResolveAll() method to return a new environment with any pattern variables in the values replaced, where possible. Then _apply() passed that new environment to its argument $body's Substitute() method. We've just seen how ResolveAll() works, now we can look at Substitute() itself.

Only pattern variables can be substituted, but lists need to examine themselves to see if they contain any pattern variables. So a default Substitute() method in PScm::Expr takes care of all the things that can't be substituted, it just returns $self:

 72 sub Substitute {
 73     my ($self, $qenv) = @_;
 74     return $self;
 75 }

The Substitute() in PScm::Expr::Var returns either its value from the environment or itself if it is not in the environment:

405 sub Substitute {
406     my ($self, $qenv) = @_;
407     return $qenv->LookUpNoError($self) || $self;
408 }

Finally, the Substitute() in PScm::Expr::List::Pair recursively calls Substitute() on each of its components, constructing a new list of the results:

304 sub Substitute {
305     my ($self, $qenv) = @_;
306     return $self->Cons($self->[FIRST]->Substitute($qenv),
307                        $self->[REST]->Substitute($qenv));
308 }

And that's substitute. To sum up, it tries as hard as it can to replace all pattern variables in the form with values from the environment, recursing not only into the form it is substituting, but also into the values of the variables themselves.

---

There are a few more things we need to add to the interpreter before we can show off its new prowess. Firstly we will have occasion to pass an empty environment into unify (indirectly), and for that we'll need a new-env primitive. This is as simple as it gets:

258 package PScm::Primitive::NewEnv;
259 
260 use base qw(PScm::Primitive);
261 
262 sub _apply {
263     new PScm::Env();
264 }

---

Another thing we'll need goes back to a passing comment I made a while back. It can be a problem if you try to unify two patterns that inadvertantly use the same pattern variable names. Sometimes you want the variables to share a value, and sometimes you don't. For this reason we need something that will take a pattern and replace its variable names with new variable names that are guaranteed to be unique. The same variable occurring more than once in the pattern should correspond to the same new variable occurring more than once in the result, but we should be reasonably confident that the new variable name won't appear anywhere else in the program by accident.

This new PScheme function is called instantiate. It could be written in the PScheme language, but that would require adding other less germane primitives for creating symbols etc. so all in all it is probably better to build it in to the core. It can be a primitive, but it will need a bit more than just an _apply() method:

267 package PScm::Primitive::Instantiate;
268 
269 use base qw(PScm::Primitive);
270 
271 sub new {
272     my ($class) = @_;
273     bless {
274         seen => {},
275         counter => 0,
276     }, $class;
277 }
278 
279 sub _apply {
280     my ($self, $body) = @_;
281     $self->{seen} = {};
282     $body->Instantiate($self);
283 }
284 
285 sub Replace {
286     my ($self, $var) = @_;
287     return $var if $var->is_anon;
288     unless (exists($self->{seen}{$var->value})) {
289         $self->{seen}{$var->value} =
290             new PScm::Expr::Var($self->{counter}++);
291     }
292     return $self->{seen}{$var->value};
293 }
294 
295 1;

Remember that there is only one instance of any given primitive or special form in the PScheme environment, and that persists for the duration of the repl. So by giving this primitive its own new() method we provide a convenient place to store a singleton counter that we can use to generate new symbols. The seen field of the object however, which keeps track of which variables the instantiate function has already encountered, must be re-initialized to an empty hash on each separate application of the primitive. After (re-)initializing seen on Line 281, _apply() calls its argument $body's Instantiate() method passing $self as argument.

Obviously the only PScm::Expr type that will avail itself of the instantiate object is PScm::Expr::Var, and that will make use of the callback method Replace() to find or generate a replacement variable. Replace() then, first checks to see if the variable is the anonymous variable (Line 287). If so then it just returns the variable, since the anonymous variable never shares and should never be replaced by a variable that will share. Then unless it has already seen the variable it creates a new alias for it by using the incrementing counter (Lines 288–291). This works well because the reader would never create a PScm::Expr::Var from a number.

Just as with Unify() and Substitute(), a default method Instantiate() in PScm::Expr handles most cases and just returns $self:

 79 sub Instantiate {
 80     my ($self, $instantiator) = @_;
 81     return $self;
 82 }

The PScm::Expr::Var version of instantiate calls the $instantiator's Replace() callback to get a new variable, passing $self as argument because Replace() needs to keep track of the variables it has seen already:

412 sub Instantiate {
413     my ($self, $instantiator) = @_;
414     return $instantiator->Replace($self);
415 }

Finally PScm::Expr::List::Pair::Instantiate() recurses on both its first() and rest() components, calling Instantiate() on both and constructing a new list on the way back out:

316 sub Instantiate {
317     my ($self, $instantiator) = @_;
318     return $self->Cons($self->[FIRST]->Instantiate($instantiator),
319                        $self->[REST]->Instantiate($instantiator));
320 }

---

The last thing we're going to need, for pragmatic reasons, is a way to check the type of various expressions from within the PScheme language. A proper scheme implementation has a full set of such type checking functions, but we're only going to need pair?, number? and var? (note the question marks.) They are all primitives, and in fact have so much in common that we will create an abstract parent class called PScm::Primitive::TypeCheck and put a shared _apply() method in there:

226 package PScm::Primitive::TypeCheck;
227 
228 use base qw(PScm::Primitive);
229 
230 sub _apply {
231     my ($self, $body) = @_;
232     if ($self->test($body)) {
233         return new PScm::Expr::Number(1);
234     } else {
235         return new PScm::Expr::Number(0);
236     }
237 }

You can see that it calls a test() method which we must subclass for each test, then it returns an appropriate true or false value depending on the test. Here's the test for pair? in PScm::Primitive::TypeCheck::Pair:

240 package PScm::Primitive::TypeCheck::Pair;
241 use base qw(PScm::Primitive::TypeCheck);
242 
243 sub test { $_[1]->is_pair }

We've already seen that is_pair() is defined false in PScm::Expr and overridden to be true in PScm::Expr::List::Pair alone. The equivalent number? and var? PScheme functions are bound to PScm::Primitive::TypeCheck::Number and PScm::Primitive::TypeCheck::Var, and make use of equivalent is_number() and is_var() methods in PScm::Expr.

---

We have now implemented the four components we need to get on with defining a logic programming language: unify, substitute, new-env and instantiate. Along with those we have also added the three type tests pair?, var? and number? which just check if their argument is of that type. They are all wired in to the repl in the normal way, here's the additions:

 36 sub ReadEvalPrint {
 37     my ($infh, $outfh) = @_;
 38 
 39     $outfh ||= new FileHandle(">-");
 40     my $reader      = new PScm::Read($infh);
 41     my $initial_env;
 42     $initial_env = new PScm::Env(
 43         let          => new PScm::SpecialForm::Let(),
 44         '*'          => new PScm::Primitive::Multiply(),
 45         '-'          => new PScm::Primitive::Subtract(),
 46         '+'          => new PScm::Primitive::Add(),
 47         if           => new PScm::SpecialForm::If(),
 48         lambda       => new PScm::SpecialForm::Lambda(),
 49         list         => new PScm::Primitive::List(),
 50         car          => new PScm::Primitive::Car(),
 51         cdr          => new PScm::Primitive::Cdr(),
 52         cons         => new PScm::Primitive::Cons(),
 53         letrec       => new PScm::SpecialForm::LetRec(),
 54         'let*'       => new PScm::SpecialForm::LetStar(),
 55         eval         => new PScm::SpecialForm::Eval(),
 56         macro        => new PScm::SpecialForm::Macro(),
 57         quote        => new PScm::SpecialForm::Quote(),
 58         'set!'       => new PScm::SpecialForm::Set(),
 59         begin        => new PScm::SpecialForm::Begin(),
 60         define       => new PScm::SpecialForm::Define(),
 61         'make-class' => new PScm::SpecialForm::MakeClass(),
 62         'call/cc'    => new PScm::SpecialForm::CallCC(),
 63         print        => new PScm::SpecialForm::Print($outfh),
 64         spawn        => new PScm::SpecialForm::Spawn(),
 65         exit         => new PScm::SpecialForm::Exit(),
 66         error        => new PScm::SpecialForm::Error(
 67                         $outfh,
 68                         bounce { repl($initial_env, $reader, $outfh) }
 69                      ),
 70         amb          => new PScm::SpecialForm::Amb(),
 71         'eq?'        => new PScm::Primitive::Eq(),
 72         '>'          => new PScm::Primitive::Gt(),
 73         '<'          => new PScm::Primitive::Lt(),
 74         '>='         => new PScm::Primitive::Ge(),
 75         '<='         => new PScm::Primitive::Le(),
 76         and          => new PScm::SpecialForm::And(),
 77         or           => new PScm::SpecialForm::Or(),
 78         unify        => new PScm::SpecialForm::Unify(),
 79         substitute   => new PScm::Primitive::Substitute(),
 80         'new-env'    => new PScm::Primitive::NewEnv(),
 81         instantiate  => new PScm::Primitive::Instantiate(),
 82         'pair?'      => new PScm::Primitive::TypeCheck::Pair(),
 83         'var?'       => new PScm::Primitive::TypeCheck::Var(),
 84         'number?'    => new PScm::Primitive::TypeCheck::Number(),
 85     );
 86 
 87     $initial_env->Define(
 88         PScm::Expr::Symbol->new("root"),
 89         PScm::Class::Root->new($initial_env)
 90     );
 91     __PACKAGE__->new_thread(bounce { repl($initial_env, $reader, $outfh) });
 92     trampoline();
 93 }

17.5.1. Parsing (again)

We saw in Section 16.2.4 that amb by itself was very useful for parsing because of its built in backtracking capability. However combining amb with unification as we have done here makes parsing an extraordinarily simple task, at least if we are prepared to accept the accompanying inefficiencies.

Consider the following rules for parsing a set of sentences worked through in the tests from Chapter 16, Listing 32. This is a different set of sentences to those worked through in Section 16.2.4, the sentences in question are:

• “John will put his car in the garage.”
• “Paul put a car in his garage.”
• “Paul has put a very very old car in his quite new red garage.”

These are obviously more complex than the sentences we worked through with amb, but we can deal with them easily enough here:

(define the-rules
  (list
        '((proper-noun (john)))
        '((proper-noun (paul)))
        '((noun (car)))
        '((noun (garage)))
        '((auxilliary (will)))
        '((auxilliary (has)))
        '((verb (put)))
        '((article (the)))
        '((article (a)))
        '((article (his)))
        '((preposition (in)))
        '((preposition (to)))
        '((preposition (with)))
        '((degree (very)))
        '((degree (quite)))
        '((adjective (red)))
        '((adjective (green)))
        '((adjective (old)))
        '((adjective (new)))

        '((append () Y Y))
        '((append (A . X) Y (A . Z)) (append X Y Z))

        '((sentence S)
            (append NP VP S)
            (noun-phrase NP) (verb-phrase VP))
        '((sentence S)
            (append _X VP S) (append NP AUX _X)
            (noun-phrase NP) (auxilliary AUX) (verb-phrase VP))

        '((noun-phrase NP)
            (append ART ADJP NP)
            (article ART) (adj-phrase ADJP))
        '((noun-phrase NP) (proper-noun NP))

        '((adj-phrase ADJP) (noun ADJP))
        '((adj-phrase ADJP)
            (append DGP ADJP2 ADJP)
            (degree-phrase DGP) (adj-phrase ADJP2))

        '((degree-phrase DGP) (adjective DGP))
        '((deg-phrase DGP)
            (append DEG DGP2 DGP)
            (degree DEG) (deg-phrase DGP2))

        '((verb-phrase VP)
            (append _X PP VP) (append VB NP _X)
            (verb VB) (noun-phrase NP) (prep-phrase PP))

        '((prep-phrase PP)
            (append PR NP PP)
            (preposition PR) (noun-phrase NP))))
[download]

This is little more than a declaration of the rules of the grammar. Let's look at a few of those rules a little more closely.

'((adj-phrase ADJP) (noun ADJP))
'((adj-phrase ADJP)
    (append DGP ADJP2 ADJP)
    (degree-phrase DGP) (adj-phrase ADJP2))
[download]

This rule about adjectival phrases is in two parts. The first part says that ADJP is an adj-phrase if ADJP is a noun. The second part says ADJP is an adj-phrase if some DGP and ADJP2 append to form ADJP, and DGP is a degree-phrase, and ADJP2 is an adj-phrase.

'((noun (car)))
'((noun (garage)))
[download]

This pair of rules defines the nouns we know about. They say (car) is a noun and (garage) is a noun. The nouns themselves are in lists because the system deals with lists: consider the adj-phrase rules above, where ADJP must be a list for append to work on it.

Given the above, we can ask the obvious question:

> (prove '((sentence (john put his car in the garage))))
((sentence (john put his car in the garage)))
[download]

You get the desired response, eventually⁵⁹. Interestingly, you can also ask it “what is a sentence”:

> (prove '((sentence S)))
((sentence (john put john in the car)))
> ?
((sentence (john put john in the garage)))
> ?
((sentence (john put john in the red car)))
> ?
((sentence (john put john in the red garage)))
> ?
((sentence (john put john in the red red car)))
> ?
((sentence (john put john in the red red garage)))
> ?
((sentence (john put john in the red red red car)))
[download]

It gets stuck in a recursive rut after a while, but it's exciting to see that it has the potential to generate all sentences of a grammar if it could avoid those traps⁶⁰. However that's not the real problem, the real problem is that it is horribly inefficient. All of those calls to append, most of which produce useless results, consume huge amounts of resources.

However we can take a hint from the way that we implemented parsing with amb in Section 16.2.4. In that implementation, the routine parse-word removed tokens from the front of the *unparsed* global, effectively “directing” the progress of the parse, since it exposed the next token and only certain words would match that newly exposed token. We can't use “global variables” in a logic programming system—the concept has no meaning—but we can nonetheless keep track of what has been parsed so far.

We can do this by making all of our grammar rules take a second argument. For example:

(noun-phrase S R)
[download]

Will succeed if there is a noun phrase at the start of S, and if R is the remainder of S after removing that noun phrase. Perhaps this approach is most easily demonstrated for individual words. Here's the new definition of noun:

'((noun (car . S) S))
'((noun (garage . S) S))
[download]

It will match if its first argument is a list starting with car or garage, an in the process instantiate its second argument to the remainder of the list. For example:

> (prove '((noun (garage is red) X)))
((noun (garage is red) (is red)))
[download]

If we write the other rules for single words similarily, we can start to build up more complex rules on top:

'((noun-phrase S X)
    (article S S1) (adj-phrase S1 X))
[download]

This says that there is a noun phrase at the start of S, leaving X remaining if there is an article at the start of S leaving S1 remaining, and an adjectival phrase at the start of S1, leaving X remaining. Note that we no longer need to use append to “generate and test”. We can further build on these intermediate rules just as with the previous grammar:

'((sentence S X)
    (noun-phrase S S1) (verb-phrase S1 X))
[download]

In order to use this new parser, we must remember to pass an empty list as the second argument to sentence, to ensure that all of the tokens in the first argument are consumed:

> (prove '((sentence (john put his car in the garage) ())))
((sentence (john put his car in the garage) ()))
[download]

Putting all of this together, we can see the considerably faster (but uglier) version in the test at the end of Listing 34.

Ugliness is not just an aesthetic thing, it gets in the way of clear and readable code. For that reason any full Prolog implementation provides rewriting rules that will accept a simple grammar with statements like⁶¹:

(sentence --> noun-phrase verb-phrase)
[download]

It will transform them into the internal form:

((sentence X0 X1) (noun-phrase X0 X2) (verb-phrase X2 X1))
[download]

as it reads them in. I'm not going to do that, since it would require generating symbols etc. but it should be obvious that this sort of transformation is not difficult.

17.5.2. Simplifying Algebraic Expressions

If you remember back in Section 17.1.5 The result of differentiating the expression (((x ^ 2) + x) + 1) was (((2 * (x ^ 1)) + 1) + 0). While correct, this is somewhat unwieldy as it contains redundant operations such as the addition of zero. It is relatively easy to write a set of rules that can automatically simplify such expressions, however we have to be careful of the order in which we specify the rules. This is not only a feature of our implementation, the order of the rules, which is the order in which they will be searched, is significant in Prolog too.

We start off by saying that we cannot simplify anything unless it has some internal structure:

'((simplify E E) (require (not (pair? 'E))))
[download]

So if E is not a pair, then it will simplify to itself.

We next get to the main driver rule for simplification:

'((simplify (X OP Y) E)
    (simplify X X1)
    (simplify Y Y1)
    (s (X1 OP Y1) E))
[download]

This says that we can simplify an expression of the form (X OP Y) to E if

1. we can simplify X to X1;
2. we can simplify Y to Y1;
3. we can simplify (X1 OP Y1) to E using the auxilliary simplification rules (s (‹E1› ‹OP› ‹E2›) ‹E3›).

These auxilliary simplification rules occupy the rest of the definition of simplification. Firstly here are the rules for addition:

'((s (X + 0) X))
'((s (0 + X) X))
'((s (X + Y) Z)
    (require (and (number? 'X) (number? 'Y)))
    (Z is (+ X Y)))
'((s (X + Y) (X + Y)))
[download]

The first rule says that X plus zero is just X. The second rule is a necessary repetition of the first, reversing 0 and X. The third rule says that we can simplify (X + Y) to Z if X and Y are both numbers, by making Z equal to their sum. The last rule is there in case the term can not be simplified, in which case the result is just the original.

The rules for simplifying multiplication are very similar, except that we can simplify both multiplication by zero and multiplication by one:

'((s (X * 0) 0))
'((s (0 * X) 0))
'((s (X * 1) X))
'((s (1 * X) X))
'((s (X * Y) Z)
    (require (and (number? 'X) (number? 'Y)))
    (Z is (* X Y)))
'((s (X * Y) (X * Y)))
[download]

Likewise for exponentiation, except that we don't have a “^” operator in PScheme so we can't perform any actual numeric computation in this case:

'((s (X ^ 0) 1))
'((s (X ^ 1) X))
'((s (X ^ Y) (X ^ Y)))))
[download]

With these rules in place we can ask the system to simplify that unwieldy expression we saw before:

> (prove '((simplify (((2 * (x ^ 1)) + 1) + 0) X)))
((simplify (((2 * (x ^ 1)) + 1) + 0) ((2 * x) + 1)))
[download]

Note that these rules for simplification are very incomplete, most noticeably they do not deal with subtraction or division. However they are sufficient to demonstrate that they work and you can add the extra rules yourself if you want to extend or experiment (this example is part of the tests in Listing 34.)

17.6.1. Functors and Arity

In Prolog, facts and rules are not defined as simple lists. Prolog distinguishes between the functor of a rule and its arguments. For example the PScheme “fact”:

((mary likes cheese))
[download]

would be written in Prolog as:

likes(mary, cheese).
[download]

and the rule:

((likes mary X) (person X) (X likes chips))
[download]

would be written as:

likes(mary, X) :- person(X), likes(X, chips).
[download]

In this example likes is called the functor of the rule. Because it takes two arguments, it is said to have an arity of 2, and is classified as likes/2. This is distinct from any likes functor with a different number of arguments, Just as in our implementation lists of different length cannot match.

The big advantage in distinguishing functor/arity like this is that Prolog can index its database on this basis. Unification is expensive, so when searching for a rule to match i.e. likes(mary, X) Prolog need only inspect rules that are likes/2.

Of course this means that the functor cannot be matched by a pattern variable. The expression:

X(mary, wine)
[download]

is not valid Prolog. However Prolog has mechanisms to extract the functor from a term as a variable, and to call an expression constructed with a variable functor, so this apparent limitation can be worked around.

Prolog also recognises operators and operator precedence, such that the normal mathematical operators are infix and are parsed with the correct precedence and associativity. Prolog operators are functors, so for example the form:

a + b * c
[download]

is equivalent to:

+(a, *(b, c))
[download]

Prolog also allows you to define new operators as any sequence of non-alphanumeric characters, and assign them a precedence and associativity. These user defined operators don't actually do anything: they just make it easier to write Prolog terms as they translate internally to normal functors just as the built-in operators do.

17.6.2. The Cut

Another reason that Prolog distinguishes its functors is to allow short circuiting of the search space. Prolog provides a special rule called the cut to accomplish this [pip pp69–92]. The cut is written with a single exclaimation mark “!”. As part of the body of a rule, the cut always succeeds. But if it is backtracked through, it backtracks all the way past the point where the head of the rule was unified, and past the point where rules of that functor/arity were considered, back to the decision point before that. This is extremely useful behaviour.

For example, returning to our simplify example of algebraic simplification from Section 17.5.2, our very first rule was:

'((simplify E E) (require (not (pair? 'E))))
[download]

This was saying that you can simplify E to E if E is not a pair (is atomic.) We might translate this into Prolog as:

simplify(E, E) :- atomic(E).
[download]

However this is better expressed in Prolog as:

simplify(E, E) :- atomic(E), !.
[download]

This says that if this rule succeeds, then no other simplify/2 rules should be considered if backtracking occurs through the cut. If the expression E is atomic, then it cannot be simplified, end of story.

There are other uses of the cut, but they are best described in a book on Prolog.

In order to properly implement the cut, we would have to pass a third cut{} continuation around, which makes the Parameter Object pattern discussed in Section 16.5.1 even more attractive.

17.6.3. Backtracking Efficiency

As I've already mentioned in Section 16.5, the chronological backtracking exhibited by amb is hopelessly inefficient, and an alternative dependancy-directed backtracking is preferable. This kind of backtracking examines the cause of any failure, and backtracks immediately to the point of execution that most recently affected the failure. Dependancy directed backtracking is often implemented by a constraint network, which allows the backtracking to proceed directly to the last place that the value in question was altered. Again this is beyond the scope of this book⁶².