Understanding this chapter relies heavily on previous chapters.
If you have skipped ahead to here, you should at least make sure
that you understand the implementation details of CPS
from Chapter 13 before diving in to the
details that follow. However
you can read the next few sections on their own if you want to get a taste
of what this chapter has to offer.
16.1. Introducing amb
The feature we shall be adding is called amb [sicp pp412–437].
amb is short for “ambivalent”—in
the sense of “having more than one value”.
As I've said it is best introduced by example, and the
simplest example is this:
> (amb 1 2 3)
1
> ?
2
> ?
3
> ?
Error: no more solutions
> ?
Error: no current problem
What's going on here? Well amb is given a list of
values, and returns all of them. But it returns them one at a time.
When a “?” is typed at the
PScheme prompt control backtracks to amb and it returns its
next result.
So the execution of expressions involving amb is somehow
threaded into the read-eval-print loop itself. I should probably
point out that this new behaviour is not specific to amb,
but rather a general property of the interpreter:
> ?
Error: no current problem
> (+ 2 2)
4
> ?
Error: no more solutions
> ?
Error: no current problem
The Error: no current problem message means just that:
there is no current problem so no backtracking is possible, wheras the
Error: no more solutions message means that the current
“problem” has just exhahsted all of its posibilities. With
no occurence of amb in the “problem” there is only one
possible outcome (4 in the (+ 2 2) example above) so the repl
continues to behave as normal for “normal” input.
amb will only return a subsequent value if it is told that the
previous value is not acceptable. One way of doing that, as we have seen,
is by typing “?” at the scheme prompt. We can do
the same thing within our code however, as I'll demonstrate next:
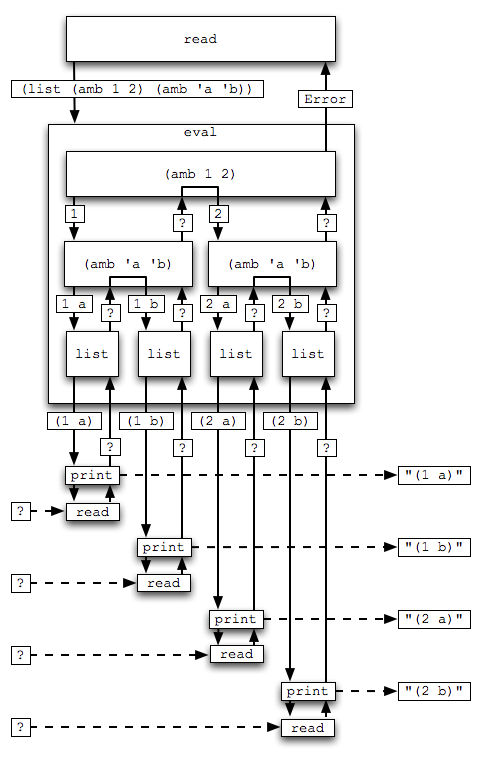
> (list (amb 1 2) (amb 'a 'b))
(1 a)
> ?
(1 b)
> ?
(2 a)
> ?
(2 b)
> ?
Error: no more solutions
Now that's interesting. There are two calls to
amb, and list collects the results.
Best we go through this one step at a time.
-
The expression first
returns a list of the first arguments to each call to
amb, namely 1 and a.
-
When we tell
the interpreter that we'd like to see more results by typing
? at the prompt, the second amb call intercepts
the request and returns its second argument, so the whole expression
returns (1 b).
-
When we ask for a third result, the second
amb again intercepts the request, but this time it has
run out of arguments, so it fails to satisfy the request and control
propogates back to the first call to amb. The
first amb now returns its second result, 2,
and control passes forwards again to the second amb.
This second amb is now being called afresh, as it were,
and is back in its initial state where it returns its first argument,
so the whole third result is (2 a).
-
The request for a
fourth result proceeds as the request for the second result did,
with the second
amb producing b, resulting
in (2 b).
-
With the fifth and final
request, the second
amb again fails,
so propogates the failure back to the first amb, but
this time the first amb has also exhausted its results,
so propogates the failure back to the command loop and we get the
“error”.
The diagram in Figure 16.1 attempts to show this control
flow in action.
So in what way does this demonstrate that we can control the backtracking
behaviour of amb? Simple. When amb itself fails it propogates control
back to the chronologically previous call to amb, just as
typing a “?” at the prompt does.
When the second amb call ran out of options in the example, control
propogated back to the first amb call.
Now a call to amb
with no arguments must immediately fail, because it has no arguments to
choose from:
> (amb)
Error: no more solutions
So calling amb with no arguments forces any previous amb to
deliver up its next value. We can wrap that behaviour in a function
that tests some condition, and forces another choice if the condition
is false. That function is called require:
(define require
(lambda (x)
(if x x (amb))))
The return value of x if the test succeeds is merely utilitarian,
it is the call to amb with no arguments if the test fails that is important.
So how can we use requre? Well for example let's assume we have a
predicate even? that returns true if its argument
is even. We can use that to filter the results of an earlier amb:
> (let ((x (amb 1 2 3 4 5 6)))
> (begin
> (require (even? x))
> x))
2
> ?
4
> ?
6
> ?
Error: no more solutions
The expression (require (even? x)) filtered out the odd values of
x, so only the even values were propogated to the result(s)
of the expression.
You should be starting to see
how amb and CPS are deeply interlinked, and how backtracking
can therefore return to any chronologically previous
point in the computation, not just “down the stack” to
a caller of the code that initiates the backtracking.
16.2. Examples of amb in Action
Now we know what amb does, what can we use it for?
That example with (require even? x) above
should give you some idea, but
in a word: search.
16.2.1. The “Liars” Puzzle
Consider the following logic problem, one of
a classic and simple type.
Liars
Five schoolgirls sat for an examination. Their
parents—so they thought—showed
an undue degree of interest in the result. They therefore
agreed that, in writing home about the examination, each girl should
make one true statement and one untrue one. The following are the
relevant passages from their letters:
- Betty:
- “Kitty was second in the examination, I was only third.”
- Ethel:
- “You'll be glad to hear that I was on top. Joan was second.”
- Joan:
- “I was third, and poor old Ethel was bottom.”
- Kitty:
- “I came out second. Mary was only fourth.”
- Mary:
- “I was fourth. Top place was taken by Betty.”
What in fact was the order in which the five girls were placed?
amb makes it easy to solve this type of problem by
merely enumerating all the possibilities then eliminating
those possibilities that are wrong in some way:
> (define liars
> (lambda ()
> (let ((betty (amb 1 2 3 4 5))
> (ethel (amb 1 2 3 4 5))
> (joan (amb 1 2 3 4 5))
> (kitty (amb 1 2 3 4 5))
> (mary (amb 1 2 3 4 5)))
> (begin
> (require (distinct? (list betty ethel joan kitty mary)))
> (require (xor (eq? kitty 2) (eq? betty 3)))
> (require (xor (eq? ethel 1) (eq? joan 2)))
> (require (xor (eq? joan 3) (eq? ethel 5)))
> (require (xor (eq? kitty 2) (eq? mary 4)))
> (require (xor (eq? mary 4) (eq? betty 1)))
> '((betty ,betty)
> (ethel ,ethel)
> (joan ,joan)
> (kitty ,kitty)
> (mary ,mary))))))
liars
> (liars)
((betty 3) (ethel 5) (joan 2) (kitty 1) (mary 4))
The bindings in the let supply all possible grades to each
of the girls, then the first require in the body of the
let makes sure that all the girls have different grades:
the distinct? function only returns true if there are no
duplicates in its argument list. I'll show you the implementation,
and that of other functions here, later. The remaining requirements
simply list the two parts of each girl's statement, requiring that
one is true and one is false:
the xor (exclusive
or) function returns true only if one of its arguments is true and
the other is false. The eq? function tests if two expressions
are equal.
So we start out by requiring that all five girls have distinct
positions in the exam results. The we go on to require that exactly
one of each of the girls two statements is true. Finally we build and
return a list of pairs of the girl's names, and the associated positions that
satisfy all the requirements, using quote and
unquote.
Of course this is horribly inefficient. There are
55 = 3125
permutations of
betty,
ethel,
joan,
kitty and
mary, and that first distinct requirement
forces a re-evaluation of all but 5! = 120 of them,
so about 96% of the initial possibilities are pruned at the first
step, and backtracking is provoked. In fact, when writing tests for
this amb example, this single function took so long to run
(about 14 seconds on my laptop) that I was forced
to find ways to optimize it. The optimizations demonstrate some
additional behaviour of amb, so here's the optimized version:
(define liars
(lambda ()
(let* ((betty (amb 1 2 3 4 5))
(ethel (one-of (exclude (list betty)
(list 1 2 3 4 5))))
(joan (one-of (exclude (list betty ethel)
(list 1 2 3 4 5))))
(kitty (one-of (exclude (list betty ethel joan)
(list 1 2 3 4 5))))
(mary (car (exclude (list betty ethel joan kitty)
(list 1 2 3 4 5)))))
(begin
(require (xor (eq? kitty 2) (eq? betty 3)))
(require (xor (eq? ethel 1) (eq? joan 2)))
(require (xor (eq? joan 3) (eq? ethel 5)))
(require (xor (eq? kitty 2) (eq? mary 4)))
(require (xor (eq? mary 4) (eq? betty 1)))
'((betty ,betty)
(ethel ,ethel)
(joan ,joan)
(kitty ,kitty)
(mary ,mary))))))
It starts out as before, setting betty to an amb
choice from the available positions, but then calls a couple
of new functions to calculate the value for ethel
and the rest of the girls.
exclude returns a list of all the elements in
its second list that aren't in its first list. So for example
if betty is 1, then ethel
only gets the choice of values 2 through 5.
I'll show you exclude
later. one-of is more interesting, since it makes use
of require and amb. It does the same thing as amb,
but takes a single list of values as argument rather than
individual arguments:
(define one-of
(lambda (lst)
(begin
(require lst)
(amb (car lst) (one-of (cdr lst))))))
Firstly it requires that the list is not empty, then it uses
amb to choose
either the car of the list, or one-of the cdr of
the list. This in fact demonstrates that amb must be a special
form: this function would not work if amb had its arguments
evaluated for it; if both arguments to that second amb were
evaluated before amb saw them then one-of would
get recursively executed until the list was empty,
then the first amb to be actually invoked would be
the one that terminates recursion when (require lst)
fails, so this function would always fail if
amb were a primitive.
Back to our optimized liars example. The use
of let* instead of let makes the values of the previous
bindings available to subsequent ones. By the time we get to assigning
to mary, there is only one choice left, so we just take
it with car rather than using one-of. Since our values are now
guaranteed to be distinct, we can remove that explicit requirement
from the code, and the optimized version runs in a little under
a second on the same machine.
As promised, here are the rest of the scheme functions needed
to implement the solution to the “Liars” puzzle and other
examples seen earlier. You can
skim these if you're not interested in the details, they don't
really do anything new.
To make these functions easier to write (and read) I've introduced
the boolean short circuiting special forms and and
or to this version of the interpreter: (and a b)
will return a without evaluating b if a
is false, and (or a b) will return a without evaluating
b if a is true.
Some of these functions also make use of not.
and and or have been added as special forms
to the interpreter and so interact with the amb rewrite,
so you'll have to wait to see those,
but not is just:
(define not
(lambda (x)
(if x 0 1)))
And so to our support routines. Firstly even?:
(define divisible-by
(lambda (n)
(lambda (v)
(begin
(define loop
(lambda (o)
(if (eq? o v)
1
(if (> o v)
0
(loop (+ o n))))))
(loop 0)))))
(define even?
(lambda (a)
((divisible-by 2) a)))
This is really just demonstrating the functional programming
style that Scheme promotes.
The function divisible-by
takes an argument number n and returns another function that
will return true if its argument is divisible by n.
It creates an inner loop method which loops over 0,
n, 2n, 3n ... until either
equal to or greater than the number being tested.
even? uses this to create a function that tests
for divisibility by 2, and calls it on its argument a.
It is total overkill to do it this way, but fun.
Next distinct?:
(define distinct?
(lambda (lst)
(if lst
(and (not (member? (car lst) (cdr lst)))
(distinct? (cdr lst)))
1)))
distinct? says
if the list is not empty, then it is distinct if its first
element (its car) is not a member of the rest of the list
and the rest of the list is distinct. If the list is empty,
then it is distinct. distinct makes use of another
function, member?, shown next.
(define member?
(lambda (item lst)
(if lst
(or (eq? item (car lst))
(member? item (cdr lst)))
0)))
member? determines if its argument item
is a member of its argument lst. It says if the list is not empty,
then the item is a member of the list if it is equal to the
car of the list or a member of the cdr of the list. The item
is not a member of an empty list. member? uses
another function eq? to test equality, but that's
been added to the interpreter as a primitive, so we'll leave that
for later.
Next up for consideration is xor. xor
takes two arguments and returns true only if precisely one of those
arguments is false.
(define xor
(lambda (x y)
(or (and x (not y))
(and y (not x)))))
Lastly for the support routines, our optimized example made use of
exclude which returns its second argument list after removing
any items on its first argument list. It's easy to do now that we have
member?:
(define exclude
(lambda (items lst)
(if lst
(if (member? (car lst) items)
(exclude items (cdr lst))
(cons (car lst)
(exclude items (cdr lst))))
())))
For a non-empty list: if the first element is to be excluded
then just return the result of calling exclude on the
rest of the list. If it is not to be excluded, then prepend it to the
result of calling exclude on the rest of the list.
For an empty list the only result can be the empty list.
16.2.2. Barrels of Fun
Our next example is another logic puzzle, from
[mensa]. It is somewhat
different, but requires much the same approach.
Barrels of Fun
A wine merchant has six barrels of wine and beer containing:
- 30 gallons
- 32 gallons
- 36 gallons
- 38 gallons
- 40 gallons
- 62 gallons
Five barrels are filled with wine and one with beer. The first customer
purchases two barrels of wine. The second customer purchases twice
as much wine as the first customer. Which barrel contains beer?
Here's a solution:
(define barrels-of-fun
(lambda ()
(let* ((barrels (list 30 32 36 38 40 62))
(beer (one-of barrels))
(wine (exclude (list beer) barrels))
(barrel-1 (one-of wine))
(barrel-2 (one-of (exclude (list barrel-1) wine)))
(purchase (some-of (exclude (list barrel-1 barrel-2) wine))))
(begin
(require (eq? (* 2 (+ barrel-1 barrel-2))
(sum purchase)))
beer))))
Again, it is more or less just a statement of the problem.
We start off by picking the beer barrel at random. Then we
say that the wine barrels are the remaining barrels.
Next we randomly pick the first barrel of wine bought from
the wine barrels, and the second from the remaining wine barrels.
We don't know how many barrels the second customer bought, so we
merely assign some-of the remaining barrels to that
purchase. Finally in the body of the let we require that the second
customer buys twice as much wine as the first, then return the
beer barrel (the answer is 40 by the way).
We haven't seen some-of before.
It is very similar to one-of described above, and makes
direct use of amb.
(define some-of
(lambda (lst)
(begin
(require lst)
(amb (list (car lst))
(some-of (cdr lst))
(cons (car lst)
(some-of (cdr lst)))))))
It requires the list to be non-empty, then chooses between
just the first element of the list (as a list), some of the rest of the list,
or the first element prepended to some of the rest of the list. This
will eventually produce all non-empty subsets of the list.
The only other function we haven't seen before is sum.
It adds all the values in its argument list and is quite trivial:
(define sum
(lambda (lst)
(if lst
(+ (car lst)
(sum (cdr lst)))
0)))
The sum of a list is the car of the list plus the
sum of the cdr of the list. The sum of an empty
list is zero.
16.2.3. Pythagorean Triples
As another example of amb, consider generating so-called
pythagorean triples, triples of integers
x, y and z such that
x2 + y2 = z2.
This should be pretty easy.
> (define square
> (lambda (x)
> (* x x)))
square
> (define pythagorean-triples
> (lambda ()
> (let ((x (amb 1 2 3 4 5 6 7 8))
> (y (amb 1 2 3 4 5 6 7 8))
> (z (amb 1 2 3 4 5 6 7 8 9 10 11 12)))
> (begin
> (require (eq? (+ (square x)
> (square y))
> (square z)))
> '((x ,x) (y ,y) (z ,z))))))
pythagorean-triples
> (pythagorean-triples)
((x 3) (y 4) (z 5))
> ?
((x 4) (y 3) (z 5))
> ?
((x 6) (y 8) (z 10))
> ?
((x 8) (y 6) (z 10))
> ?
Error: no more solutions
And so it was. After defining square, we pick
some ranges of numbers x, y and z,
then require that the sum of the squares of x
and y equals the square of z.
Although it is simple and easy to understand,
that's a terribly naiive implementation. We just guessed the
range 1...8 for x and y
based on a fixed range 1...12 for
z. Plus the result includes duplicates: ((x 3) (y
4) (z 5)) is the same as ((x 4) (y 3) (z 5)).
Plus, the number of results is constrained by the highest value of
z, altogether not very satisfactory.
With the addition of a couple more functions, we can remedy all
of these deficiencies. Firstly, here's a function integers-between
that will ambivalently return every number between its lower bound
and its upper bound, in ascending order:
(define integers-between
(lambda (lower upper)
(begin
(require (<= lower upper))
(amb lower
(integers-between (+ lower 1) upper)))))
It begins by requiring that its lower bound is less than or
equal to its upper bound, then ambivalently returns first the lower
bound, then the result of calling itself with its lower bound
incremented by one.
Thinking about it, if we were to remove the bounds check from
integers-between it would continue to produce new integers, one at
a time, ad-infinitum, and without the bounds check
it would have no need for the upper bound argument. That realisation
gives us our second function, integers-from:
(define integers-from
(lambda (x)
(amb x
(integers-from (+ x 1)))))
This function will just carry on returning one integer after another
as long as it is backtracked to.
Given these two simple functions we can write a much more satisfactory
version of pythagorean-triples:
(define pythagorean-triples
(lambda ()
(let* ((z (integers-from 1))
(x (integers-between 1 z))
(y (integers-between x z)))
(begin
(require (eq? (+ (square x)
(square y))
(square z)))
'((x ,x) (y ,y) (z ,z))))))
It uses let* to make the value of z available
to the definition of x, and likewise the value of
x available to the definition of y, much as
in the liars puzzle above. It lets z
equal each of the positive integers in turn, then it lets x
range over the values 1 to z. Then, to avoid
duplication, it only allows y to range over the values
x to z. The rest of the implementation is
unchanged. It's a little slow, but it will continue to generate
unique pythagorean triples as long as you keep asking it for more:
> (pythagorean-triples)
((x 3) (y 4) (z 5))
> ?
((x 6) (y 8) (z 10))
> ?
((x 5) (y 12) (z 13))
> ?
((x 9) (y 12) (z 15))
> ?
((x 8) (y 15) (z 17))
> ?
((x 12) (y 16) (z 20))
> ?
((x 7) (y 24) (z 25))
> ?
...
To wrap up this section, although it should be obvious, it's
probably worth pointing out that there is a pitfall to using
amb to generate infinite sequences like this. The function
integers-from can never fail, so unless it is the
first call to amb in your program, any previous calls
to amb will never get backtracked to. This works out
pretty well for pythagorean-triples: since we need the
current value of z to constrain the values of x,
the call to integers-from had to happen first, but
even if we hadn't needed the value of z first, we would still
have to have calculated it first, otherwise any previous calls to
amb would never get a chance to yield more than their
first result. For example the following just won't work:
...
(let ((x (integers-from 1))
(y (integers-from 1))
(z (integers-from 1)))
...
The last call to integers-from to provide the value of
z, when backtracked to (by hitting “?”
or by some downstream call to amb), would just keep on
producing values, so the declarations of x and y
would never get backtracked to and never produce alternative
values.
16.2.4. Parsing Natural Language
Our last example of amb is a little different. It turns out that
amb is extremely useful for parsing. Because amb
can backtrack and is capable of trying many alternative strategies,
it is much more powerful than any simple bottom-up parser like
the one used to parse PScheme itself. In fact it is quite capable
of parsing some restricted subsets of natural language.
To understand what follows, it is essential to realise that even
set!, when backtracked through,
will have its effect undone. This is what is meant by “chronological
backtracking”: chronological backtracking really does restore
the state of the machine to a previous time, as if nothing
since the amb being backtracked to ever happened. I think
that is quite amazing.
To start the discussion on parsing, consider the following two
English sentences:
- “Time flies like an arrow.”
- “Fruit flies like a bannanna.”
Although superficially very similar, the two sentences have
radically different structures and semantics: Time, “the indefinite
continued progress of existence” is noted to always fly forward
in the manner of an arrow, wheras fruit flies of the genus
Melanogaster are known to be quite partial to bannanas.
This demonstrates quite vividly that it is in fact impossible
to correctly parse natural language without involving semantics,
and of course it is impossible to extract the semantics without
parsing; a chicken and egg problem that I hope to show amb can
neatly circumvent.
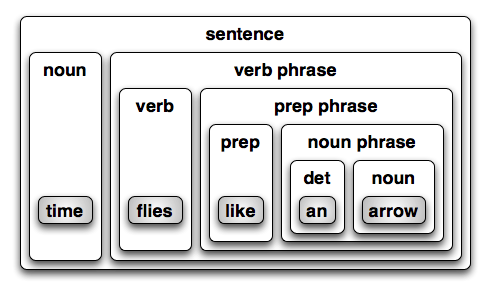
Drawing on old school grammar lessons, Figure 16.2 shows a reasonable parse tree for the first sentence. It consists
of the noun “time” and a verb phrase. The verb phrase consists
of the verb “flies” and a prepositional phrase. The prepositional
phrase consists of the preposition “like” and a noun phrase.
The noun phrase consists of the determinant “an” and the noun
“arrow”.
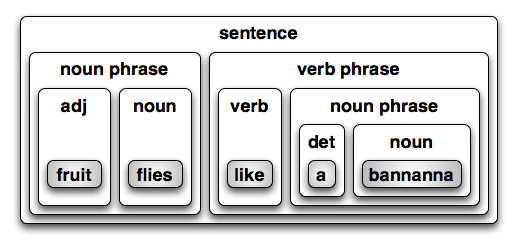
Similarily, Figure 16.3 shows a parse tree for the
second sentence. This time the sentence breaks down into the classic
noun phrase plus verb phrase structure (as did the first, but the
noun phrase just contained a noun). The noun phrase contains the
adjective “fruit” and the noun “flies”. The verb phrase
contains the verb “like” and another noun phrase. This second noun
phrase consists of the determinant “a” and the noun
“bannanna”.
In order to parse these sentences,
we can start off by categorizing the individual words:
(define verbs '(verb flies like))
(define nouns '(noun time fruit flies bannanna arrow))
(define determinants '(det a an))
(define adjectives '(adj time fruit))
(define prepositions '(prep like))
The first symbol on each list identifies the type of the rest
of the words on the list. Note that a number of the words occur
on more than one of the lists: “like” acts as a preposition
in the first sentence, while it is a verb in the second. Similarily
“flies” is the verb in the first sentence, but a noun in the
second. Additionally, I've added a couple of categorisations that
aren't needed to parse those sentences correctly, but would nonetheless
be present in a sufficiently general lexicon: “fruit” is
certainly a noun, and “time” is a perfectly acceptable adjective
(“time travel” for example). These additional classifications
are exactly what cause us to do that double take when we first
encounter these two sentences, and will make the parsing more
realistic.
Next we create a global variable *unparsed* to hold
the words remaining to be parsed. this is initially defined to be
empty:
(define *unparsed* ())
Then we define a top level parse routine:
(define parse
(lambda (input)
(begin
(set! *unparsed* input)
(let ((sentence (parse-sentence)))
(begin
(require (not *unparsed*))
sentence)))))
parse starts by setting the global *unparsed*
to its argument. Then it calls parse-sentence, collecting
the result. Finally
it requires that there is nothing left in *unparsed*
and returns the result of parse-sentence.
Readers who appreciate the dangers of global state and mutation
might be wondering what on earth is going on here. A function that
accepts an argument then just assigns it to a global variable?
Worse, it then proceeds to mutate that global as the parse proceeds?
Surely that is the antithesis of good programming? There is a very
sound reason that it is done this way, and that is to demonstrate
what amb is capable of. Please bear with me.
parse will be called like (parse '(fruit flies
like a bannanna)) and should return a parse tree with the
nodes of the tree labelled, like:
(sentence (noun-phrase (adj fruit)
(noun flies))
(verb-phrase (verb like)
(noun-phrase (det a)
(noun bannanna))))
We have seen that parse calls parse-sentence,
and we shall see shortly that parse-sentence calls out
to other parse-noun-phrase etc. routines to futher
break down the sentence. The various parse-* routines
all indirectly consume tokens from the global *unparsed*
variable, but the only function that directly removes tokens from
*unparsed* is the function parse-word:
(define parse-word
(lambda (words)
(begin
(require *unparsed*)
(require (member? (car *unparsed*) (cdr words)))
(let ((found-word (car *unparsed*)))
(begin
(set! *unparsed* (cdr *unparsed*))
(list (car words) found-word))))))
The argument words will be one of the lists of words
defined above, where the car is the type of the words and the cdr
is the actual words to be recognized. Hence the use of car
and cdr to get the appropriate components.
So parse-word is called like (parse-word
nouns) and will succeed and return a list of a type and a
word if the first word of *unparsed* is one of its
argument words. For example if *unparsed* is '(flies
like an arrow) and we call (parse-word nouns) it
should return the list (noun flies) and as a side effect
set *unparsed* to '(like an arrow).
parse-word requires that there are tokens left to
parse, then requires that the first word of *unparsed*
is a member of its list of candidate words. If so then it removes
the first word from *unparsed* and returns it, appended
to the category of words that matched. If there are no words left
to parse, or if the next word in *unparsed* is not one
of the argument words, then parse-word fails
and control backtracks to the previous decision point where the
next alternative is tried. It is important to remember here that
the effect of set! on *unparsed* can be undone by the
backtracking of amb.
Back to parse. parse calls
parse-sentence:
(define parse-sentence
(lambda ()
(amb (list 'sentence
(parse-word nouns)
(parse-verb-phrase))
(list 'sentence
(parse-noun-phrase)
(parse-verb-phrase)))))
parse-sentence ambivalently chooses to parse either
the structure of the first sentence or the structure of the second.
It prepends the result with the appropriate grammatical label just
as parse-word did.
Since the second part of both sentences is the same (a verb
phrase) we could equivalently have said:
(define parse-sentence
(lambda ()
(list 'sentence
(amb (parse-word nouns)
(parse-noun-phrase))
(parse-verb-phrase))))
In fact this second formulation is likely to be more efficient
since it doesn't have to backtrack through parse-verb-phrase
unneccessarily.
Next let's look at parse-verb-phrase. Our two example
verb phrases are different. The first consists of a verb and a
prepositional phrase, the second consists of a verb and a noun
phrase. We can combine the two, eliminating the duplication on verbs
for a slightly more efficient parse. Here's
parse-verb-phrase:
(define parse-verb-phrase
(lambda ()
(list 'verb-phrase
(parse-word verbs)
(amb (parse-prep-phrase)
(parse-noun-phrase)))))
Going bredth-first from parse-sentence, next up is
parse-noun-phrase:
(define parse-noun-phrase
(lambda ()
(list 'noun-phrase
(amb (parse-word adjectives)
(parse-word determinants))
(parse-word nouns))))
We have two example noun phrases: an adjective followed by a
noun and a determinant followed by a noun. Again we've removed the
duplication, this time on the noun.
Lastly, we have to parse prepositional phrases, of which we have
only one example: a preposition followed by a noun phrase:
(define parse-prep-phrase
(lambda ()
(list 'prep-phrase
(parse-word prepositions)
(parse-noun-phrase))))
With these definitions in place, we can attempt to parse our two
sentences (output reformatted manually to aid readability):
> (parse '(time flies like an arrow))
(sentence (noun time)
(verb-phrase (verb flies)
(prep-phrase (prep like)
(noun-phrase (det an)
(noun arrow)))))
> ?
(sentence (noun-phrase (adj time)
(noun flies))
(verb-phrase (verb like)
(noun-phrase (det an)
(noun arrow))))
> ?
Error: no more solutions
and
>(parse '(fruit flies like a bannanna))
(sentence (noun fruit)
(verb-phrase (verb flies)
(prep-phrase (prep like)
(noun-phrase (det a)
(noun bannanna)))))
> ?
(sentence (noun-phrase (adj fruit)
(noun flies))
(verb-phrase (verb like)
(noun-phrase (det a)
(noun bannanna))))
> ?
Error: no more solutions
So while time does indeed fly like an arrow, and fruit flies are
fond of bannannas, other valid parses of the sentences
imply that some strange creatures called “time flies” are
attracted to arrows, and that fruit does fly much like a
bannanna does.
What makes this really exciting is that we are still in backtracking
mode when the parse is complete. If we don't like a particular
result we can request further results by hitting “?”
at the prompt, but this option is also available to client code
of the parser: Subsequent downstream analysis of the result
may reject it on semantic grounds (fruit can't fly, no such thing
as “time flies”), and request an alternative parse.
So you've seen what amb can do. The rest of this chapter
discusses its implementation.
16.3. Implementing amb
The core idea behind amb is to use an additional continuation
to let us do
backtracking. Instead of just passing around one
continuation that specifies the point of return for the called
function, we pass around two continuations. The first continuation
is the same as before, and that takes care of normal control flow.
The second continuation is a “failure” continuation of no arguments that
gets called by amb when it runs out of options, and by
the repl when you type in a “?”. That failure
continuation resumes execution at the previous decision point.
Here's a useful analogy to help keep track of what is going on.
If you
consider normal control flow, both calls to methods and
calls (returns) to normal continuations to be always “downstream”
towards the successful production of a result, then the invocation
of the failure continuation causes control to pass back “upstream”
to a previous point in the computation and resume from there.
The initial failure continuation is passed to Read()
by the repl to produce
the “no current problem” error and restart the repl (in
fact Error() already restarts the repl for us). Then when
the repl invokes Eval() on an expression it has read,
it passes an alternative “no more
solutions” failure continuation which again calls
Error(). These initial failure continuations
are as far “upstream” as you can get because they exist before
the computation is even attempted.
Now if amb is invoked,
it replaces the current
failure continuation with a new one that, if called, will cause
amb either to pass its next value back “downstream” again
(to the success continuation) or, if there are no more choices, to
retreat even further “upstream” to the previous failure
continuation. That's all we have to achieve really, the rest of this
chapter is just the details.
There are however another couple of places
where the failure continuation needs to be treated specially.
Remember my little rant about purely functional languages
at the start of Section 10.1?
Well in a purely functional language there would be no such
extra places, because it is only side effects that need to be
undone as the failure continuation backtracks upstream through them.
Both define and set! need to install their
own failure continuations that will undo whatever change they
made, then call the previous failure continuation to continue
back upstream.
As you might have guessed, amb requires another rewrite
of our interpreter. However this time the rewrite is, on the whole, a purely
mechanical one. Apart from the places mentioned above, the failure
continuation is always simply passed through untouched. It is an extra
argument to all the methods that take a continuation argument,
and the success continuations themselves now
all take an extra failure continuation as argument too, since
the failure continuation must not be lost track of.
16.3.1. Changes to Continuations
Notice that we now have three
kinds of continuation: a success continuation for normal control
flow, a failure continuation for backtracking, and let's not forget
the continuation of no arguments returned to the trampoline to clear
the stack. It was becoming obvious that if I just stuck with cont{}
to create all continuations, I would have to start to
litter the code with comments to the effect of “this is the
success continuation”, “this is the failure continuation”
etc. It makes much more sense to make the
original PScm::Continuation class abstract, and to have
concrete subclasses for each of these types. Then, instead of
the generic cont{} construct to create a continuation,
we now have three separate prototyped subroutines
to create continuations of the appropriate type. The cont{}
construct still creates the “normal” continuations, but new constructs
fail{} and bounce{} create the other types of continuation.
So without further ado, here's the new abstract
PScm::Continuation class:
1 package PScm::Continuation;
2
3 use strict;
4 use warnings;
5 use base qw(PScm::Expr);
6
7 require Exporter;
8
9 push our @ISA, qw(Exporter);
10
11 our @EXPORT = qw(bounce cont fail);
12
13 sub new {
14 my ($class, $cont) = @_;
15 bless { cont => $cont }, $class;
16 }
17
18 sub cont(&) {
19 my ($cont) = @_;
20 return PScm::Continuation::Cont->new($cont);
21 }
22
23 sub fail(&) {
24 my ($fail) = @_;
25 return PScm::Continuation::Fail->new($fail);
26 }
27
28 sub bounce(&) {
29 my ($bounce) = @_;
30 return PScm::Continuation::Bounce->new($bounce);
31 }
The cont sub now creates a PScm::Continuation::Cont
object instead of a PScm::Continuation object.
The new
fail and bounce subs are completely analogous.
Additionally, instead of the three new continuation classes sharing
a common Cont() method to invoke the continuation,
Cont() has been moved to the
PScm::Continuation::Cont class,
and the PScm::Continuation::Fail class has a
Fail() method. These are both almost identical to the earlier
generic Cont() method, but expect the correct number of
arguments etc. The old Bounce() method, which invoked the
continuation directly, has just been moved into the
PScm::Continuation::Bounce class.
16.3.2. Mechanical Transformations of the Interpreter
I don't want to show you those other PScm::Continuation
derived classes yet, because that would jump the gun on the passing
of the new failure continuation around in Apply() etc. Instead,
now we know what fail{} and bounce{}
do, lets take a look at some examples of how this mechanical
rewrite of the interpreter will proceed.
The default Eval() method in PScm::Expr
demonstrates the
simplest kind of transformation. The previous version simply
called its continuation on $self, so by default
expressions evaluate to themselves.
The new amb version takes an extra $fail continuation as argument,
and passes it along to the original continuation as an extra argument:
16 sub Eval {
17 my ($self, $env, $cont, $fail) = @_;
18 $cont->Cont($self, $fail);
19 }
Next up, let's take a look at transforming an example method
that creates a new continuation. The PScm::SpecialForm::Let::Apply()
method does that. It extends the current environment with the new
bindings for the let expression, passing a continuation that
will evaluate the body of the let in that new environment. The
new version for amb is not that different. As you can see all
the method calls that used to take a single continuation as argument
now take an extra $fail continuation, and the original
continuations themselves now take an extra $fail continuation,
passing it to any method that now expects it. Otherwise, it's
unchanged:
13 sub Apply {
14 my ($self, $form, $env, $cont, $fail) = @_;
15
16 my ($symbols, $values, $body) = $self->UnPack($form);
17
18 $env->Extend(
19 $symbols, $values,
20 cont {
21 my ($newenv, $fail) = @_;
22 $body->Eval($newenv, $cont, $fail);
23 },
24 $fail
25 );
26 }
Please note however that there are two $fail variables here.
The first one is passed to Apply() as argument on
Line 14
and gets passed on
as an additional argument to Extend() on
Line 24.
The second $fail
is argument to the new continuation on
Line 21
and is passed on as an additional
argument to Eval() on
Line 22.
It is very important that these two $fail variables
are kept distinct.
Before we finally get around to some code that actually does more
than just pass the failure continuation around, let's take a look
at a fairly involved use of continuations, and the (still mechanical)
transformation that amb requires of it.
In Section 8.5.1 we introduced
PScm::Expr::List::Pair::map_eval(), which
evaluates each component of its list and returns an arrayref of
those evaluated components. That method
was introduced even earlier in our CPS rewrite in
Section 13.6.2
and was finally reunited with its original list implementation
in
Section 13.6.5
where it deals with both continuations and true PScheme lists.
Here's PScm::Expr::List::Pair::map_eval() so far:
157 sub map_eval {
158 my ($self, $env, $cont) = @_;
159
160 $self->[FIRST]->Eval(
161 $env,
162 cont {
163 my ($evaluated_first) = @_;
164 $self->[REST]->map_eval(
165 $env,
166 cont {
167 my ($evaluated_rest) = @_;
168 $cont->Cont($self->Cons($evaluated_first,
169 $evaluated_rest));
170 }
171 );
172 }
173 );
174 }
And here it is after the amb changes:
171 sub map_eval {
172 my ($self, $env, $cont, $fail) = @_;
173
174 $self->[FIRST]->Eval(
175 $env,
176 cont {
177 my ($evaluated_first, $fail) = @_;
178 $self->[REST]->map_eval(
179 $env,
180 cont {
181 my ($evaluated_rest, $fail) = @_;
182 $cont->Cont(
183 $self->Cons($evaluated_first,
184 $evaluated_rest),
185 $fail
186 );
187 },
188 $fail
189 );
190 },
191 $fail
192 );
193 }
It's a bit longer, but I hope you can see that the only change
is that extra $fail argument alongside each passed
continuation, and as an extra argument to any continuation which
is actually called. Note again that it's very important that each
continuation actually declares its extra argument. Although the
same $fail variable name is used throughout, the actual
scope of each variable is different, and could easily have a different
value. Having said that, this is the main reason that this rewrite
is so mechanical.
16.3.3. Remaining Continuation Changes
Now that we've seen examples of how the failure continuation
gets passed around, it's safe to return to our
PScm::Continuation classes and show the details of the
various methods therein. Firstly, here's the
PScm::Continuation::Cont class.
34 package PScm::Continuation::Cont;
35
36 use strict;
37 use warnings;
38 use base qw(PScm::Continuation);
39
40 BEGIN {
41 *cont = \&PScm::Continuation::cont;
42 *bounce = \&PScm::Continuation::bounce;
43 }
44
45 sub Apply {
46 my ($self, $form, $env, $cont, $fail) = @_;
47 $form->map_eval(
48 $env,
49 cont {
50 my ($evaluated_args, $fail) = @_;
51 $self->Cont($evaluated_args->first, $fail);
52 },
53 $fail
54 );
55 }
56
57 sub Cont {
58 my ($self, $arg, $fail) = @_;
59
60 bounce { $self->{cont}->($arg, $fail) }
61 }
We have to manually import the cont and bounce
subroutines from PScm::Continuation
because they're in the same file (a failure of use base.) Then on
Lines 45–55
we see the
Apply() method for continuations (remember call/cc presents
continuations as functions so they need an Apply() method.)
Apply() is unchanged
except for the passing of the extra $fail continuation. This
means that the failure continuation is kept track of even through
the use of call/cc.
Lastly the Cont() method is similarily unchanged except that it
uses bounce{} instead of cont{} to create a
PScm::Continuation::Bounce
for the trampoline, and of course it has the extra $fail
continuation to pass on.
PScm::Continuation::Fail is somewhat shorter:
64 package PScm::Continuation::Fail;
65
66 use strict;
67 use warnings;
68 use base qw(PScm::Continuation);
69
70 BEGIN { *bounce = \&PScm::Continuation::bounce; }
71
72 sub Fail {
73 my ($self) = @_;
74 bounce { $self->{cont}->() }
75 }
Again we must manually import the bounce{} construct
that we need, but then the Fail(), method, which takes
no arguments, merely returns a bounce{} continuation
to the trampoline that will invoke the failure continuation
with no arguments.
PScm::Continuation::Bounce is even shorter. It's
single Bounce() method, again with no arguments,
directly invokes its stored continuation as it always did.
78 package PScm::Continuation::Bounce;
79
80 use strict;
81 use warnings;
82 use base qw(PScm::Continuation);
83
84 sub Bounce {
85 my ($self) = @_;
86 $self->{cont}->();
87 }
88
89 1;
So back to the rewrite. How about actually doing something with
the failure continuation? As I've said, there are only a few places
in the interpreter where a new failure continuation is constructed,
namely
- in the
Apply() method for amb iteslf;
- in the
Apply() method for define;
- in the
Apply() method for set!;
- in the repl.
These are the only places in the interpreter where the amb rewrite
is not purely mechanical.
We'll go through these cases in the same order, starting with
PScm::SpecialForm::Amb::Apply().
16.3.4. amb Itself
amb is the whole point of this chapter,
and so deserves some attention. This special form must
evaluate and return its first argument “downstream” when it
is called, but if control backtracks to it then it must return its next
argument, and so on, until the argument list is exhausted at which
point it should invoke the failure continuation that it was originally
called with and backtrack further upstream:
477 package PScm::SpecialForm::Amb;
478
479 use base qw(PScm::SpecialForm);
480
481 use PScm::Continuation;
482
483 sub Apply {
484 my ($self, $choices, $env, $cont, $fail) = @_;
485 if ($choices->is_pair) {
486 $choices->first->Eval(
487 $env,
488 $cont,
489 fail {
490 $self->Apply(
491 $choices->rest,
492 $env,
493 $cont,
494 $fail
495 )
496 }
497 )
498 } else {
499 $fail->Fail();
500 }
501 }
502
503 1;
It's really not that bad. It takes the same arguments as any
normal Apply() method, including the extra failure continuation.
On Line 485 it tests to see
if the argument $choices (the actual arguments to the
amb function) is the empty list. If $choices is not
empty, then on Line 486 it
evaluates the first choice, passing the original success continuation
$cont which will return the result downstream to the caller.
But instead of just passing in its argument $fail
continuation, on Lines 489–496
it passes a new fail{} continuation that will, if backtracked to,
call Amb::Apply()
again on the rest of the arguments. Note that on Line 494 the new failure continuation
passes amb's original failure continuation to Amb::Apply(). So if amb
itself decides to backtrack by calling that, control will pass
immediately back to whatever failure continuation was in place
before amb installed this new one. If on the other hand the new
failure continuation is ever invoked downstream of this, it will
cause control to proceed back upstream to this occurence of amb
which then returns its next value back downstream via Apply() to
the current success continuation.
If the list of arguments is empty, then on
Line 499
Apply() invokes
its original argument $fail continuation causing execution to
immediately backtrack further upstream.
16.3.5. Changes to define
Next, let's take a look at define. define installs its
symbol/value pair in the current environment frame, reguardless of
the presence or absence of any previous binding. The amb
version of define must undo whatever it did if it is backtracked
through, so it needs to remember the previous value, if any. Here's the
amb version of PScm::SpecialForm::Define::Apply():
331 sub Apply {
332 my ($self, $form, $env, $cont, $fail) = @_;
333 my ($symbol, $expr) = $form->value;
334 my $old_value = $env->LookUpHere($symbol);
335
336 $expr->Eval(
337 $env,
338 cont {
339 my ($value, $fail) = @_;
340 $cont->Cont(
341 $env->Define($symbol, $value),
342 fail {
343 if (defined $old_value) {
344 $env->Assign($symbol, $old_value);
345 } else {
346 $env->UnSet($symbol);
347 }
348 $fail->Fail();
349 }
350 );
351 },
352 $fail
353 );
354 }
define in the previous version evaluated its value part in
the current environment, passing a continuation that would call the
top environment frame's Define() method on the symbol and the result.
This new version must additionally keep track of the previous value
of the symbol, if any, and arrange that its failure continuation
restores that value before backtracking further. Apart from the
extra $fail argument, the first thing that is new is that
on Line 334 it calls a
new method PScm::Env::LookUpHere() which only looks in
the top frame and returns either
the value of the argument symbol or undef. Then things
proceed as normal apart from the extra $fail continuation
until Lines 342–349 where a
replacement fail{} continuation is passed to define's original
success continuation.
That new fail{} continuation checks to see if the $old_value
is defined. If it is, then it calls Assign() on the
environment to restore the old value. If it is not defined (there was
no previous value) then it must call a new method of
PScm::Env, UnSet(), to remove the binding from
the top frame. In either case, it finally returns through the
original $fail continuation to backtrack further upstream.
The location of the fail{} is quite subtle, in fact an
earlier version of this code had a bug that went unnoticed for a
considerable time. Consider the following PScheme fragment (assume
x is already defined):
(define x (cons (amb 1 2) x))
Obviously, when backtracking, we want the previous value of
x to be restored before we cons the next value from amb
on to it, otherwise we would be breaking the semantics of chronological
backtracking. i.e. if x starts out as (5), then
after the first time throught it will obviously be (1 5),
and the second time through it should be (2 5).
Now, referring to Figure 16.4,
think about the order that things happen here. Passing continuations
is much like tearing a function into two or more pieces: the first
piece is the “head” of the function, before it makes any calls of its own.
The remaining pieces are
the continuations that it passes to the functions that it calls.
This figure omits many details, but you can see
that define calls cons which calls amb, then amb calls the
continuation of cons which in turn calls the waiting continuation
of define. By the way this is another example of CPS being a
simplification in that it linearizes control flow.
In this figure, “downstream” is left to right and
“upstream” is right to left. Additionally the circles represent
new failure continuations being created and passed downstream. If
control backtracks upstream into this piece of code, it will first
encounter the most recently installed, e.g. the rightmost
failure continuation. You can see that amb installs a new failure
continuation at 1, and that in order for define to have its failure
continuation supplant the one set up by amb it must
be created downstream of amb's. Therefore it is
define's success continuation that must install the failure
continuation, at 2 in the figure.
If instead the initial code on entry to define had installed
the failure continuation at 0 (by passing it as the last argument
to the outermost Eval), then backtracking would find amb's
failure continuation first, and define would not get a chance to
undo its effect before amb sent its next value downstream again.
That was the bug of course, setting up the failure continuation at 0 instead
of 2—it works almost all of the
time, unless evaluation of the second argument to define or set!
results in a call to amb.
16.3.6. Changes to set!
Next we're going to look at set!.
set! searches the environment for a binding and
replaces it, throwing an error if no binding can be found. First
of all, here's the new definition for
PScm::SpecialForm::Set::Apply():
208 sub Apply {
209 my ($self, $form, $env, $cont, $fail) = @_;
210 my ($symbol, $expr) = $form->value;
211 my $old_value = $env->LookUpNoError($symbol);
212 $expr->Eval(
213 $env,
214 cont {
215 my ($val, $fail) = @_;
216 my $result = eval { $env->Assign($symbol, $val) };
217 if ($@) {
218 $self->Error($@, $env);
219 } else {
220 $cont->Cont(
221 $result,
222 fail {
223 $env->Assign($symbol, $old_value);
224 $fail->Fail();
225 }
226 );
227 }
228 },
229 $fail
230 );
231 }
This is similar to PScm::SpecialForm::Define::Apply()
above, but it uses another new method of PScm::Env,
LookUpNoError() to see if the variable being set had
a previous value in any frame. Then it proceeds as it did,
Passing a continuation to the Eval() of the expression
that will call Assign() on the environment,
trapping any error.
But then it installs a new
failure continuation that will, if invoked, restore the previous value and
backtrack further. This new failure continuation just assigns the
previous value and backtracks. It need
not worry that there was no previous value, since in that case
the code in the success continuation would have invoked Error(),
thus restarting the repl,
and the failure continuation would never be backtracked through.
The same subtleties described in define apply here: set! must
pass its new failure continuation to the original success continuation
passed to set!, rather than to the eval of the value to be assigned,
in case that evaluation contains an amb. The set! failure continuation
that undoes the mutation must be backtracked
through before any amb failure continuation.
16.3.7. Changes to repl()
It is not without reason that I've kept the changes to the repl
until last. This is the most complex part of the amb rewrite.
If you remember from Section 13.6.2 ReadEvalPrint()
now calls a helper routine repl() to do the heavy lifting,
and it is repl() that we see here undergoing significant
change.
However there is nothing here that is really new, now that you've
seen the mechanics of the rest of the rewrite. It is mostly complicated
because the original repl() method was already complicated.
Here's repl() from the previous version of the interpreter:
79 sub repl {
80 my ($env, $reader, $outfh) = @_;
81 $reader->Read(
82 cont {
83 my ($expr) = @_;
84 $expr->Eval(
85 $env,
86 cont {
87 my ($result) = @_;
88 $result->Print(
89 $outfh,
90 cont {
91 repl($env, $reader, $outfh);
92 }
93 )
94 }
95 )
96 }
97 )
98 }
As I've said before, it's really just Read() called
with a continuation that calls Eval() with a continuation
that calls Print() with a continuation that calls repl()
again. As before there are going to be extra failure continuations
passed around, but that part of the rewrite is purely mechanical.
The additional complications are because repl() must additionally
install the final upstream failure continuations, and additionally
must check if the expression just read is a “?”
request to backtrack. Bearing all that in mind it's really not
too bad:
87 sub repl {
88 my ($env, $reader, $outfh, $fail1) = @_;
89 $fail1 ||= fail { __PACKAGE__->Error("no current problem", $env) };
90 $reader->Read(
91 cont {
92 my ($expr, $fail2) = @_;
93 $expr->Eval(
94 $env,
95 cont {
96 my ($result, $fail3) = @_;
97 $result->Print(
98 $outfh,
99 cont {
100 my ($dummy, $fail4) = @_;
101 repl($env, $reader, $outfh, $fail4);
102 },
103 $fail3
104 )
105 },
106 fail {
107 __PACKAGE__->Error("no more solutions", $env);
108 }
109 )
110 },
111 $fail1
112 )
113 }
To aid readability somewhat, I've named the various occurences
of the failure coninuation separately: $fail1, $fail2
etc. They could all just be called $fail without breaking
anything, but it would be more confusing.
The $fail1 argument to repl() is optional. Neither
Error() nor the new_thread() call that initially installs
the repl on the trampoline bother to pass one. If no failure continuation
is passed, then on
Line 89
repl() defaults it to a call to Error() with a
“no current problem” message.
Then, as before repl()
calls Read() with a continuation that will call Eval() etc.
Read() itself changes slightly however: if it reads a
“?” it will invoke the current failure continuation.
If the expression
read is not a retry request, then everything proceeds as normal,
bar the extra failure continuations: Eval() is called with a
continuation that calls Print() with a continuation that
calls repl() again. Note that on Line 101 the continuation passed to Print() calls
repl() with its argument failure continuation
$fail4, which
is how backtracking works when a “?” is read
subsequently.
One last thing to notice. On
Lines 106–108
The failure continuation passed to Eval() produces the
“no more solutions” error, which will be printed
if required before repl() reinstates the default
“no current problem” failure.
As mentioned above, Read() has changed a little.
Here's the new definition:
94 sub Read {
95 my ($self, $cont, $fail) = @_;
96 my $res = $self->_read();
97 return undef unless defined $res;
98 if ($res->is_retry) {
99 $fail->Fail();
100 } else {
101 $cont->Cont($res, $fail);
102 }
103 }
Before returning its value, Read() must first check that the
expression it is about to pass to its success continuation is not
“?”.
On Line 98 Read()
checks to see if the expression returned by _read() is a
retry request. is_retry() is defined to return false in
PScm::Expr, but PScm::Expr::Symbol redefines
this to return true if the symbol's value() is “?”.
If it is a retry request, Read() invokes its argument
failure continuation. At the very start this will be the "no
current problem" error, so typing “?” at a
fresh PScheme prompt will produce this error.
That's really all there is to amb. The rest of this section
joins the dots by showing the support routines that I've glossed over.
16.3.8. Additional Changes
There's not really
many of those to describe. If you remember there were a couple of
extra methods added to PScm::Env to aid define and
set! in undoing their changes. The first of these was
LookUpHere():
159 sub LookUpHere {
160 my ($self, $symbol) = @_;
161 if (exists($self->{bindings}{ $symbol->value })) {
162 return $self->{bindings}{ $symbol->value };
163 } else {
164 return undef;
165 }
166 }
LookUpHere() just checks the current frame to see if the
binding exists. It is called by our new define to save any
previous value before define replaces it.
Next is LookUpNoError():
149 sub LookUpNoError {
150 my ($self, $symbol) = @_;
151
152 if (defined(my $ref = $self->_lookup_ref($symbol))) {
153 return $$ref;
154 } else {
155 return undef;
156 }
157 }
It uses the existing _lookup_ref() method to locate the
symbol, either dereferencing and returning the value if it was found,
or returning undef.
LookUpNoError() is called by set! before assigning a new
value to the found variable.
The other addition to PScm::Env was an UnSet()
method which would remove a binding from the environment.
191 sub UnSet {
192 my ($self, $symbol) = @_;
193 delete $self->{bindings}{ $symbol->value };
194 }
This method just deletes a binding from the current frame.
It is only called by define
when backtracking to remove the setting that define added
to the current environment frame, so it need not, and should not recurse.
Finally, and most trivially, there is an is_retry() method
of PScm::Expr, so that the continuation passed to
Read() can ask politely if the expression just read is a
request to backtrack (“?”).
The base PScm::Expr class
defines this to be false as a default:
14 sub is_retry { 0 }
But PScm::Expr::Symbol redefines this to return true if
the symbol's value() is "?".
281 sub is_retry {
282 my ($self) = @_;
283 return $self->value eq "?";
284 }
16.4. Support for Testing amb
The examples at the start of this chapter in
Section 16.1
made use of quite a few support functions of various sorts.
Most of those functions could be defined directly in the
PScheme language, but a few remaining functions were left to be
implemented in the interpreter itself. Specifically, those
functions were:
- and and or. Both are special forms so that
arguments do not get evaluated unnecessarily and short-circuit
evaluation is possible.
- Numeric inequality tests >, <,
>= and <=.
- A general equality test eq?. This function will work
for numbers, symbols, strings and lists (two lists are considered
eq? if their cars are eq? and their
cdrs are eq?).
16.4.1. and and or
It is best to make these both special forms, so that
they do not evaluate their arguments unnecessarily. In fact they
share quite a bit in common with the existing begin
special form. begin evaluates all its arguments in turn,
wheras and and or evaluate each of their arguments
until some condition is met. If you remember from
Section 13.6.7,
PScm::SpecialForm::Begin::Apply() called out to a helper function
apply_next() if its argument list was non-empty. What I've done
is to create a common abstract base class
PScm::SpecialForm::Sequence for all of begin,
and and or, because they can all share a common
Apply() method:
234 package PScm::SpecialForm::Sequence;
235
236 use base qw(PScm::SpecialForm);
237
238 sub Apply {
239 my ($self, $form, $env, $cont, $fail) = @_;
240 if ($form->is_pair) {
241 $self->apply_next($form, $env, $cont, $fail);
242 } else {
243 $cont->Cont($form, $fail);
244 }
245 }
PScm::SpecialForm::Begin inherits from that to get
its Apply() method, its apply_next() is unchanged other than having
the extra failure continuation:
249 package PScm::SpecialForm::Begin;
250
251 use base qw(PScm::SpecialForm::Sequence);
252 use PScm::Continuation;
253
254 sub apply_next {
255 my ($self, $form, $env, $cont, $fail) = @_;
256
257 $form->first->Eval(
258 $env,
259 cont {
260 my ($val, $fail) = @_;
261 if ($form->rest->is_pair) {
262 $self->apply_next($form->rest, $env, $cont, $fail);
263 } else {
264 $cont->Cont($val, $fail);
265 }
266 },
267 $fail
268 );
269 }
PScm::SpecialForm::And reimplements apply_next()
to return false as soon as an evaluated value is false. If all of the arguments
to and are true, and returns the value of the
last argument.
272 package PScm::SpecialForm::And;
273
274 use base qw(PScm::SpecialForm::Sequence);
275 use PScm::Continuation;
276
277 sub apply_next {
278 my ($self, $form, $env, $cont, $fail) = @_;
279
280 $form->first->Eval(
281 $env,
282 cont {
283 my ($val, $fail) = @_;
284 if ($form->rest->is_pair) {
285 if ($val->isTrue) {
286 $self->apply_next($form->rest, $env, $cont, $fail);
287 } else {
288 $cont->Cont($val, $fail);
289 }
290 } else {
291 $cont->Cont($val, $fail);
292 }
293 },
294 $fail
295 );
296 }
PScm::SpecialForm::Or behaves similarily. it evaluates
each of its arguments until one of them is true, in which case it returns that
result. If all of its arguments are false, it returns false.
299 package PScm::SpecialForm::Or;
300
301 use base qw(PScm::SpecialForm::Sequence);
302 use PScm::Continuation;
303
304 sub apply_next {
305 my ($self, $form, $env, $cont, $fail) = @_;
306
307 $form->first->Eval(
308 $env,
309 cont {
310 my ($val, $fail) = @_;
311 if ($form->rest->is_pair) {
312 if ($val->isTrue) {
313 $cont->Cont($val, $fail);
314 } else {
315 $self->apply_next($form->rest, $env, $cont, $fail);
316 }
317 } else {
318 $cont->Cont($val, $fail);
319 }
320 },
321 $fail
322 );
323 }
16.4.2. Numeric Inequality Tests
The next thing we'll need is a numeric inequality test
“>”.
The full standard set of numeric inequality tests
“<”,
“>”,
“<=”, and
“>=” now exist as primitives in the interpreter.
They are all
under PScm::Primitive, in fact they all descend from
a subclass of that called PScm::Primitive::Compare
which provides a common _apply() method:
159 package PScm::Primitive::Compare;
160
161 use base qw(PScm::Primitive);
162
163 sub _apply {
164 my ($self, @numbers) = @_;
165 $self->_check_type($numbers[0], 'PScm::Expr::Number') if @numbers;
166 while (@numbers > 1) {
167 my $number = shift @numbers;
168 $self->_check_type($numbers[0], 'PScm::Expr::Number');
169 return PScm::Expr::Number->new(0)
170 unless $self->_compare($number, $numbers[0]);
171 }
172 return PScm::Expr::Number->new(1);
173 }
So they all take an arbitrary number of arguments like the
arithmetic primitives. For example (<= 2 3 3 4) is true
because each argument is “<=” the next argument.
_apply() iterates over its arguments, checking each one is a number
and calling a separate _compare() method on each pair.
The _compare() method called on
Line 170
is implemented separately by each of
PScm::Primitive::Lt,
PScm::Primitive::Gt,
PScm::Primitive::Le and
PScm::Primitive::Ge. They all go exactly the same way,
so for example here's PScm::Primitive::Lt:
176 package PScm::Primitive::Lt;
177
178 use base qw(PScm::Primitive::Compare);
179
180 sub _compare {
181 my ($self, $first, $second) = @_;
182 return $first->value < $second->value;
183 }
Only the actual comparison operator differs between the implementations.
16.4.3. eq?
Finally eq?. The
eq? implementation is a bit more interesting. It can be used to compare
any PScheme data types that inherit from PScm::Expr.
Equality is a relative term however. For instance,
unlike Perl, a string and a number will never be considered equal, however
two lists with the same content are considered equal.
Here's the new
PScm::Primitive::Eq class:
145 package PScm::Primitive::Eq;
146
147 use base qw(PScm::Primitive);
148
149 sub _apply {
150 my ($self, @things) = @_;
151 while (@things > 1) {
152 my $thing = shift @things;
153 return PScm::Expr::Number->new(0) unless $thing->Eq($things[0]);
154 }
155 return PScm::Expr::Number->new(1);
156 }
As you can see, like the inequality tests above,
it will take an arbitrary number of arguments.
Apply() keeps comparing adjacent arguments
by calling their Eq() method until a test fails, or all
tests pass. The Eq() method is defined differently for
various types of PScm::Expr. A default method in the
base PScm::Expr just compares object identity:
40 sub Eq {
41 my ($self, $other) = @_;
42 return $self == $other;
43 }
This means that, for example, two functions with the same
arguments, env and body would still not be considered equal.
This could be fixed, but I'm not sure it's worth it.
Anyway PScm::Expr::Atom overrides this Eq()
method to do a string
comparison on the (scalar) values of the two objects, first
checking that the two objects are of the same type. This
is good enough for strings, numbers and symbols:
92 sub Eq {
93 my ($self, $other) = @_;
94 return 0 unless $other->isa(ref($self));
95 return $self->value eq $other->value;
96 }
PScm::Expr::List::Pair::Eq() is more interesting. Firstly
it does a quick check for object identity, that will save
unnecessary recursion if the two objects are actually the
same object. Then it checks that the object is a list, and finally
it recursively calls itself on both first() and rest()
to complete the test:
228 sub Eq {
229 my ($self, $other) = @_;
230 return 1 if $self == $other;
231 return 0 unless $other->is_pair;
232 return $self->[FIRST]->Eq($other->[FIRST]) &&
233 $self->[REST]->Eq($other->[REST]);
234 }
Last of the Eq() methods is in PScm::Expr::List::Null.
This method returns true only if the other object is also a
PScm::Expr::List::Null, since null is only equal to null:
255 sub Eq {
256 my ($self, $other) = @_;
257 return $other->is_null;
258 }
16.4.4. Wiring it up
Finally, here's the additional methods wired in to ReadEvalPrint().
You can also see that on
Line 67
the new_thread() routine installs a bounce{} continuation
that starts the repl. That continuation doesn't pass a failure continuation
to repl(), so repl() will default that to the
Error: no current problem error.
35 sub ReadEvalPrint {
36 my ($infh, $outfh) = @_;
37
38 $outfh ||= new FileHandle(">-");
39 my $reader = new PScm::Read($infh);
40 my $initial_env;
41 $initial_env = new PScm::Env(
42 let => new PScm::SpecialForm::Let(),
43 '*' => new PScm::Primitive::Multiply(),
44 '-' => new PScm::Primitive::Subtract(),
45 '+' => new PScm::Primitive::Add(),
46 if => new PScm::SpecialForm::If(),
47 lambda => new PScm::SpecialForm::Lambda(),
48 list => new PScm::Primitive::List(),
49 car => new PScm::Primitive::Car(),
50 cdr => new PScm::Primitive::Cdr(),
51 cons => new PScm::Primitive::Cons(),
52 letrec => new PScm::SpecialForm::LetRec(),
53 'let*' => new PScm::SpecialForm::LetStar(),
54 eval => new PScm::SpecialForm::Eval(),
55 macro => new PScm::SpecialForm::Macro(),
56 quote => new PScm::SpecialForm::Quote(),
57 'set!' => new PScm::SpecialForm::Set(),
58 begin => new PScm::SpecialForm::Begin(),
59 define => new PScm::SpecialForm::Define(),
60 'make-class' => new PScm::SpecialForm::MakeClass(),
61 'call/cc' => new PScm::SpecialForm::CallCC(),
62 print => new PScm::SpecialForm::Print($outfh),
63 spawn => new PScm::SpecialForm::Spawn(),
64 exit => new PScm::SpecialForm::Exit(),
65 error => new PScm::SpecialForm::Error(
66 $outfh,
67 bounce { repl($initial_env, $reader, $outfh) }
68 ),
69 amb => new PScm::SpecialForm::Amb(),
70 'eq?' => new PScm::Primitive::Eq(),
71 '>' => new PScm::Primitive::Gt(),
72 '<' => new PScm::Primitive::Lt(),
73 '>=' => new PScm::Primitive::Ge(),
74 '<=' => new PScm::Primitive::Le(),
75 and => new PScm::SpecialForm::And(),
76 or => new PScm::SpecialForm::Or(),
77 );
78
79 $initial_env->Define(
80 PScm::Expr::Symbol->new("root"),
81 PScm::Class::Root->new($initial_env)
82 );
83 __PACKAGE__->new_thread(bounce { repl($initial_env, $reader, $outfh) });
84 trampoline();
85 }
16.6. Tests
The first set of tests in Listing 30 tries
out or equality and inequality operators. It's nice to know they
all work as expected.
Listing 30. t/PScm_Compare.t 1 use strict;
2 use warnings;
3 use Test::More;
4 use lib './t/lib';
5 use PScm::Test tests => 38;
6
7 BEGIN { use_ok('PScm') }
8
9 eval_ok('(eq? 1 1)', '1', 'eq numbers');
10 eval_ok('(eq? 1 2)', '0', 'neq numbers');
11 eval_ok('(eq? 1 "1")', '0', 'neq numbers and strings');
12 eval_ok("(eq? 1 'a)", '0', 'neq numbers and symbols');
13 eval_ok("(eq? 1 (list 1))", '0', 'neq numbers and lists');
14
15 eval_ok('(eq? "a" "a")', '1', 'eq strings');
16 eval_ok('(eq? "a" "b")', '0', 'neq strings');
17 eval_ok('(eq? "1" 1)', '0', 'neq strings and numbers');
18 eval_ok('(eq? "a" \'a)', '0', 'neq strings and symbols');
19 eval_ok('(eq? "a" (list "a"))', '0', 'neq strings and lists');
20
21 eval_ok("(eq? 'a 'a)", '1', 'eq symbols');
22 eval_ok("(eq? 'a 'b)", '0', 'neq symbols');
23 eval_ok("(eq? 'a 1)", '0', 'neq symbols and numbers');
24 eval_ok('(eq? \'a "a")', '0', 'neq symbols and strings');
25 eval_ok("(eq? 'a (list 'a))", '0', 'neq symbols and lists');
26
27 eval_ok("(eq? (list 1 2) (list 1 2))", '1', 'eq lists');
28 eval_ok("(eq? (list 1 2) (list 1 2 3))", '0', 'neq lists');
29 eval_ok("(eq? (list 1) 1)", '0', 'neq lists and numbers');
30 eval_ok('(eq? (list "a") "a")', '0', 'neq lists and strings');
31 eval_ok("(eq? (list 'a) 'a)", '0', 'neq lists and symbols');
32
33 eval_ok("(eq? () ())", '1', 'eq empty lists');
34 eval_ok("(eq? () (list 1))", '0', 'neq empty lists');
35 eval_ok("(eq? 1 1 1 1)", '1', 'eq multiple arguments');
36 eval_ok("(eq? 1 1 1 2)", '0', 'neq multiple arguments');
37
38 eval_ok("(< 1 2 3 4)", '1', '< multiple arguments');
39 eval_ok("(< 1 2 3 3)", '0', '!< multiple arguments');
40
41 eval_ok("(<= 1 2 3 3)", '1', '<= multiple arguments');
42 eval_ok("(<= 1 2 3 2)", '0', '!<= multiple arguments');
43
44 eval_ok("(> 4 3 2 1)", '1', '> multiple arguments');
45 eval_ok("(> 4 3 2 2)", '0', '!> multiple arguments');
46
47 eval_ok("(>= 4 3 2 2)", '1', '>= multiple arguments');
48 eval_ok("(>= 4 3 2 3)", '0', '!>= multiple arguments');
49
50 eval_ok("(and 1 2 3)", "3", 'and success');
51 eval_ok("(and 1 2 () 3)", "()", 'and failure');
52
53 eval_ok("(or 1 2 3)", "1", 'or success');
54 eval_ok("(or 0 0 3 0)", "3", 'or success [2]');
55 eval_ok("(or 0 0 0 0)", "0", 'or failure');
56
The next set of tests in
Listing 31 exercizes the new repl itself
ensuring that the appropriate error messages are produced
after various requests for backtracking, and that the repl
recovers gracefully in all situations.
Listing 31. t/AMB_repl.t 1 use strict;
2 use warnings;
3 use Test::More;
4 use lib './t/lib';
5 use PScm::Test tests => 2;
6
7 BEGIN { use_ok('PScm') }
8
9 eval_ok(<<EOT, <<EOR, 'sequential repl and amb');
10 1
11 ? ?
12 +1
13 (amb 'x 'y 'z)
14 ? ? ? ?
15 (list (amb 1 2) (amb 5 6))
16 ? ? ?
17 (list (amb 1 2) (amb 5 6))
18 (list (amb 1 2) (amb 5 6))
19 EOT
20 1
21 Error: no more solutions
22 Error: no current problem
23 1
24 x
25 y
26 z
27 Error: no more solutions
28 Error: no current problem
29 (1 5)
30 (1 6)
31 (2 5)
32 (2 6)
33 (1 5)
34 (1 5)
35 EOR
36
The last set of tests, in
Listing 32
gives amb a thorough workout.
It tests most of the examples that we have seen in this chapter,
plus a few more for good measure. Additionally, it tests that
set! and define do in fact undo their assignments
in the face of backtracking
Listing 32. t/AMB_amb.t 1 use strict;
2 use warnings;
3 use Test::More;
4 use lib './t/lib';
5 use PScm::Test tests => 8;
6
7 BEGIN { use_ok('PScm') }
8
9 my $prereqs = <<EOT;
10 (define require
11 (lambda (x)
12 (if x x (amb))))
13
14 (define member?
15 (lambda (item lst)
16 (if lst
17 (if (eq? item (car lst))
18 1
19 (member? item (cdr lst)))
20 0)))
21
22 (define distinct?
23 (lambda (lst)
24 (if lst
25 (if (member? (car lst)
26 (cdr lst))
27 0
28 (distinct? (cdr lst)))
29 1)))
30
31 (define one-of
32 (lambda (lst)
33 (begin
34 (require lst)
35 (amb (car lst) (one-of (cdr lst))))))
36
37 (define exclude
38 (lambda (items lst)
39 (if lst
40 (if (member? (car lst) items)
41 (exclude items (cdr lst))
42 (cons (car lst)
43 (exclude items (cdr lst))))
44 ())))
45
46 (define abs
47 (lambda (x)
48 (if (< x 0)
49 (- x)
50 x)))
51
52 (define not
53 (lambda (x)
54 (if x 0 1)))
55
56 (define xor
57 (lambda (x y)
58 (or (and x (not y))
59 (and y (not x)))))
60
61 (define difference
62 (lambda (a b)
63 (abs (- a b))))
64
65 (define divisible-by
66 (lambda (n)
67 (lambda (v)
68 (begin
69 (define test
70 (lambda (o)
71 (if (eq? o v)
72 1
73 (if (> o v)
74 0
75 (test (+ o n))))))
76 (test 0)))))
77
78 (define even?
79 (lambda (a)
80 ((divisible-by 2) a)))
81 EOT
82
83 my $prereqs_output = <<EOT;
84 require
85 member?
86 distinct?
87 one-of
88 exclude
89 abs
90 not
91 xor
92 difference
93 divisible-by
94 even?
95 EOT
96
97 $prereqs_output =~ s/\n$//s;
98
99
100 eval_ok(<<EOT, <<EOR, 'even?');
101 $prereqs
102 (define test
103 (lambda ()
104 (let ((x (amb 1 2 3 4 5)))
105 (begin
106 (require (even? x))
107 x))))
108 (test)
109 ?
110 ?
111 EOT
112 $prereqs_output
113 test
114 2
115 4
116 Error: no more solutions
117 EOR
118
119 eval_ok(<<EOT, <<EOR, 'Barrels of Fun');
120 $prereqs
121 (define some-of
122 (lambda (lst)
123 (begin
124 (require lst)
125 (amb (list (car lst))
126 (some-of (cdr lst))
127 (cons (car lst)
128 (some-of (cdr lst)))))))
129
130 (define sum
131 (lambda (lst)
132 (if lst
133 (+ (car lst)
134 (sum (cdr lst)))
135 0)))
136
137 (define barrels-of-fun
138 (lambda ()
139 (let* ((barrels (list 30 32 36 38 40 62))
140 (beer (one-of barrels))
141 (wine (exclude (list beer) barrels))
142 (barrel1 (one-of wine))
143 (barrel2 (one-of (exclude (list barrel1) wine)))
144 (barrels (some-of (exclude (list barrel1 barrel2) wine))))
145 (begin
146 (require (eq? (* 2 (+ barrel1 barrel2))
147 (sum barrels)))
148 beer))))
149 (barrels-of-fun)
150 EOT
151 $prereqs_output
152 some-of
153 sum
154 barrels-of-fun
155 40
156 EOR
157
165
166 eval_ok(<<EOT, <<EOR, 'amb');
167 $prereqs
168
169 (define multiple-dwelling
170 (lambda ()
171 (let* ((baker (one-of (list 1 2 3 4)))
172 (cooper (one-of (exclude (list baker) (list 2 3 4 5))))
173 (fletcher (one-of (exclude (list baker cooper) (list 2 3 4))))
174 (miller (one-of (exclude (list baker cooper fletcher)
175 (list 1 2 3 4 5))))
176 (smith (car (exclude (list baker cooper fletcher miller)
177 (list 1 2 3 4 5)))))
178 (begin
179 (require (> miller cooper))
180 (require (not (eq? (difference smith fletcher) 1)))
181 (require (not (eq? (difference cooper fletcher) 1)))
182 (list (list 'baker baker)
183 (list 'cooper cooper)
184 (list 'fletcher fletcher)
185 (list 'miller miller)
186 (list 'smith smith))))))
187
188 (multiple-dwelling)
189 EOT
190 $prereqs_output
191 multiple-dwelling
192 ((baker 3) (cooper 2) (fletcher 4) (miller 5) (smith 1))
193 EOR
194
195 eval_ok(<<EOF, <<EOR, 'Liars (optimized)');
196 $prereqs
197 (define liars
198 (lambda ()
199 (let* ((betty (amb 1 2 3 4 5))
200 (ethel (one-of (exclude (list betty)
201 (list 1 2 3 4 5))))
202 (joan (one-of (exclude (list betty ethel)
203 (list 1 2 3 4 5))))
204 (kitty (one-of (exclude (list betty ethel joan)
205 (list 1 2 3 4 5))))
206 (mary (car (exclude (list betty ethel joan kitty)
207 (list 1 2 3 4 5)))))
208 (begin
209 (require (xor (eq? kitty 2) (eq? betty 3)))
210 (require (xor (eq? ethel 1) (eq? joan 2)))
211 (require (xor (eq? joan 3) (eq? ethel 5)))
212 (require (xor (eq? kitty 2) (eq? mary 4)))
213 (require (xor (eq? mary 4) (eq? betty 1)))
214 '((betty ,betty)
215 (ethel ,ethel)
216 (joan ,joan)
217 (kitty ,kitty)
218 (mary ,mary))))))
219 (liars)
220 ?
221 EOF
222 $prereqs_output
223 liars
224 ((betty 3) (ethel 5) (joan 2) (kitty 1) (mary 4))
225 Error: no more solutions
226 EOR
227
228 eval_ok(<<EOF, <<EOR, 'set! backtracking');
229 (let ((x 1))
230 (let ((y (amb 'a 'b)))
231 (begin
232 (print (list 'x x))
233 (set! x 2)
234 (print (list 'x x))
235 y)))
236 ?
237 EOF
238 (x 1)
239 (x 2)
240 a
241 (x 1)
242 (x 2)
243 b
244 EOR
245
246 eval_ok(<<EOF, <<EOR, 'define backtracking');
247 (define x 1)
248 (let ((y (amb 'a 'b)))
249 (begin
250 (print (list 'x x))
251 (define x 2)
252 (print (list 'x x))
253 y))
254 ?
255 EOF
256 x
257 (x 1)
258 (x 2)
259 a
260 (x 1)
261 (x 2)
262 b
263 EOR
264
265 eval_ok(<<EOT, <<EOR, 'parsing');
266 $prereqs
267
268 (define proper-nouns '(john paul))
269 (define nouns '(car garage))
270 (define auxilliaries '(will has))
271 (define verbs '(put))
272 (define articles '(the a his))
273 (define prepositions '(in to with))
274 (define degrees '(very quite))
275 (define adjectives '(red green old new))
276
277 (define parse-sentance
278 (lambda ()
279 (amb (list (parse-noun-phrase)
280 (parse-word auxilliaries)
281 (parse-verb-phrase))
282 (list (parse-noun-phrase)
283 (parse-verb-phrase)))))
284
285 (define parse-noun-phrase
286 (lambda ()
287 (amb (parse-word proper-nouns)
288 (list (parse-word articles)
289 (parse-adj-phrase)))))
290
291 (define parse-adj-phrase
292 (lambda ()
293 (amb (list (parse-deg-phrase)
294 (parse-adj-phrase))
295 (parse-word nouns))))
296
297 (define parse-deg-phrase
298 (lambda ()
299 (amb (list (parse-word degrees)
300 (parse-deg-phrase))
301 (parse-word adjectives))))
302
303 (define parse-verb-phrase
304 (lambda ()
305 (list (parse-word verbs)
306 (parse-noun-phrase)
307 (parse-prep-phrase))))
308
309 (define parse-prep-phrase
310 (lambda ()
311 (list (parse-word prepositions)
312 (parse-noun-phrase))))
313
314 (define parse-word
315 (lambda (words)
316 (begin
317 (require *unparsed*)
318 (require (member? (car *unparsed*) words))
319 (let ((found-word (car *unparsed*)))
320 (begin
321 (set! *unparsed* (cdr *unparsed*))
322 found-word)))))
323
324 (define *unparsed* ())
325
326 (define parse
327 (lambda (input)
328 (begin
329 (set! *unparsed* input)
330 (let ((sentance (parse-sentance)))
331 (begin
332 (require (not *unparsed*))
333 sentance)))))
334
335 (parse '(john will put his car in the garage))
336 (parse '(paul put a car in his garage))
337 (parse '(paul has put a very very old car in his quite new red garage))
338 EOT
339 $prereqs_output
340 proper-nouns
341 nouns
342 auxilliaries
343 verbs
344 articles
345 prepositions
346 degrees
347 adjectives
348 parse-sentance
349 parse-noun-phrase
350 parse-adj-phrase
351 parse-deg-phrase
352 parse-verb-phrase
353 parse-prep-phrase
354 parse-word
355 *unparsed*
356 parse
357 (john will (put (his car) (in (the garage))))
358 (paul (put (a car) (in (his garage))))
359 (paul has (put (a ((very (very old)) car)) (in (his ((quite new) (red garage))))))
360 EOR
361