Continuations

What are continuations? Why should you want to know about them? The rest of this chapter is devoted to answering the first of those questions, but the second question deserves some sort of an answer early on, if only to encourage you to pursue the answer to the first.

I hope you can remember (I certainly do) that wonderful eureka moment when you first “got” recursion, and all its implications. Grasping the concept of continuations is an even more rewarding and dare I say transcendental experience, and well worth the effort.

Continuations are an advanced control-flow technique that can be used to implement any and all standard control-flow mechanisms including but not limited to conditional branching, loops (with break statements), goto, return etc. Beyond the standard control-flow mechanisms, continuations also promise an almost limitless potential for new types of control flow that might be difficult or near impossible to achieve in any other way, for example

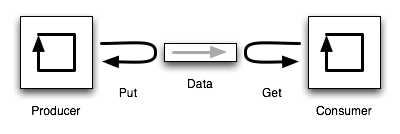
Let's talk a bit about co-routines. Co-routines are groups of two or more functions or methods that interact with one another in a much more even-handed way than just “A() calls B().” A classic example is a producer-consumer pair of routines, which pass data, possibly via some intermediate structure such as a list. The producer produces data, pushing it on to the list, and the consumer consumes it, shifting it off the list again, something like Figure 13.1.

Think of the producer using some complex algorithm to generate a stream of data while the consumer uses an equally complex algorithm to parse it. Both the producer and consumer are independant loops, so on the face of it, if the producer was called it would never relinquish control to give the consumer a look-in, it would just continue to push data onto that list. Likewise the consumer, if it were running, would just consume data until the list was exhausted. Both loops could have extensive internal logic and state such that even if the producer could simply call the consumer when it had produced something, the consumer would have great difficulty returning control to the producer without loosing all of its internal state. Reversing the roles, so that the consumer called the producer would still have exactly the same issues.

The only apparent solution would be to implement the producer and the consumer as separate threads, or even as completely separate processes and have some IPC mechanism to pass the data between them. But this pair of co-routines might only be part of a much larger system and the division into separate threads or processes might be inelegant or inappropriate. Continuations provide a solution by allowing a sort of “procedural goto” wherby control passes directly from the center of one routine to the heart of the other, and then back again, resuming exactly where the “goto” left off!

Threads are a common enough concept nowadays, but you might be surprised to hear that continuations make it almost trivial to implement so called “green” threads (application as opposed to operating system threads). We'll actually do this in a later chapter.

Exceptions are a simple application of continuations, where control, rather than unwinding down a stack, proceeds immediately to some handler routine. Perl's eval{die} construct is an example of this sort of thing. We'll demonstrate a very simple error construct towards the end of this chapter.

Logic Programming, as demonstrated by languages such as Prolog [pip], is a completely different paradigm; it has more in common with recursive database search and large-scale pattern matching than the mostly functional style of programming presented by PScheme. However a more advanced application of continuations makes it possible to implement the basis of such a language, and we will attempt that later on too.

I hope that I have whet your appetite for the potential of continuations, however the topic of continuations is somewhat difficult, and this chapter is a long one.

Before diving in, it would be a good idea to discuss a couple of related topics, namely tail recursion and tail call optimization. Then with those under our belts, we can progress to continuations themselves. We will talk about continuations by discussing continuation passing style, a programming technique available to many languages, including Perl. Then we proceed to re-write the interpreter from Chapter 12 in continuation passing style, and by exposing the underlying continuations in the PScheme language, we show what an incredibly powerful tool they are.

Much of the above may not make much sense on first reading, but hopefully the rest of the chapter will make it clear, so let's get started.

13.1. Tail Recursion and Tail Call Optimization

Consider the following definition of factorial() in Perl:

sub factorial {
    my ($n) = @_;
    if ($n == 0) {
        return 1;
    } else {
        return $n * factorial($n - 1);
    }
}

print factorial(5), "\n";  # prints 120
[download]

This is the classic recursive definition of the factorial function: the factorial of 0 is 1, and the factorial of any other positive number is that number times the factorial of one less than that number (factorial is not defined for negative numbers). You will be getting very familiar with this function in various guises from here on in so it is probably worth taking a good long look at it now in its simplest form before we start to change things.

To start off, consider the behaviour of this function when called with a positive numeric argument. The evolution on the stack of the call to factorial(5) would proceed as follows:

factorial(5)
5 * factorial(4)
5 * 4 * factorial(3)
5 * 4 * 3 * factorial(2)
5 * 4 * 3 * 2 * factorial(1)
5 * 4 * 3 * 2 * 1 * factorial(0)
5 * 4 * 3 * 2 * 1 * 1
5 * 4 * 3 * 2 * 1
5 * 4 * 3 * 2
5 * 4 * 6
5 * 24
120

Although this picture omits many details, it is obvious that the stack grows (to the right in the example) and that there are deferred multiplications that only get performed as the calls to factorial() return and the stack is unwound again.

We can rewrite that factorial function in a different form with the addition of a helper function, like this:

sub factorial {
    my ($n) = @_;
    return factorial_helper($n, 1);
}

sub factorial_helper {
    my ($n, $result) = @_;
    if ($n == 0) {
        return $result;
    } else {
        return factorial_helper($n - 1, $n * $result);
    }
}

print factorial(5), "\n";  # still prints 120
[download]

This version works by moving the body of the factorial function into the helper function and passing it an additional value, an accumulator with an initial value of 1. This means that the helper function can calculate the result as it proceeds up the stack rather than having to wait for $n to reach zero and calculating the result on the way back down.

This is still a recursive definition, but because of the way the result is calculated it differs from the original factorial() in one absolutely crucial detail: the last thing it does is to call itself recursively and it immediately returns the result. In the original definition the result of the recursive call to factorial() had to be multiplied by the current value of $n before it could be returned.

A function which is called and its result immediately returned is said to be in tail position and the code making the call is said to be making a tail call. A recursive function which calls itself in tail position is said to be tail recursive. Tail calls are special because the stack setup to make the call and teardown afterwards is essentially redundant: the result of the function making the tail call is the result of the function being called, and the caller's stack frame is destroyed immediatly after the called function's stack frame is. If we could overwrite the caller's arguments with the arguments to the called function, then goto the called function, then when that function does a return it will return not to the caller, but to the caller of the caller. This is called tail-call optimization (TCO).

Figure 13.2 shows a normal procedure call in tail postion. You can see that the stack is extended by the called function's frame (which includes the return address), then that extension is discarded as the called function returns, then the calling function's frame is subsequently discarded as the calling function returns to the previous caller (we are talking about the Perl stack here, not PScheme environments).

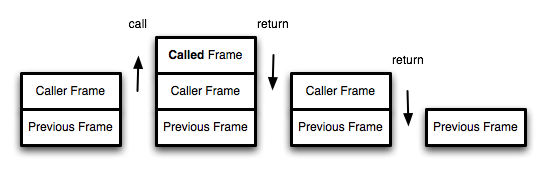
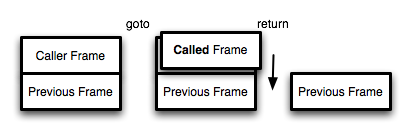
Figure 13.2. Tail call without TCO

Figure 13.3 shows the effect of tail call optimization. The caller's frame is replaced by the called function's frame, then the caller jumps to the called function. When the called function returns it does so directly to the previous caller.

Figure 13.3. Tail call with TCO

Perl allows us to do precisely this, by means of assignment to @_ and the special goto &sub syntax. Here's our factorial_helper() again, this time with TCO:

sub factorial_helper {
    my ($n, $result) = @_;
    if ($n == 0) {
        return $result;
    } else {
        @_ = ($n - 1, $n * $result);
        goto \&factorial_helper;
    }
}
[download]

This function, although written in a recursive style, operates in a constant space and consumes no stack. In fact it is pretty much equivalent to this iterative definition:

sub factorial_helper {
    my ($n, $result) = @_;
  REPEAT:
    if ($n == 0) {
        return $result;
    } else {
        --$n; $result *= $n;
        goto REPEAT;
    }
}
[download]

which just emphasizes the point that TCO'd tail-calls are really just gotos with arguments.

Many language implementations (gcc springs to mind) can perform implicit TCO, detecting calls in tail position and replacing the call with a goto, and that's all calls in tail position, not just recursive ones. Furthermore, some languages such as Scheme require this behaviour of their implementations³². Our PScheme implementation, through the use of continuations, will by the end of this chapter support something equivalent.

That's really all there is to tail recursion and TCO³³. I've already said they have a direct bearing on continuations, but there is a lot more to continuations than that, so lets take a look at using continuations in perl.

13.2. Continuation Passing Style

This section discusses continuation passing style (CPS). It contains a number of exclaimation marks; I hope you will agree that they are justified.

One way of thinking about a procedural computation is by decomposing it into just two main operations:

Calling a function with arguments;
Returning a result from a function.

Continuation passing style eliminates the second of these operations; in pure continuation passing style no function you call ever returns!

This page deliberately left blank to allow time for reflection on the enormity of the previous statement.

...That being the case, you need to figure out how to tell a CPS function what to do with its result. So, since a CPS function can't return a result, it is instead passed an additional procedure as argument: a continuation, and it passes its result to that.

The continuation represents the remainder of the computation after a function “returns”. Since calling a continuation is equivalent to returning a result in non-CPS, you can also think of a continuation as a reference to your function's return statement.

As you might imagine, a computation which never returns will simply consume stack indefinately, until it completes, but I hope the discussion of TCO above has addressed some of your reservations on that score, and as I've said, continuations themselves, when fully realised, provide an alternative mechanism for dealing with the same issue.

So what does continuation passing style look like in Perl? Well since continuations are procedures, closures are an obvious and easy way to implement them. So our continuations can be created by sub { ... } and called by $continuation->(...).

For a first example of CPS transformation, we'll go back to our original factorial() function from Section 13.1 and re-write it in CPS. To save you having to refer back to it, here it is again.

sub factorial {
    my ($n) = @_;
    if ($n == 0) {
        return 1;
    } else {
        return $n * factorial($n - 1);
    }
}

print factorial(5), "\n";  # prints 120
[download]

Now as we have said, all CPS functions take an additional continuation argument. The continuation we pass it depends on what we want to do with the result. Our original example printed the result, so let's just pass a continuation to do that:

factorial(5, sub { print shift, "\n" });
[download]

The additional continuation argument sub { print shift, "\n" } just takes one argument and prints it.

Next up is factorial() itself. This CPS factorial() takes an additional continuation as argument, so the first couple of lines are easy:

sub factorial {
    my ($n, $cont) = @_;
[download]

Next remember that whenever the function used to return a result, it must now call its continuation on that result, so the next couple of lines are also pretty easy: wheras the original returned 1 if $n was 0, the CPS version calls its continuation on the value 1 instead.

if ($n == 0) {
    $cont->(1);
[download]

This works for factorial(0, sub { print shift, "\n" } ): the continuation will get and print a 1.

That leaves the tricky bit. The original function reads:

} else {
    return $n * factorial($n - 1);
}
[download]

You can see that recursive call to factorial() has some deferred computation, namely the multiplication by $n to be done when the call returns. But as we've said a CPS function never returns so we must somehow wrap that deferred computation up in a new continuation and pass it to factorial().

If you get stuck on a difficult CPS transform, it almost always pays to break the expression into a sequence of simpler operations first. We can do that here easily enough:

} else {
    my $factorial_result = factorial($n - 1);
    my $result = $n * $factorial_result;
    return $result;
}
[download]

So this is much easier now. You can see that the first thing that happens is that factorial() calls itself. Then the result is multiplied by $n, and finally it is returned. So our new continuation is just the code that now follows the call to factorial(), wrapped in a function:

sub {
    my ($factorial_result) = @_;
    my $result = $n * $factorial_result;
    return $result;
}
[download]

Since factorial() will call this continuation with its result, $factorial_result is the argument to the continuation.

There is one additional change that we need to make. Where the original code did a return $result, our new continuation must call the original continuation on the $result instead.

sub {
    my ($factorial_result) = @_;
    my $result = $n * $factorial_result;
    $cont->($result);
}
[download]

This is our new continuation. All that remains is to pass it to our recursive factorial call:

} else {
    factorial($n - 1, sub {
            my ($factorial_result) = @_;
            my $result = $n * $factorial_result;
            $cont->($result);
        }
    );
}
[download]

We can now shorten this considerably by eliminating the temporary variables:

} else {
    factorial($n - 1, sub { $cont->($n * shift) });
}
[download]

The new continuation is sub { $cont->($n * shift) }. It takes one argument: the result so far (this is the value that our non-CPS factorial() would have returned). It multiplies the result by the current value of $n then calls the current continuation $cont on that value³⁴.

That completes our initial CPS re-implementation of factorial():

sub factorial {
    my ($n, $cont) = @_;
    if ($n == 0) {
        $cont->(1);
    } else {
        factorial($n - 1, sub { $cont->($n * shift) });
    }
}

factorial(5, sub { print shift, "\n" });  # still prints 120
[download]

At the risk of labouring a point, consider the call:

factorial(3, sub { print shift, "\n" });
[download]

The evolution of the continuation will proceed as follows:

sub {
    print shift, "\n"
}

sub {
    sub {
        print shift, "\n"
    }->(3 * shift)
}

sub {
    sub {
        sub {
            print shift, "\n"
        }->(3 * shift)
    }->(2 * shift)
}

sub {
    sub {
        sub {
            sub {
                print shift, "\n"
            }->(3 * shift)
        }->(2 * shift)
    }->(1 * shift)
}

sub {
    sub {
        sub {
            sub {
                print shift, "\n"
            }->(3 * shift)
        }->(2 * shift)
    }->(1 * shift)
}->(1)  # factorial 0

sub {
    sub {
        sub {
            print shift, "\n"
        }->(3 * shift)
    }->(2 * shift)
}->(1)

sub {
    sub {
        print shift, "\n"
    }->(3 * shift)
}->(2)

sub {
    print shift, "\n"
}->(6)

print 6, "\n"
[download]

The deferred multiplications accumulate until we reach the point where the entire accumulated continuation is finally called with argument 1, then they unwind from the outside in until the original continuation gets invoked on the argument 6 and 6 is printed. If you think about it, this evolution is functionally identical with the implicit deferred computations on the stack in our original factorial(), the only difference being that now we have a variable $cont that explicitly refers to the continuation.

Still sticking with our CPS factorial(), there is more that we can do. Because in CPS no function ever returns, all function calls must be in tail position!³⁵. As you can see our recursive call to factorial() is now in tail position, so we can use TCO to remove the spurious use of stack:

sub factorial {
    my ($n, $cont) = @_;
    if ($n == 0) {
        $cont->(1);
    } else {
        @_ = ($n - 1, sub { $cont->($n * shift) });
        goto \&factorial;
    }
}
[download]

This is still a “recursive” definition of factorial(), but now it is not the stack which is growing, but the continuation itself which consumes more and more space as our computation proceeds.

An astute reader will have realised that, in fact, we are still using stack when the continuations actually get triggered: those calls to $cont->($n * shift) will of course use just as much stack as the original did. However note that the continuations themselves must be called in tail position, so with a little more work we can eliminate that stack overhead too:

sub factorial {
    my ($n, $cont) = @_;
    if ($n == 0) {
        @_ = (1);
        goto $cont;
    } else {
        @_ = ($n - 1, sub { @_ = ($n * shift); goto $cont; });
        goto \&factorial;
    }
}
[download]

This is very messy, but it works as advertised: it consumes absolutely no stack at any point; all deferred computations are in the continuations. Just bear in mind that in a language that provided implicit TCO, we wouldn't need any of those assignments to @_ or the gotos, and I've promised that continuations themselves will allow an alternative and cleaner solution in our interpreter.

Moving on, what about that iterative/recursive definition of factorial() with a helper function from Section 13.1? We can re-write that in CPS too. How does it compare? Well first here's a non-CPS variation on the original again, thoroughly TCO'd this time:

sub factorial {
    my ($n) = @_;
    @_ = ($n, 1);
    goto \&factorial_helper;
}

sub factorial_helper {
    my ($n, $result) = @_;
    if ($n == 0) {
        return ($result);
    } else {
        @_ = ($n - 1, $n * $result);
        goto \&factorial_helper;
    }
}

print factorial(5), "\n";  # prints 120
[download]

and here it is re-written in CPS:

sub factorial {
    my ($n, $cont) = @_;
    @_ = ($n, 1, $cont);
    goto \&factorial_helper;
}

sub factorial_helper {
    my ($n, $result, $cont) = @_;
    if ($n == 0) {
        @_ = ($result);
        goto $cont;
    } else {
        @_ = ($n - 1, $n * $result, $cont);
        goto \&factorial_helper;
    }
}

factorial(5, sub { print shift, "\n" });  # still prints 120
[download]

Our new tail recursive CPS factorial() function takes an additional continuation argument and passes that to factorial_helper(). factorial_helper() either goes to the continuation with the result, or goes to itself with new values for $n and $result; but since it has no deferred computation, it does not need to construct a new continuation and just passes the existing continuation to the recursive call.

The take home message here is that this tail recursive definition of factorial() using factorial_helper() translates into a CPS where neither the stack nor the continuation grows. This is a general result: functions written to be tail-recursive consume no stack when TCO'd, and do not build new continuations when rewritten into CPS.

The “normal” way, or at least the easiest way to produce CPS code is to do what we did above: take non-CPS code and translate it into CPS. In the next section we're going to look at a few examples of simple, hypothetical function forms and how they translate into CPS.

13.3. Example CPS Transformations

To keep these examples simple, we'll ignore any issues of TCO. These examples should allow us to proceed with more confidence into the subsequent rewrite of our interpreter.

The simplest kind of function is one that takes no arguments and returns a constant:
```
sub A {
    return 'hello';
}
[download]
```
The CPS form of this takes a continuation as argument and calls the continuation on the constant:
```
sub A {
    my ($ret) = @_;

    $ret->('hello');
}
[download]
```
I've called the continuation $ret instead of $cont to emphasize it's equivalence with a return statement. One of the guiding principles of converting to CPS is that calling the argument continuation in CPS is equivalent to doing a return in non-CPS. In fact you can mentally substitute return(...) for $ret->(...) in many of these examples without disturbing the sense of them.
The next simplest form is a function that takes arguments and performs only primitive operations such as addition on them, returning the result:
```
sub A {
    my ($x, $y) = @_;

    return $x + $y;
}
[download]
```
In this case, since primitive operations can't take a continuation, and because they are “terminal” operations that won't run away off up the stack, we again can just call the continuation on the result:
```
sub A {
    my ($x, $y, $ret) = @_;

    $ret->($x + $y);
}
[download]
```
Next come simple functions that just call another function without any deferred computation:
```
sub A {
    my ($x) = @_;

    return B($x);
}
[download]
```
Here, since there is no deferred computation, there need be no new continuation, we just pass the existing continuation to the called function:
```
sub A {
    my ($x, $ret) = @_;

    B($x, $ret);
}
[download]
```
This is just saying to B() “return your result here.”
Now we're starting to get into areas where there is deferred computation, and this is where it starts to get just a little bit tricky:
```
sub A {
    return C(B());
}
[download]
```
B() gets called first, and the value it returns is passed as argument to C(). In CPS B() would never return so we must also call it first, passing it a new continuation that calls C() with B()'s result and the current continuation:
```
sub A {
    my ($ret) = @_;

    B(
        sub {
            my ($B_result) = @_;
            C($B_result, $ret);
        }
    );
}
[download]
```
The new continuation calls C() with two arguments: the result of the call to B(), and the original continuation $ret to which C() should return its result. Since the original call to C() was returned as the result of the call to A(), C() is being told “return your result here”.
Sequential function calls present a slightly different problem.
```
sub A {
    B();
    C();
    D();
}
[download]
```
Here we must construct a nest of continuations to ensure that C() and D() get called in the correct order after B():
```
sub A {
    my ($ret) = @_;
    B(
        sub {
            C(
                sub{
                    D($ret);
                }
            );
        }
    );
}
[download]
```
We call B() with a continuation that will call C() with a continuation that will call D() with the original continuation $ret since the result of the call to D() was the result of the original call to A(). Again this is just saying to D() “return your result here.”
Next let's look at a conditional expression:
```
sub A {
    my ($x) = @_;

    if (B($x)) {
        C($x);
    } else {
        D($x);
    }
}
[download]
```
The call to B() in the condition will never return, so we must pass it a continuation that tests its result and decides which branch to take accordingly, passing the the original continuation to the chosen branch:
```
sub A {
    my ($x, $ret) = @_;

    B($x,
        sub {
            my ($B_result) = @_;
            if ($B_result) {
                C($x, $ret);
            } else {
                D($x, $ret);
            }
        }
    );
}
[download]
```
Both the true and the false branch used to make a single call in tail position to C() or D(), so now we simply pass the original continuation unchanged as an additional argument to C() or D().
Finally, for now, lets look at a looping function.
```
sub A {
    my $i = 0;
    while ($i < 10) {
        B();
        ++$i;
    }
}
[download]
```
This needs a bit more thought. It turns out to be easiest to do a preliminary rewrite of this example into a recursive form as follows:
```
sub A {
    A_h(0);
}

sub A_h {
    my ($i) = @_;
    if ($i < 10) {
        B();
        A_h($i + 1);
    }
}
[download]
```
Turning that into CPS then becomes just a re-application of examples we've seen before:
```
sub A {
    my ($ret) = @_;
    A_h(0, $ret);
}

sub A_h {
    my ($i, $ret) = @_;
    if ($i < 10) {
        B(
            sub { A_h($i + 1, $ret); }
        );
    }
}
[download]
```
A() calls A_h() with the continuation unchanged (A_h(), return your result here.) Since B() will not return, it is passed a continuation that carries on the recursion on A_h(), passing the original continuation $ret.

The examples above give a taste of the sorts of transformations that we shall be applying to our interpreter soon. There are other more difficult cases that might appear impossible at first sight (uses of map for example,) but again they can be resolved by first re-writing the expressions in a more tractable form before converting to CPS. We'll see examples of this sort of thing when we get to them.

It happens that there does exist a formal methodology for transforming statements in any language capable of supporting CPS into CPS. The above example transformations are samples from that ruleset. All such transformations can be automated. When I started this chapter I was hopeful that perhaps something in the B package, the Perl compiler, would be available that could perform the transform but that appears not to be the case. Anyhow we'll learn a lot more about CPS by performing the transform manually, so that is the best approach to take.

13.4. The Trampoline

I promised that there was an alternative to all the messy assignments to @_ and the gotos that constitute TCO. Well that falls out of three closely related properties of a fully realised CPS:

No function call ever returns, therefore:
Every function call must be in tail position, and therefore:
If you were to return something it would be guaranteed to return all the way down the stack to the originating caller³⁶.

Now just suppose that at well chosen points we do return something, and not just anything. Suppose we return another continuation, this time taking no arguments, that when called just continues the calculation from where it left off!

That is one of the surprising things about continuations, that they are completely self-contained and require no external context to operate. You may need to convince yourself that this will work: Since we can TCO a CPS function, such that it uses no Perl stack at all, then even if the CPS code is not TCO'd there can be nothing on the Perl stack that it actually needs, just a long chain of return adresses that it pases through after the computation is finished. Returning a continuation like this merely interleaves this otherwise laborious chain of returns with the normal flow of control up the stack.

So how do we deal with this returned continuation? A handler routine, called a trampoline, starts off by being called with a continuation of no arguments. It loops, repeatedly calling the continuation and assigning the result (another continuation of no arguments) back to the continuation itself until the result is undef. The code is easier to write than to describe:

sub trampoline {
    my ($cont) = @_;
    $cont = $cont->() while defined $cont;
}
[download]

To give you a feel of how this might work, let's return once more to our CPS factorial() function and re-write it to make use of a trampoline instead of TCO. First to refresh your memory here's our first CPS attempt again (slightly modified) before we TCO'd it:

sub factorial {
    my ($n, $ret) = @_;
    if ($n == 0) {
        $ret->(1);
    } else {
        factorial($n - 1,
                  sub {
                      my ($a) = @_;
                      $ret->($n * $a)
                  });
    }
}

factorial(5, sub { print shift, "\n"; });  # still prints 120
[download]

and here it is rewritten to use a trampoline.

sub factorial {
    my ($n, $ret) = @_;
    if ($n == 0) {
        return sub { $ret->(1); };
    } else {
        return sub {
            factorial($n - 1,
                      sub {
                          my ($a) = @_;
                          return sub { $ret->($n * $a) }
                      });
        };
    }
}

sub trampoline {
    my ($cont) = @_;
    $cont = $cont->() while defined $cont;
}

trampoline(
    sub {
        factorial(5, sub { print shift, "\n"; return undef; });
    }
); # still prints 120
[download]

Changes from the original are in bold as usual. The key to understanding this is to notice that whenever a function call was done in the original, either to factorial() or to the continuation, a closure which will make that call is returned to the trampoline instead. Each time this happens the stack is completely cleared down and the trampoline resumes the computation by calling the returned closure. Finally, at the end of the computation, the original continuation passed to factorial() gets invoked, printing the result and returning undef to the trampoline causing it to stop.

Like TCO, the trampoline technique is not specific to CPS, but both techniques require that the modified calls be in tail position, making CPS a prime candidate for either kind of optimisation³⁷.

Well that's pretty scary stuff. Both TCO and the trampoline are simply alternative strategies to avoid unlimited use of the stack, and you may be wondering if the trampoline has any advantages over TCO at this point. I'd like to make a few arguments in favour of the trampoline here.

Our factorial() example is a very tight piece of code which somewhat overemphasizes the role of the trampoline by doing a lot with it in a small space. Particularily the explicit return of a closure to make the recursive call does not have to be done for every tail call, we just need to ensure it happens fairly regularily on our way up the stack. For example in a set of mutually tail recursive subroutines, A() calling B() calling C() calling A()..., only one of those subroutines need do that return. This is in contrast to TCO, where any unoptimised tail call constitutes a permanently unclaimed stack frame.
Some languages do not allow the possibility of doing TCO, so any CPS implementation using such a language would have to use a trampoline.
We can hide the trampoline from client CPS code by representing continuations as objects which contain the closures, and putting the return to the trampoline in the method that invokes the closure (provided that method is invoked in tail position).

It is the third argument that swings the case, and that's exactly what we'll be doing. If you don't get that argument yet, hold on and it will be made clear later.

13.5. Using CPS

Thinking back to our original exposition of CPS from Section 13.2 where we suggested that normal procedural programming consisted primarily of calling functions and returning values, we said that CPS eliminates the second of these two operations. In fact that was a slight oversimplification. There is a certain amount of equivalence between the operations of “call” and “return”, it is just the direction of the flow of data that differs, “upwards” to the called function via its arguments, versus “downwards” from the called function via its return value. Continuation passing style in fact unifies these two operations, returning a value is the same as calling a function. Since in CPS data flows in only one direction, in some sense CPS is actually a simplification!

Furthermore, an application written in CPS with complete TCO needs no stack at all: TCO allows us to eliminate the use of stack by tail calls, and in CPS all function calls are tail calls³⁸.

So now you understand continuations, but how do you use them? Well at each step of a computation you have a continuation representing the current function's return statement. But a continuation is a variable, a reference to a subroutine, and you can do whatever you like with it!. You don't have to call it (return through it) just when everyone is expecting you to, you might call (return through) a completely different continuation instead, or you might pass it to another function that can call it (return through it) if it likes. And when a continuation is called (returned through), control flow transfers to wherever the return statement equivalent to that continuation would have returned! Put another way, you have always had control over what value your function returns, and when it returns it, but not until now have you had control over where it returns it to!

And there's more. Although code written in CPS retains the notion of a stack since functions call functions and return values (via continuations); as we've already noted the stack is not really relevant, or even necessarily present. Any continuation is as valid as any other. It is perfectly permissable to call a continuation that resumes control in a function that has already returned, in effect jumping across the call graph that a stack based language is constrained by!

Let's give an explicit example to illustrate this last point. Consider the following simple perl script:

sub A {
    print "in A\n";
    B();
    print "back in A\n";
}

sub B {
    print "    in B\n";
    C();
    print "    back in B\n";
}

sub C {
    print "        in C\n";
}

sub X {
    print "in X\n";
    Y();
    print "back in X\n";
}

sub Y {
    print "    in Y\n";
    Z();
    print "    back in Y\n";
}

sub Z {
    print "        in Z\n";
}

A();
X();
[download]

A() calls B() which calls C(), and X() calls Y() which calls Z(). The top level calls A() then X(). You shouldn't take too long to convince yourself that it will produce the following output:

in A
    in B
        in C
    back in B
back in A
in X
    in Y
        in Z
    back in Y
back in X
[download]

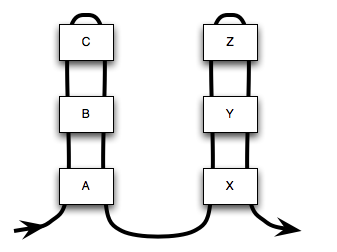
Just to hammer home the simple point, Figure 13.4 shows the thread of control flow passing through A(), B(), C(), X(), Y() and Z().

Figure 13.4. Control flow for the simple script

Now let's re-write that program into CPS, without changing any of it's behaviour:

sub A {
    my ($ret) = @_;
    print "in A\n";
    B(sub { $ret->(print "back in A\n") });
}

sub B {
    my ($ret) = @_;
    print "    in B\n";
    C(sub { $ret->(print "    back in B\n") });
}

sub C {
    my ($ret) = @_;
    $ret->(print "        in C\n");
}

sub X {
    my ($ret) = @_;
    print "in X\n";
    Y(sub { $ret->(print "back in X\n") });
}

sub Y {
    my ($ret) = @_;
    print "    in Y\n";
    Z(sub { $ret->(print "    back in Y\n") });
}

sub Z {
    my ($ret) = @_;
    $ret->(print "        in Z\n");
}

A(sub { X(sub {})});
[download]

There are no new tricks that haven't already been described in Section 13.3 above, the only difference is that since none of the original functions actually returned anything interesting (they returned the results of print statements), the equivalent continuations don't bother looking at their arguments.

This produces identical output to the original program, and exhibits exactly the same control flow. Now let's make just three tiny changes.

my $C_ret;

sub A {
    my ($ret) = @_;
    print "in A\n";
    B(sub { $ret->(print "back in A\n") });
}

sub B {
    my ($ret) = @_;
    print "    in B\n";
    C(sub { $ret->(print "    back in B\n") });
}

sub C {
    my ($ret) = @_;
    $C_ret = $ret;
    $ret->(print "        in C\n");
}

sub X {
    my ($ret) = @_;
    print "in X\n";
    Y(sub { $ret->(print "back in X\n") });
}

sub Y {
    my ($ret) = @_;
    print "    in Y\n";
    Z( sub { $ret->(print "    back in Y\n") });
}

sub Z {
    my ($ret) = @_;
    $C_ret->(print "        in Z\n");
}

A(sub { X(sub {})});
[download]

The first change is to declare a $C_ret variable to hold a continuation. Then C(), before it calls its continuation, stores it in this $C_ret variable. Finally Z(), instead of calling its own continuation $ret, calls the saved continuation $C_ret instead.

This produces the output below. Whether or not you find this surprising will depend on how closely you've been following the discussion:

in A
    in B
        in C
    back in B
back in A
in X
    in Y
        in Z
    back in B
back in A
in X
    in Y
        in Z
    back in B
back in A
in X
    in Y
        in Z
    back in B
back in A
...
[download]

All proceeds normally until we reach the first call to Z(). Since Z() calls the continuation that C() saved, Z() instead of returning to X(), returns to B() instead. Then normal service is resumed, starting from the return to B(), until the next return from Z(), which again returns to B() and so on, ad infinitum. what we have achieved is the control flow shown in Figure 13.5.

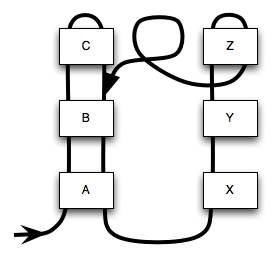
Figure 13.5. Control flow with continuations

(Cue the Mony Python music.)

If this still isn't clear, which I suspect may be the case, look at Figure 13.6. In this figure I've “broken apart” the functions from their continuations. A() calls B() calls C() which calls the continuation of B() (e.g. cB()) which calls the continuation of A() etc. Now the continuation of B() is just “return to A()” (call cA()) and the continuation of A() is to call X() etc.

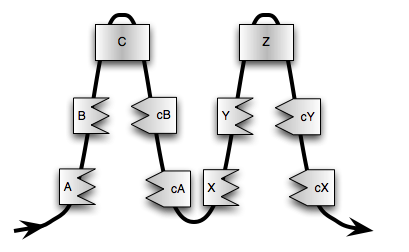
Figure 13.6. Continuations are just (anonymous) subroutines

I'm deliberately down-playing the idea of “return” now, this really is just function calls, and in that case Figure 13.7 shows that there is really nothing special about Z calling cB, it's just a recursive loop, and TCO or a trampoline will take care of the stack for us.

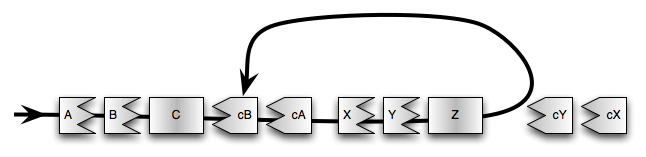
Figure 13.7. Continuations really are just subroutines

This is what I meant by saying that CPS is a simplification. It linearizes control flow, so that it is just a straight line of function calls. Once you get that idea, a whole world of possibilities opens up. For instance you can probably imagine at this stage that with a little more work, adding loops and passing continuations around, we could easily arrive at a coroutine implementation, where control does jump from the heart of one loop to the heart of another and back again without disturbing the state of either loop.

There is a big downside to writing in CPS however, and that is that it makes your head hurt. A far better approach is to use a language that has continuations built in “under the hood”. Then when you write “return $val” you are really calling a continuation on $val, but you don't have to worry about it, and when you need to get hold of a continuation, you can ask for one. A language like that provides continuations as first class objects in that they can be passed around as variables, much in the same way as Perl provides anonymous subroutines (closures) as first class objects.

For example, if Perl had built-in continuations, and we could get at the current continuation by i.e. taking a reference to the return keyword³⁹, then we could rewrite all of this example without CPS, as follows:

my $cont;

sub A {
    print "in A\n";
    B();
    print "back in A\n";
}

sub B {
    print "    in B\n";
    C();
    print "    back in B\n";
}

sub C {
    $cont = \return;
    print "        in C\n";
}

sub X {
    print "in X\n";
    Y();
    print "back in X\n";
}

sub Y {
    print "    in Y\n";
    Z();
    print "    back in Y\n";
}

sub Z {
    print "        in Z\n";
    $cont->()
}

A();
X();
[download]

Bold text shows the differences from the original non-CPS version.

We are going to turn our PScheme interpreter into just such a language. The next few sections will describe the changes we need to make.

13.6. Implementation

Rather than attempting to rewrite the interpreter of Chapter 12 from start to finish in CPS, We're going to backtrack to our first “interesting” interpreter, from Chapter 5 which has only let and lambda, and re-implement that. This has the advantage that we get a real working interpreter with continuations which we can test early on, and we can demonstrate some of the power of continuations with it. Then I'll gloss the re-writing of the final interpreter in stages by working through the intermediate versions pausing only to study any previously unencountered constructs that require novel treatment. Finally we'll have a continuation-passing version of the interpreter from Chapter 12 to play with.

13.6.1. Our Trampoline Implementation

Our implementation of the trampoline does not differ significantly from the example that we presented for factorial() above. But it is still best introduced gradually, so this section is still pseudocode, to a certain extent.

Firstly we need to rewrite the read-eval-print loop into CPS, so that we can call the whole thing from the trampoline. This isn't actually very difficult to do, the repl for version 0.0.2 conceptually is as simple as

sub repl {
    my ($reader, $outfh) = @_;
    while (my $expr = $reader->read()) {
        my $result = $expr->Eval(new env);
        $result->Print($outfh);
    }
}
[download]

We've already seen in Section 13.3 that the easiest way to transform a while loop into CPS is first to rewrite it into a recursive form, and this is easy to do here:

sub repl {
    my ($reader, $outfh) = @_;
    if (my $expr = $reader->read()) {
        my $result = $expr->Eval(new env);
        $result->Print($outfh);
        repl($reader, $outfh);
    }
}
[download]

Now to recast that into CPS is fairly trivial, especially if we remember that the reader PScm::Read::Read() already returns undef on EOF, and it can continue to do so, telling the trampoline to stop, and only calling its continuation if there is something to evaluate.

sub repl {
    my ($reader, $outfh, $ret) = @_;
    $reader->read(
        sub {
            my ($expr) = @_;
            $expr->Eval(
                new env,
                sub {
                    my ($result) = @_;
                    $result->Print(
                        $outfh,
                        sub { repl($reader, $outfh, $ret) }
                    )
                }
            )
        }
    )
}
[download]

So apart from the return of undef by the reader, where would we put these return statements that return a continuation to the trampoline? Well as I've said we could place them throughout the code, but there's a better idea.

Instead of continuations being simple anonymous subroutines, we make them into objects that contain those anonymous subroutines, with a Cont() method to invoke the underlying closure. Then instead of just writing:

$ret->($arg);
[download]

to invoke a continuation, we say:

$ret->Cont($arg);
[download]

Then, in that Cont() method, instead of just saying

sub Cont {
    my ($self, $arg) = @_;
    $self->{cont}->($arg);
}
[download]

we instead write

sub Cont {
    my ($self, $arg) = @_;
    return sub { $self->{cont}->($arg) };
}
[download]

we have both effected the return of a continuation to the trampoline, and completely hidden the fact from the client code⁴⁰!

In reality there are a few minor complications with this approach, but the above discussion is very close to our final implementation.

13.6.2. CPS `let` and `lambda`

In this section we re-implement the interpreter version 0.0.2 from Chapter 5 in continuation passing style. Once that is done, we introduce a new construct, call/cc, which allows the language direct access to continuations.

First of all we need a new PScm::Continuation class. I don't want to show you all of that class just yet, but here's its new() method:

 13 sub new {
 14     my ($class, $cont) = @_;
 15     bless { cont => $cont }, $class;
 16 }

It takes an anonymous subroutine as argument and stores it in a cont field. We don't want to be writing new PScm::Continuation( sub {...} ) all over the place, so we sweeten things with a little syntactic sugar:

 18 sub cont(&) {
 19     my ($cont) = @_;
 20     return __PACKAGE__->new($cont);
 21 }

This is put on PScm::Continuation's @EXPORT list⁴¹ so after importing it with “use PScm::Continuation;”, instead of writing new PScm::Continuation( sub {...} ) we just write cont {...} instead. If you're not familiar with this technique, see [pp pp225–231].

As discussed above, we add a trampoline() subroutine to PScm which repeatedly invokes the continuation returned from its previous invocation, until the invocation returns undef, signaling the end of the computation. Here's trampoline():

 70 sub trampoline {
 71     my ($cont) = @_;
 72     $cont = $cont->Bounce() while defined $cont;
 73 }

It's functionally equivalent to the prototype trampoline() subroutine discussed above. The Bounce() method is defined in PScm::Continuation to immediately invoke the continuation with no arguments:

 39 sub Bounce {
 40     my ($self) = @_;
 41     $self->{cont}->();
 42 }

Only trampoline() calls Bounce().

Now we need to look at the Read-Eval-Print loop from PScm, with the trampoline in place.

 32 sub ReadEvalPrint {
 33     my ($infh, $outfh) = @_;
 34 
 35     $outfh ||= new FileHandle(">-");
 36     my $reader = new PScm::Read($infh);
 37     trampoline(cont { repl($reader, $outfh) });
 38 }

It's the same as we've seen before up to Line 37 where instead of entering it's loop, it invokes the trampoline with a continuation. That continuation invokes a new helper routine repl() with the reader and the current output handle as arguments. Here's repl().

 40 sub repl {
 41     my ($reader, $outfh) = @_;
 42     $reader->Read(
 43         cont {
 44             my ($expr) = @_;
 45             $expr->Eval(
 46                 new PScm::Env(
 47                     let    => new PScm::SpecialForm::Let(),
 48                     '*'    => new PScm::Primitive::Multiply(),
 49                     '-'    => new PScm::Primitive::Subtract(),
 50                     if     => new PScm::SpecialForm::If(),
 51                     lambda => new PScm::SpecialForm::Lambda(),
 52                     'call/cc' =>
 53                       new PScm::SpecialForm::CallCC(),
 54                 ),
 55                 cont {
 56                     my ($result) = @_;
 57                     $result->Print(
 58                         $outfh,
 59                         cont {
 60                             repl($reader, $outfh);
 61                         }
 62                     )
 63                 }
 64             )
 65         }
 66     )
 67 }

So the guts of the old ReadEvalPrint() have been moved to repl(). It's just an expansion of the CPS pseudocode for repl() in the previous section, and not nearly as bad as it might first appear, it's really just Read() calling Eval() calling Print() calling repl(), all through passed continuations.

There is also something new added to the environment. we'll see what that new binding call/cc on Line 53 is about later.

So the Read(), Eval() and Print() methods now all take continuations and must be modified accordingly. Thankfully the modifications to Read() and Print() are trivial.

First we need to look at the CPS Print() method.

 75 sub Print {
 76     my ($expr, $outfh, $cont) = @_;
 77     print $outfh $expr->as_string, "\n";
 78     $cont->Cont($expr);
 79 }

It just does what it used to do, then calls its continuation with an arbitrary argument. That is the continuation that will restart the repl and it doesn't actually expect an argument, but Cont() does so we're just playing nice.

Notice that on Line 77 we don't pass a continuation to the as_string() method. This is just a normal non-CPS method call. The reasoning behind that is that although as_string() is potentially recursive, at no point will it cause evaluation of any PScheme expressions. Since we are only interested in continuations that might be exposed to user code, we can classify any method call that cannot result in a call to Eval() as a simple expression and deal with it as an atomic operation. Contrarywise, calls to Eval() or calls to methods that might result in a call to Eval() are classified as significant expressions, and must be rewritten into CPS. This distinction makes our rewrite much simpler⁴².

As described above, that Cont() method actually returns a continuation of zero arguments which the trampoline will execute (by calling Bounce() on it). This is the trick I was enthusing about earlier: to return a continuation to the trampoline that will call the current continuation, rather than just directly calling the current continuation. The return will fall all the way back to the trampoline, effecting a complete cleardown of whatever stack might have accumulated up to this point, then the trampoline will kick things off again:

 34 sub Cont {
 35     my ($self, $arg) = @_;
 36     return cont { $self->{cont}->($arg) };
 37 }

The really neat thing about this is that the code that is written to use this method neither knows nor cares that the continuation is not simply being invoked directly at this point. The presence of the trampoline is completely invisible to the client CPS code.

Let's take a look at Read() in PScm::Read next. In fact what we have done is to rename Read() to _read(), leaving it otherwise unchanged:

 17 sub _read {
 18     my ($self) = @_;
 19 
 20     my $token = $self->_next_token();
 21     return undef unless defined $token;
 22 
 23     return $token unless $token->is_open_token;
 24 
 25     my @res = ();
 26 
 27     while (1) {
 28         $token = $self->_read;
 29         die "unexpected EOF"
 30           if !defined $token;
 31         last if $token->is_close_token;
 32         push @res, $token;
 33     }
 34 
 35     return new PScm::Expr::List(@res);
 36 }

Then we provide a new Read() that handles the continuation.

 63 sub Read {
 64     my ($self, $cont) = @_;
 65     my $res = $self->_read();
 66     return undef unless defined $res;
 67     $cont->Cont($res);
 68 }

Read() collects the result of the call to _read(), and if it is undef signifying EOF it returns undef to the trampoline telling it to stop. Otherwise it calls its continuation on the result.

Next we need to take a look at Eval().

All Eval() methods now also take an additional continuation as argument. All the Eval() methods are in subclasses of PScm::Expr. Let's start by looking at the simplest of those expressions: literals and symbols.

The old Eval() method in PScm::Expr just returned $self (numbers, strings and anything else by default evaluate to themselves). The new version is little different, it calls its argument continuation on itself:

 12 sub Eval {
 13     my ($self, $env, $cont) = @_;
 14     $cont->Cont($self);
 15 }

Now for PScm::Expr::Symbol::Eval(). The old Eval() method in PScm::Expr::Symbol returned $env->LookUp($self). Our CPS version calls its continuation on that result instead, because we can treat the call to LookUp() as a simple expression:

103 sub Eval {
104     my ($self, $env, $cont) = @_;
105     $cont->Cont($env->LookUp($self));
106 }

Evaluation of lists is a little more tricky, so to refresh our memories here's the original PScm::Expr::List::Eval() before CPS transformation:

 62 sub Eval {
 63     my ($self, $env) = @_;
 64     my $op = $self->first()->Eval($env);
 65     return $op->Apply($self->rest, $env);
 66 }

On Line 64 It evaluates the first component of the list to get the operator $op, then on Line 65 it applies the operation $op to the rest of the unevaluated list.

Here's the CPS form:

 63 sub Eval {
 64     my ($self, $env, $cont) = @_;
 65     return cont {
 66         $self->first()->Eval(
 67             $env,
 68             cont {
 69                 my ($op) = @_;
 70                 $op->Apply($self->rest, $env, $cont);
 71             }
 72         );
 73     };
 74 }

There's rather a lot going on here, so best we approach it in two stages.

Firstly the return cont { ... } block wraps the entire method body in a continuation that we return to the trampoline. Apart from PScm::Continuation::Cont() this is the only other place where we explicitly fall back down to the trampoline. This is because all recursive calls to Eval() and Apply() must pass through this single function, and so we can stop all runaway stack consumption by Eval() and Apply() here⁴³. You can just ignore the return cont wrapper and consider only the body of the continuation as if it were the body of the function. It would still work, but might run out of stack in the long run.

Secondly inside the method proper we assume that the first call to Eval(), in order to to get the $op, will not return, so we pass it a continuation which accepts the result $op, and applies it to the rest of the list, passing in the original continuation (Line 70). We must pass the original continuation $cont to Apply(), rather than just calling the continuation on the result of the Apply(), because the Apply() might make calls to Eval() to evaluate arguments to the $op, among other things, and must therefore be rewritten in CPS.

So that's it for the rewrite of all of the Eval() methods in PScm::Expr. Now we need to follow the chain of continuation passing into the various Apply() methods we have. Since this is an early version of the interpreter, there aren't too many, in fact they are in:

PScm::Primitive;
PScm::SpecialForm::Let;
PScm::SpecialForm::If;
PScm::SpecialForm::Lambda and
PScm::Closure::Function.

Starting with PScm::Primitive::Apply(), you'll remember that all primitive operations share a common Apply() method. Now individual primitives do not have to accept continuations because they are terminal operations, so all that we have to do is to call the continuation that was passed to the shared primitive Apply() on the result of applying the individual primitive to its arguments.

Unfortunately this is complicated by the fact that the primitive Apply() must first evaluate its arguments. The original primitive Apply() did it with map:

  7 sub Apply {
  8     my ($self, $form, $env) = @_;
  9 
 10     my @unevaluated_args = $form->value;
 11     my @evaluated_args = map { $_->Eval($env) } @unevaluated_args;
 12     return $self->_apply(@evaluated_args);
 13 }

This is a little tricky to rewrite in CPS, so we're going to attack it in stages. Stage one will be to write a recursive version of the builtin map, which instead of taking a sub and list, takes a listref and an environment, and for each element of the listref, calls that element's Eval() method with the environment as argument, accumulating the result in a new listref. But wait a minute, don't we already have such a recursive map_eval() method? Yes, we wrote just such a method when we implemented true list processing for version 0.0.5 back in Section 8.5.1.

Here's that method again.

120 sub map_eval {
121     my ($self, $env) = @_;
122     return $self->Cons($self->[FIRST]->Eval($env),
123                        $self->[REST]->map_eval($env));
124 }

Now remember that that is code from 0.0.5, and here we're just rewriting version 0.0.2, so we don't have true list processing yet, lots of our methods are still expecting Perl array references, we don't have a Cons() method, and we don't have any PScm::Expr::List::Null class. Nonetheless we can cast this method back in to 0.0.2 terms quite easily.

This 0.0.2 map_eval() method is not yet in CPS form:

sub map_eval {
    my ($self, $env) = @_;
    if (@$self) {
        return [ $self->first->Eval($env),
                 @{ $self->rest->map_eval($env) } ];
    } else {
        return [];
    }
}
[download]

This is pretty straightforward.

The second stage of our attack is to re-write map_eval() in CPS. It will take an additional continuation argument, then, much as our factorial() example did, if the recursion has reached its limit (the argument list is empty) it calls its continuation on the empty list. Otherwise it has not finished, and it evaluates its first component, passing a continuation that arranges to evaluate the rest of the list by recursing:

 76 sub map_eval {
 77     my ($self, $env, $cont) = @_;
 78 
 79     if (@$self) {
 80         $self->first->Eval(
 81             $env,
 82             cont {
 83                 my ($evaluated_first) = @_;
 84                 $self->rest->map_eval(
 85                     $env,
 86                     cont {
 87                         my ($evaluated_rest) = @_;
 88                         $cont->Cont([$evaluated_first,
 89                                      @$evaluated_rest]);
 90                     }
 91                 );
 92             }
 93         );
 94     } else {
 95         $cont->Cont([]);
 96     }
 97 }

This is the trickiest piece of code in the entire CPS re-write. Fortunately having done it, it is useful in a number of other scenarios. Now that we have map_eval() we can use it to re-write PScm::SpecialForm::Primitive::Apply():

  8 sub Apply {
  9     my ($self, $form, $env, $cont) = @_;
 10 
 11     $form->map_eval(
 12         $env,
 13         cont {
 14             my ($ra_evaluated_args) = @_;
 15             $cont->Cont($self->_apply(@$ra_evaluated_args));
 16         }
 17     );
 18 }

Not too bad. The map_eval() is passed a continuation that applies the primitive operation to the evaluated arguments and calls the original argument continuation on the result.

It is worth noting again that there was no need to pass any continuation to the individual private _apply() methods for each primitive, so PScm::Primitive::Multiply etc. are unchanged.

The rest of the CPS transformations are much simpler, on the whole, and others that require the rewriting of map can make use of map_eval().

Next up is PScm::SpecialForm::Let, here's the changes:

 13 sub Apply {
 14     my ($self, $form, $env, $cont) = @_;
 15 
 16     my ($bindings, $body) = $form->value;
 17     my (@symbols, @values);
 18 
 19     foreach my $binding ($bindings->value) {
 20         my ($symbol, $value) = $binding->value;
 21         push @symbols, $symbol;
 22         push @values,  $value;
 23     }
 24 
 25     $env->Extend(
 26         \@symbols,
 27         \@values,
 28         cont {
 29             my ($newenv) = @_;
 30             $body->Eval($newenv, $cont);
 31         }
 32     );
 33 }

The changes are in bold on Lines 14 and 27–31

If you remember, the old version at the end simply said

return $body->Eval($env->Extend(\@symbols, \@values));
[download]

Since we know that the call to $env->Extend() will not return (those @values are still to be evaluated), we instead have to pass a continuation that will accept the resulting extended environment and evaluate the body in it. We have already dealt with all the Eval() methods (They're all in PScm::Expr) and they all take a continuation, so we pass the original continuation argument, since the Eval() is the expression that this Apply() was previously returning.

Remembering to add PScm::Env::Extend() to our list of methods that will need looking at, we proceed to PScm::SpecialForm::If::Apply(). We've already discussed how to transform a conditional expression into CPS form, but since this is our first encounter in the wild, let's refresh our memory by first looking at the original non-cps version:

 32 sub Apply {
 33     my ($self, $form, $env) = @_;
 34 
 35     my ($condition, $true_branch, $false_branch) = $form->value;
 36 
 37     if ($condition->Eval($env)->isTrue) {
 38         return $true_branch->Eval($env);
 39     } else {
 40         return $false_branch->Eval($env);
 41     }
 42 }

It evaluates the condition in the current env, and calls isTrue() on the result, then uses that to decide whether to evaluate the true branch or the false branch, both in the current environment.

Our CPS version is not that different:

 41 sub Apply {
 42     my ($self, $form, $env, $cont) = @_;
 43 
 44     my ($condition, $true_branch, $false_branch) = $form->value;
 45 
 46     $condition->Eval(
 47         $env,
 48         cont {
 49             my ($result) = @_;
 50             if ($result->isTrue) {
 51                 $true_branch->Eval($env, $cont);
 52             } else {
 53                 $false_branch->Eval($env, $cont);
 54             }
 55         }
 56     );
 57 }

It evaluates the condition in the current environment and passes a continuation that will accept the result. That continuation calls isTrue() on the result and uses that to decide, in exactly the same way, whether to evaluate the true branch or the false branch. In either case the original continuation that was argument to PScm::SpecialForm::If::Apply() is passed to the chosen branch's Eval() method.

Staying with the program, our next task is the invocation of lambda handled by PScm::SpecialForm::Lambda::Apply():

 65 sub Apply {
 66     my ($self, $form, $env, $cont) = @_;
 67 
 68     my ($args, $body) = $form->value;
 69 
 70     $cont->Cont(PScm::Closure::Function->new($args, $body, $env));
 71 }

There's nothing very interesting here. lambda just creates a closure. There are no calls to Eval() that it must make during this creation, so we can treat the call to new as a simple expression and invoke our argument continuation on the result.

That just leaves PScm::Closure::Function::Apply() and PScm::Env::Extend(). Let's start with PScm::Closure::Function. The original just mapped Eval() over its arguments then called a private _apply() method on the results:

 43 sub Apply {
 44     my ($self, $form, $env) = @_;
 45 
 46     my @evaluated_args = map { $_->Eval($env) } $form->value;
 47     return $self->_apply(@evaluated_args);
 48 }

Another job for map_eval() then:

 44 sub Apply {
 45     my ($self, $form, $env, $cont) = @_;
 46 
 47     $form->map_eval(
 48         $env,
 49         cont {
 50             my ($ra_evaluated_args) = @_;
 51             $self->_apply($ra_evaluated_args, $cont);
 52         }
 53     );
 54 }

Note however that we need to pass the current continuation to that private _apply() method. That's because the closure will be calling Eval() on its body. Let's take a look at PScm::Closure::_apply().

 21 sub _apply {
 22     my ($self, $ra_args, $cont) = @_;
 23 
 24     my $extended_env =
 25       $self->env->ExtendUnevaluated([$self->args], $ra_args);
 26     return $self->body->Eval($extended_env, $cont);
 27 }

It differs in that it takes a reference to an array of args and a continuation, rather than just an array of args, and it passes the continuation in to the call to Eval() on its body.

Finally, we need to rewrite PScm::Env::Extend().

 15 sub Extend {
 16     my ($self, $ra_symbols, $ra_values, $cont) = @_;
 17 
 18     PScm::Expr::List->new(@$ra_values)->map_eval(
 19         $self,
 20         cont {
 21             my ($ra_evaluated_values) = @_;
 22             $cont->Cont(
 23                 $self->ExtendUnevaluated(
 24                     $ra_symbols, $ra_evaluated_values
 25                 )
 26             );
 27         }
 28     );
 29 }

It uses map_eval() to evaluate its list of values, passing the result to a continuation that extends the environment with those values. It calls the argument continuation $cont on the result.

At this point in the discussion, we have a working CPS version of interpreter 0.0.2, and all the original tests that were written for that version still pass. However we seem to have done a lot of hard work for no benefit, since the interpreter is externally equivalent to the original 0.0.2 version. We can remedy that by giving the interpreter an additional construct that provides direct access to the underlying continuations.

There are many ways that this could be done, but one of the best-known and most powerful ways is with a form that goes by the unwieldy title call-with-current-continuation, usually abbreviated to call/cc. This form takes a function as argument and calls it, passing the current continuation as an explicit argument to the function, for example:

> (call/cc (lambda (cont) (cont 10)))
10
[download]

When the function invokes the continuation as a function, control returns to the call/cc and the argument to the continuation becomes the result of the call to call/cc.

If the previous example doesn't seem too exciting, how about this:

> (call/cc
>     (lambda (cont)
>         (if (cont 10)
>             20
>             30)))
10
[download]

Here the call to (cont 10) produced an immediate return of the value 10 through the call/cc even though it was executed in the conditional position of an if statement.

These two examples only show control passing down the “stack” when a continuation is invoked. However it is perfectly reasonable for control to return up the stack to a procedure that has already returned. It is simply not easy to demonstrate with this version of the interpreter. Once we have an interpreter with assignment and sequences, it becomes much easier.

call/cc is in fact a low-level, if not the lowest level continuation tool. It is possible to build higher level control constructs using it. Abandoning pscheme for a moment, consider this Fibonacci⁴⁴ sequence generator in some hypothetical Perl-like language that supports co-routines:

sub fib {
    my ($i, $j) = (0, 1);
    for (;;) {
        yield $i;
        ($i, $j) = ($j, $i + $j);
    }
}

while ((my $i = fib()) < 22) { # prints 0 1 2 3 5 8 13 21
    print "$i ";
}
[download]

That yield call not only behaves like a return statement, but also remembers the current state of the function so that the next time the function is called control resumes where it last left off. With built in continuations this sort of control flow is very easy to achieve.

Anyway I hope this has whet your appetite a little for what call/cc can do, so let's have a look at its implementation.

It is of course a special form, and as usual it has an Apply() method:

 74 package PScm::SpecialForm::CallCC;
 75 
 76 use base qw(PScm::SpecialForm);
 77 use PScm::Closure;
 78 use PScm::Continuation;
 79 
 80 sub Apply {
 81     my ($self, $form, $env, $cont) = @_;
 82 
 83     $form->first->Eval(
 84         $env,
 85         cont {
 86             my ($closure) = @_;
 87             $closure->Apply(new PScm::Expr::List($cont),
 88                 $env, $cont);
 89         }
 90     );
 91 }
 92 
 93 1;

It evaluates its first argument, which should result in a function of one argument, passing the Eval() a continuation which will Apply() the function to a form explicitly containing the current continuation. It also passes the current env and the current continuation a second time, this time as the normal implicit argument.

That's all there is to it. Of course the continuation itself will need an Apply() method so that it can be invoked as an operator.

We're now ready to see the whole of the PScm::Continuation package, in Listing 24.

Listing 24. PScm/Continuation.pm

  1 package PScm::Continuation;
  2 
  3 use strict;
  4 use warnings;
  5 use base qw(PScm);
  6 
  7 require Exporter;
  8 
  9 our @ISA = qw(PScm Exporter);
 10 
 11 our @EXPORT = qw(cont);
 12 
 13 sub new {
 14     my ($class, $cont) = @_;
 15     bless { cont => $cont }, $class;
 16 }
 17 
 18 sub cont(&) {
 19     my ($cont) = @_;
 20     return __PACKAGE__->new($cont);
 21 }
 22 
 23 sub Apply {
 24     my ($self, $form, $env, $cont) = @_;
 25     $form->map_eval(
 26         $env,
 27         cont {
 28             my ($ra_evaluated_args) = @_;
 29             $self->Cont($ra_evaluated_args->[0]);
 30         }
 31     );
 32 }
 33 
 34 sub Cont {
 35     my ($self, $arg) = @_;
 36     return cont { $self->{cont}->($arg) };
 37 }
 38 
 39 sub Bounce {
 40     my ($self) = @_;
 41     $self->{cont}->();
 42 }
 43 
 44 sub Eval {
 45     my ($self, $env, $cont) = @_;
 46     $cont->Cont($self);
 47 }
 48 
 49 1;

We've already seen most of this, only the Apply() method is new.

 23 sub Apply {
 24     my ($self, $form, $env, $cont) = @_;
 25     $form->map_eval(
 26         $env,
 27         cont {
 28             my ($ra_evaluated_args) = @_;
 29             $self->Cont($ra_evaluated_args->[0]);
 30         }
 31     );
 32 }

Apply() on Lines 23–32 is another method that makes use of map_eval() to evaluate its arguments. It passes it a continuation that calls itself on the first of its evaluated arguments, totally ignoring the passed-in, current continuation, and effecting transfer of control to whatever context this continuation represents.

And we're done.

Listing 25. t/PScm_CallCC.t

  1 use strict;
  2 use warnings;
  3 use Test::More;
  4 use lib './t/lib';
  5 use PScm::Test tests => 2;
  6 
  7 BEGIN { use_ok('PScm') }
  8 
  9 eval_ok(<<EOF, '10', 'call/cc');
 10 (let ((a (lambda (return)
 11            (if (return (* 2 5))
 12              20
 13              30))))
 14   (call/cc a))
 15 EOF
 16 
 17 # vim: ft=perl

A simple test of call/cc can be seen in Listing 25.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.2.tgz

13.6.3. CPS `letrec`

The interpreter version 0.0.3 back in Chapter 6 introduced letrec (let recursive) which allowed environments to be created in such a way that closures would extend the environment that they were themselves defined in, allowing them to make recursive calls.

This subsection takes the additions to version 0.0.3 and reimplements them in CPS. We're going to start to pick up the pace somewhat from hereon in, but I'll still present all of the changes, starting with the letrec special form itself. Here's the original v3:

 40 sub Apply {
 41     my ($self, $form, $env) = @_;
 42 
 43     my ($ra_symbols, $ra_values, $body) = $self->UnPack($form, $env);
 44 
 45     return $body->Eval(
 46         $env->ExtendRecursively($ra_symbols, $ra_values));
 47 }

The CPS version calls a modified PScm::Env::ExtendRecursively(), passing a continuation that takes the recursively extended environment and evaluates the body in it, passing the original continuation to that Eval().

 49 sub Apply {
 50     my ($self, $form, $env, $cont) = @_;
 51 
 52     my ($ra_symbols, $ra_values, $body) = $self->UnPack($form);
 53 
 54     $env->ExtendRecursively(
 55         $ra_symbols,
 56         $ra_values,
 57         cont {
 58             my ($extended_env) = @_;
 59             $body->Eval($extended_env, $cont);
 60         }
 61     );
 62 }

PScm::Env::ExtendRecursively() calls PScm::Env::ExtendUnevaluated() as a simple expression then calls _eval_values() on the extended environment, passing the original continuation:

 41 sub ExtendRecursively {
 42     my ($self, $ra_symbols, $ra_values, $cont) = @_;
 43 
 44     my $newenv = $self->ExtendUnevaluated($ra_symbols, $ra_values);
 45     $newenv->_eval_values($cont);
 46 }

Here's the new CPS _eval_values():

 48 sub _eval_values {
 49     my ($self, $cont) = @_;
 50     $self->_map_bindings([keys %{ $self->{bindings} }], $cont);
 51 }

It uses a new helper _map_bindings(), where the original _eval_values() just used map. This works in a similar way to map_eval(), evaluating each value in the environment but then assigning the result back to the original binding:

 53 sub _map_bindings {
 54     my ($self, $ra_keys, $cont) = @_;
 55     my (@keys) = @$ra_keys;
 56     if (@keys) {
 57         my $firstkey = shift @keys;
 58         $self->{bindings}{$firstkey}->Eval(
 59             $self,
 60             cont {
 61                 my ($value) = @_;
 62                 $self->{bindings}{$firstkey} = $value;
 63                 $self->_map_bindings([@keys], $cont);
 64             }
 65         );
 66     } else {
 67         $cont->Cont($self);
 68     }
 69 }

Other methods are unchanged so we have completed the CPS rewrite of letrec, and all tests for 0.0.3 still pass in 0.1.3.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.3.tgz

13.6.4. CPS `let*`

The interpreter version 0.0.4 back in Chapter 7 added let*, a shorthand way of creating nested environments providing the appearence of sequential assignment within the bindings of the let* expression. This was a simple addition, the rewrite will be equally simple.

Here's the new PScm::SpecialForm::LetStar::Apply():

 70 sub Apply {
 71     my ($self, $form, $env, $cont) = @_;
 72 
 73     my ($ra_symbols, $ra_values, $body) = $self->UnPack($form);
 74 
 75     $env->ExtendIteratively(
 76         $ra_symbols,
 77         $ra_values,
 78         cont {
 79             my ($extended_env) = @_;
 80             $body->Eval($extended_env, $cont);
 81         }
 82     );
 83 }

Just like letrec (which called a modified PScm::Env::ExtendRecursively(),) this calls a modified ExtendIteratively(), passing a continuation that evaluates the body of the let* in the new environment with the original continuation.

Here's the modifications to PScm::Env::ExtendIteratively():

 48 sub ExtendIteratively {
 49     my ($self, $ra_symbols, $ra_values, $cont) = @_;
 50     my @symbols = @$ra_symbols;
 51     my @values  = @$ra_values;
 52     if (@symbols) {
 53         my $symbol = shift @symbols;
 54         my $value  = shift @values;
 55         $self->Extend(
 56             [$symbol],
 57             [$value],
 58             cont {
 59                 my ($extended) = @_;
 60                 $extended->ExtendIteratively([@symbols], [@values],
 61                     $cont);
 62             }
 63         );
 64     } else {
 65         $cont->Cont($self);
 66     }
 67 }

The old version just iterated over the name/value pairs, creating an additional nested environment each time around the loop and returning the final result. CPS is easier with recursive definitions so this ExtendIteratively() has been recast as a recursive method. It still does the same job, but additionally arranges that the original continuation gets called on the final, extended environment.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.4.tgz

13.6.5. CPS List Processing

Our next iteration of the interpreter, version 0.0.5 back in Chapter 8, added the list manipulation functions quote, list, car, cdr and cons to the language, and additionally changed the internal implementation of PScm::Expr::List from simple perl listrefs to linked lists, making PScm::Expr::List abstract, adding a PScm::Expr::List::Pair class to represent the cons cells, and adding a PScm::Expr::List::Null class to represent the empty list.

Surprisingly, The CPS rewrite of all of this is quite minimal. First, here's the new quote in PScm::SpecialForm::Quote::Apply():

157 sub Apply {
158     my ($self, $form, $env, $cont) = @_;
159     $cont->Cont($form->first);
160 }

The original returned its first argument unevaluated, the CPS form calls its continuation on it. Remember that the quote system was re-written for a later version of the interpreter to support unquote back in Section 9.2.2, so we'll be returning to quote later on, in Section 13.6.6, where we rewrite that rewrite!

The other additional functions: car, cdr, cons and list are all primitives that share an Apply() method that has already been rewritten into CPS in Section 13.6.2.

Among the PScm::Expr classes, the only thing that changes is the map_eval() method. That method was introduced in version 0.0.5 to work with pscheme lists, then re-introduced at an earlier stage of the CPS rewrite, in version 0.1.2, because we needed a recursive alternative to Perl's map. Finally, here, we combine the two implementations. Here's PScm::Expr::List::Pair::map_eval():

130 sub map_eval {
131     my ($self, $env, $cont) = @_;
132 
133     $self->[FIRST]->Eval(
134         $env,
135         cont {
136             my ($evaluated_first) = @_;
137             $self->[REST]->map_eval(
138                 $env,
139                 cont {
140                     my ($evaluated_rest) = @_;
141                     $cont->Cont($self->Cons($evaluated_first,
142                                             $evaluated_rest));
143                 }
144             );
145         }
146     );
147 }

And here's the new default PScm::Expr::map_eval() that terminates the recursion of map_eval() if $self is PScm::Expr::Null, does the right thing if the cdr of the list is not a list, and handles continuations, all in one tiny method:

 34 sub map_eval {
 35     my ($self, $env, $cont) = @_;
 36     $self->Eval($env, $cont);
 37 }

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.5.tgz

13.6.6. CPS `macro` and `unquote`

Version 0.0.6 of our interpreter, from Chapter 9, introduced the macro special form. This special form took arguments in an identical manner to lambda and created a variant type of closure PScm::Closure::Macro. Normal lambda closure evaluation proceeds by evaluating the arguments to the closure then evaluating the body of the closure with those arguments bound. In contrast macro closure evaluation proceeds by evaluating the body of the closure with its unevaluated arguments bound, then re-evaluating the result.

The rewrite into CPS is trivial, first here's the CPS form of PScm::SpecialForm::Macro::Apply():

175 sub Apply {
176     my ($self, $form, $env, $cont) = @_;
177     my ($args, $body) = $form->value;
178     $cont->Cont(PScm::Closure::Macro->new($args, $body, $env));
179 }

Just as with PSCm::SpecialForm::Lambda::Apply(), the creation of the closure can be treated as a simple expression (no calls to Eval()) and the continuation called on the result.

Now PScm::Closure::Macro::Apply():

 62 sub Apply {
 63     my ($self, $form, $env, $cont) = @_;
 64 
 65     $self->_apply(
 66         $form,
 67         cont {
 68             my ($new_form) = @_;
 69             $new_form->Eval($env, $cont);
 70         }
 71     );
 72 }

Here we pass a continuation to the core _apply() method that takes the resulting new form and evaluates that in the current environment with the current continuation as an additional argument. The core _apply() extends the environment with unevaluated arguments, then calls the body of the macro with the new environment and the passed in continuation.

 17 sub _apply {
 18     my ($self, $args, $cont) = @_;
 19 
 20     my $extended_env =
 21       $self->{env}->ExtendUnevaluated($self->{args}, $args);
 22     $self->{body}->Eval($extended_env, $cont);
 23 }

But you get the idea.

That's all there is to the rewrite of the macro extension into CPS. However Chapter 9 also rewrote PScm::SpecialForm::Quote to support the unquote keyword which allows the interpolation of evaluated sub-expressions within a quoted expression. That proves more interesting to recast into CPS.

Let's start at the top by looking at the new CPS version of PScm::SpecialForm::Quote::Apply():

186 sub Apply {
187     my ($self, $form, $env, $cont) = @_;
188     $form->first->Quote($env, $cont);
189 }

So far so good, we just pass the current continuation along with the current environment to the Quote() method of whatever expression we're quoting.

Let's deal with the easy stuff first. PScm::Expr::Quote() used to just return $self, the CPS version calls the continuation on $self instead:

 41 sub Quote {
 42     my ($self, $env, $cont) = @_;
 43     $cont->Cont($self);
 44 }

That leaves PScm::Expr::List::Pair's Quote():

163 sub Quote {
164     my ($self, $env, $cont) = @_;
165     if ($self->[FIRST]->is_unquote) {
166         $self->[REST]->first->Eval($env, $cont);
167     } else {
168         $self->quote_rest($env, $cont);
169     }
170 }

Great! since the calls to both Eval() and quote_rest() are in tail position, it need only pass the continuation along to both. All the Eval() methods have already been dealt with of course, so that leaves quote_rest(). Let's first refresh our memories by looking at the non-CPS original:

142 sub quote_rest {
143     my ($self, $env) = @_;
144     return $self->Cons(
145         $self->[FIRST]->Quote($env),
146         $self->[REST]->quote_rest($env)
147     );
148 }

This is definately not tail recursive. But if we think it through there are no problems. The first thing it does is call Quote() on its first() element, then it calls itself on the rest() of the list, then finally it calls Cons() on those two results. Both the call to Quote() and quote_rest() could potentially result in calls to Eval() so we need to pass continuations to both. We can rewrite it a little first to make the order of operations more explicit:

sub quote_rest {
    my ($self, $env) = @_;

    my $quoted_first = $self->first->Quote($env);
    my $quoted_rest = $self->rest->quote_rest($env);

    return $self->Cons($quoted_first, $quoted_rest);
}
[download]

Now all we do is rewrite that so that the call to Quote() gets a continuation that performs the remaining two operations, including passing a second continuation to quote_rest() that performs the last Cons(). here's the CPS rewrite:

172 sub quote_rest {
173     my ($self, $env, $cont) = @_;
174     $self->[FIRST]->Quote(
175         $env,
176         cont {
177             my ($quoted_first) = @_;
178             $self->[REST]->quote_rest(
179                 $env,
180                 cont {
181                     my ($quoted_rest) = @_;
182                     $cont->Cont(
183                         $self->Cons($quoted_first, $quoted_rest));
184                 }
185             );
186         }
187     );
188 }

It calls Quote() on its first element, passing a continuation (Lines 176–186) that accepts the $quoted_first and then calls quote_rest() on the rest of the elements, passing that a continuation (Lines 180–184) that accepts the $quoted_rest and calls the original continuation on the result of Cons()-ing the $quoted_first and $quoted_rest together.

Finally, as before, where the default PScm::Expr::quote_rest() just returned $self, now it calls its aregument continuation on $self:

 46 sub quote_rest {
 47     my ($self, $env, $cont) = @_;
 48     $cont->Cont($self);
 49 }

That's it for our CPS rewrite of the unquote facility. All other methods are unchanged.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.6.tgz

13.6.7. CPS Sequences and Assignment

Next up are the sequences (begin) and assignment (set!) introduced by interpreter 0.0.7 in Chapter 10. Let's start with sequences and the begin special form.

To recap begin takes a sequence of zero or more expressions and evaluates them in strict left to right order, returning the last result. If given no arguments, in this implementation it returns the empty list. Here's its Apply():

215 sub Apply {
216     my ($self, $form, $env, $cont) = @_;
217     if ($form->is_pair) {
218         $self->apply_next($form, $env, $cont);
219     } else {
220         $cont->Cont($form);
221     }
222 }

The original was iterative. This version has been recast in a recursive mould to make the CPS transform easier and to take advantage of PScm::Expr::List. If the list is empty it calls the continuation on the empty list, otherwise it passes the form, environment and continuation to a helper method apply_next():

224 sub apply_next {
225     my ($self, $form, $env, $cont) = @_;
226 
227     $form->first->Eval(
228         $env,
229         cont {
230             my ($val) = @_;
231             if ($form->rest->is_pair) {
232                 $self->apply_next($form->rest, $env, $cont);
233             } else {
234                 $cont->Cont($val);
235             }
236         }
237     );
238 }

It evaluates the first element of the list, passing a continuation that accepts the result. If there is more of the list to process, it calls itself recursively on the rest of the list, otherwise it calls the original continuation on the $val (the value of the last expression on the list). Note the similarity between this method and map_eval(). The diference is only that apply_next() does not need to construct a new list of all the evaluated results.

Next and last is set!. set! uses PScm::Env::Assign() that was developed for letrec to locate the nearest binding for a symbol and change its value. set! is a special form since it evaluates its second argument (the value) but not its first (the symbol).

197 sub Apply {
198     my ($self, $form, $env, $cont) = @_;
199     my ($symbol, $expr) = $form->value;
200     $expr->Eval(
201         $env,
202         cont {
203             my ($val) = @_;
204             $cont->Cont($env->Assign($symbol, $val));
205         }
206     );
207 }

The CPS rewrite is pretty straightforward. It evaluates the value passing a continuation that will perform the assignment (a simple expression) calling the original continuation on the result.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.7.tgz

13.6.8. CPS `define`

Version 0.0.8 in Chapter 11 finally introduced define, delayed until then for reasons I won't reiterate here. Akin to set!, define takes a symbol and a value and binds the symbol to the value in the current environment. It is a special form since it does not evaluate the symbol. The CPS rewrite of PScm::SpecialForm::Define::Apply() proceeds much as the one for set! did:

246 sub Apply {
247     my ($self, $form, $env, $cont) = @_;
248     my ($symbol, $expr) = $form->value;
249 
250     $expr->Eval(
251         $env,
252         cont {
253             my ($value) = @_;
254             $cont->Cont($env->Define($symbol, $value));
255         }
256     );
257 }

It evaluates the expression, passing a continuation that accepts the result and calls PScm::Env::Define() to bind the result to the symbol in the current environment. We can treat the call to PScm::Env::Define() as a simple expression and just call the original continuation on the result.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.8.tgz

13.6.9. CPS OOP

Version 0.0.9 in Chapter 12 introduced an object-oriented extension to PScheme, by means of the make-class special form and the root parent class. Although there was a fair amount of code added to implement that extension, it turns out that very little of that code needs changing to produce a CPS version. As usual we just have to hunt down the calls to Eval() and ensure that there is a continuation available to pass in. Let's start with PScm::SpecialForm::MakeClass::Apply().

265 sub Apply {
266     my ($self, $form, $env, $cont) = @_;
267 
268     my $parent_expr = $form->first;
269     my $fields = $form->rest->first;
270     my $methods = $form->rest->rest;
271 
272     $parent_expr->Eval(
273         $env,
274         cont {
275             my ($parent_class) = @_;
276             $cont->Cont(
277                 PScm::Class->new(
278                     $parent_class, $fields, $methods, $env
279                 )
280             );
281         }
282     );
283 }

The first thing the old version did was to evaluate the parent expression (the value of the parent class) then use that along with the fields and methods (unevaluated) to create the new class. Our rewrite evaluates the parent expression passing a continuation that will create the class. We can treat the class creation as a simple expression (it makes no further calls to Eval()) and just call the original continuation on the result.

Nothing to follow up on there, so next we turn our attention to the application of a class to arguments, which creates a new object. This is in PScm::Class::Apply():

 33 sub Apply {
 34     my ($self, $form, $env, $cont) = @_;
 35 
 36     my $new_object = $self->make_instance();
 37     $new_object->call_method(
 38         $new_object,
 39         "init", $form, $env,
 40         cont {
 41             $cont->Cont($new_object);
 42         }
 43     );
 44 }

As usual, Apply() now takes a continuation. The old version called make_instance() to create a new instance of the class, then called the init method of the new object with the arguments to the class, then returned the new object. The CPS version can still just call make_instance() as a simple expression, but needs to pass a continuation to call_method() because call_method() will be calling Eval() on both the arguments and the body of the method. The continuation just calls the original continuation on the new object (as if it were returning it).

Remembering that objects in this implementation are just environments, Here's the rewrite of PScm::Env::call_method():

192 sub call_method {
193     my ($self, $this, $method_name, $args, $env, $cont) = @_;
194 
195     if (my $method = $self->_lookup_method($method_name)) {
196         $method->ApplyMethod($this, $args, $env, $cont);
197     } else {
198         $cont->Cont(undef);
199     }
200 }

Hey, this isn't too bad at all. If call_method() finds the method, it calls ApplyMethod() on it, passing the original continuation as an extra argument. Wheras the old version implicitly returned undef if the method was not found, the CPS version must explicitly call the continuation on undef⁴⁵.

Next we need to look at PScm::Closure::Method::ApplyMethod():

 96 sub ApplyMethod {
 97     my ($self, $this, $form, $env, $cont) = @_;
 98 
 99     $form->map_eval(
100         $env,
101         cont {
102             my ($evaluated_args) = @_;
103             $self->_apply(
104                 PScm::Expr::List->Cons($this, $evaluated_args),
105                 $cont);
106         }
107     );
108 }

Again we use map_eval() on the $form (the arguments to the method) to evaluate them, this time passing a continuation that applies the method to its evaluated arguments, using PScm::Expr::List::Cons() to prepend the current object $this to the PScm::Expr::List of arguments to the core PScm::Closure::_apply() method, and passing in the original continuation. We've already discussed that core _apply() method in Section 13.6.2 when we re-wrote lambda.

That just leaves the calling of methods on the objects themselves. Both PScm::Env and PScm::Env::Super have an Apply() method. The one from PScm::Env::Super arranges to pass the current value of this to the called method, otherwise they are very similar. Here's PScm::Env::Apply():

202 sub Apply {
203     my ($self, $form, $env, $cont) = @_;
204 
205     my ($method, $args) = ($form->first, $form->rest);
206     $self->CallMethodOrDie($self, $method, $args, $env, $cont);
207 }

And here's PScm::Env::Super::Apply():

231 sub Apply {
232     my ($self, $form, $env, $cont) = @_;
233 
234     my ($method, $args) = ($form->first, $form->rest);
235     my $this = $env->LookUp(PScm::Expr::Symbol->new("this"));
236     $self->CallMethodOrDie($this, $method, $args, $env, $cont);
237 }

They both now make use of a new support method PScm::Env::CallMethodOrDie() which just does what it says.

209 sub CallMethodOrDie {
210     my ($self, $this, $method, $args, $env, $cont) = @_;
211     $self->call_method(
212         $this,
213         $method->value,
214         $args, $env,
215         cont {
216             my ($res) = @_;
217             if (defined $res) {
218                 $cont->Cont($res);
219             } else {
220                 die "method ", $method->value, " not found\n";
221             }
222         }
223     );
224 }

It calls call_method() on $self and passes a continuation that checks if the result is defined. If the result is defined that means that call_method() sucessfully found the method and invoked it, in which case the original continuation is called on the result. If the result is undef then the method was not found and CallMethodOrDie() lives up to its name.

To make some of the subsequent tests easier I've added a print primitive. It takes a single evaluated argument and calls its Print() method. The only problem to solve is how to tell it about the current output filehandle. Ideally we would create a new PScm::Expr::FileHandle type and install one containing the default output filehandle in the environment for print to find, however it is easier for our limited purposes to just pass the output filehandle to the PScm::SpecialForm::Print constructor. You can see this in the changes to ReadEvalPrint() between 0.0.9 and 0.1.9 here:

 33 sub ReadEvalPrint {
 34     my ($infh, $outfh) = @_;
 35 
 36     $outfh ||= new FileHandle(">-");
 37     my $reader      = new PScm::Read($infh);
 38     my $initial_env;
 39     $initial_env = new PScm::Env(
 40         let          => new PScm::SpecialForm::Let(),
 41         '*'          => new PScm::Primitive::Multiply(),
 42         '-'          => new PScm::Primitive::Subtract(),
 43         '+'          => new PScm::Primitive::Add(),
 44         if           => new PScm::SpecialForm::If(),
 45         lambda       => new PScm::SpecialForm::Lambda(),
 46         list         => new PScm::Primitive::List(),
 47         car          => new PScm::Primitive::Car(),
 48         cdr          => new PScm::Primitive::Cdr(),
 49         cons         => new PScm::Primitive::Cons(),
 50         letrec       => new PScm::SpecialForm::LetRec(),
 51         'let*'       => new PScm::SpecialForm::LetStar(),
 52         eval         => new PScm::SpecialForm::Eval(),
 53         macro        => new PScm::SpecialForm::Macro(),
 54         quote        => new PScm::SpecialForm::Quote(),
 55         'set!'       => new PScm::SpecialForm::Set(),
 56         begin        => new PScm::SpecialForm::Begin(),
 57         define       => new PScm::SpecialForm::Define(),
 58         'make-class' => new PScm::SpecialForm::MakeClass(),
 59         'call/cc'    => new PScm::SpecialForm::CallCC(),
 60         print        => new PScm::SpecialForm::Print($outfh),
 61     );
 62 
 63     $initial_env->Define(
 64         PScm::Expr::Symbol->new("root"),
 65         PScm::Class::Root->new($initial_env)
 66     );
 67     trampoline(cont { repl($initial_env, $reader, $outfh) });
 68 }

The PScm::SpecialForm::Print package is unusual, therefore, in that it has a new() method and creates its own instance, because it needs to save the argument filehandle. Other than that it is a standard CPS special form:

286 package PScm::SpecialForm::Print;
287 
288 use base qw(PScm::SpecialForm);
289 
290 use PScm::Continuation;
291 
292 sub new {
293     my ($class, $outfh) = @_;
294     bless { outfh => $outfh }, $class;
295 }
296 
297 sub Apply {
298     my ($self, $form, $env, $cont) = @_;
299     $form->first->Eval($env, cont {
300             my ($thing) = @_;
301             $thing->Print(
302                 $self->{outfh},
303                 cont {
304                     $cont->Cont($thing)
305                 }
306             );
307     });
308 }
309 
310 1;

PScm::SpecialForm::Print::Apply() invokes its argument $form's Eval() method with the current environment and a continuation that will print the result, then call the original continuation on the evaluated result. So print returns the expression that it printed.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.1.9.tgz

13.7. CPS Without Closures

Perl has made it relatively easy for us to implement CPS by passing closures as continuations, albeit with an object wrapper. We should be glad of that and continue to use this feature. However the question must be asked: how would we go about implementing CPS in a language that does not support closures?

The answer, or one answer in any case is to roll our own closures as separate objects. This would mean a separate class for every occurrence of the cont{} construct in the PScheme source. The object would be initialized with all of the values that the closure referred to, and a method in the class would perform the same duty as the individual closure, referring to those saved values as attributes of $self rather than as lexical variables. Consider the PScm::Expr::List::Eval() method we discussed early on, in its CPS form:

 63 sub Eval {
 64     my ($self, $env, $cont) = @_;
 65     return cont {
 66         $self->first()->Eval(
 67             $env,
 68             cont {
 69                 my ($op) = @_;
 70                 $op->Apply($self->rest, $env, $cont);
 71             }
 72         );
 73     };
 74 }

You can see three continuations in this one method: the continuation $cont passed in as argument, the outer cont{} returned to the trampoline, and the inner cont{} that applies the evaluated $op to the as-yet unevaluated arguments. There is a lot of dependancy on the lexical scope of various variables in this code. If we were going to do this without closures we would have to make all that explicit. Here's an attempt:

sub Eval {
    my ($self, $env, $cont) = @_;
    return new Bouncer(
        new ListEvalFirstCont($self, $env, $cont)
    );
}
[download]

The Bouncer class would cope with any continuations returned to the trampoline, it would have a new() method to capture the argument continuation and a Bounce() method that invoked the captured continuation:

package Bouncer;

sub new {
    my ($class, $cont) = @_;
    bless { cont => $cont }, $class;
}

sub Bounce {
    my ($self) = @_;
    $self->{cont}->Cont();
}
[download]

Then ListFirstEvalCont would need a new() method, and a Cont() method of no arguments, since that is what the Bouncer would call on it it:

package ListEvalFirstCont;

sub new {
    my ($class, $list, $env, $cont) = @_;
    bless {
        list => $list,
        env  => $env,
        cont => $cont,
    }, $class;
}

sub Cont {
    my ($self) = @_;
    $self->{list}->first()->Eval(
        $self->{env},
        new ListEvalRestCont($self->{list},
                             $self->{env},
                             $self->{cont});
    );
}
[download]

You can see that the Cont() method here is doing the same thing that the closure was doing in the original code, but it in turn must create a new ListEvalRestCont object rather than a closure. That ListEvalRestCont would in turn need a new(), and a Cont() method, since that is what the operations Eval() method would call:

package ListEvalRestCont;

sub new {
    my ($class, $list, $env, $cont) = @_;
    bless {
        list => $list,
        env  => $env,
        cont => $cont,
    }, $class;
}

sub Cont {
    my ($self, $op) = @_;
    $op->Apply($self->{list}->rest,
               $self->{env},
               $self->{cont});
}
[download]

And that's not the end of it, since really that last Cont() method should be returning a continuation to the trampoline rather than just calling Apply() directly...

Admittedly this is just first pass untested code to give you an idea, but I'm not writing this just to scare you off. The point to note is that there are three basic things that have to be kept track of when implementing CPS without continuations. One is the current position in the control flow (in this case the list being evaluated.) The second is the current environment: the values of variables that the continuations need to execute; the third is the containing continuation. In fact what the closure implementation makes implicit and effectively hides from us is that there is a chain of continuations, from closure to closure, back to the originating continuation in the repl. This is an important observation. It will greatly simplify the writing of a PScheme compiler later.

There are even some advantages to implementing continuations in this way. Primarily because the chain of continuations is explicit, it can be traversed and searched making all sorts of additional control flow constructs easier to implement. For example a try / throw / catch / resume mechanism need merely traverse back up the continuation chain looking for a catching continuation, invoke it with the originating continuation, and if the catch block could fix the problem it would resume from the instruction after the throw. While this is possible with our existing implementation, it is more tricky.

13.8. CPS Fun

We're done! Let's play around with what we have.

13.8.1. An `error` Handler

There are many uses of call/cc, the simplest is probably the definition of escape procedures, procedures that when called, escape the current context and return control to a containing outer context. The simplest type of escape procedure is error. If at any point in your code you invoke error, the argument error message is printed, the current context is abandoned and control is returned to the top level. For example (pretending we have a divide “/” operator):

> (define div
>   (lambda (numerator denominator)
>     (if denominator
>         (/ numerator denominator)
>         (error "division by zero"))))
div
> (+ (div 2 0) 1)
Error: division by zero
()
>
[download]

The addition never happened. Control returned directly to the top level. Using call/cc, we can define an error escape procedure in the PScheme language itself, without needing to make further changes to the interpreter.

All error has to do is to print its error message and call a continuation that returns control to the top level. So, assuming that top level continuation is already installed as ^escape (I'm just using a caret, “^”, to prefix any continuation names so they stand out,) the error procedure itself is straightforward:

(define error
  (lambda (msg)
    (begin
      (print msg)
      (^escape ()))))
[download]

Note that the ^escape continuation expects an argument, so error passes the empty list (), and that is what the repl prints as the result of whatever expression error is called from.

Next we need to create that top level continuation. Here's a first attempt:

(define ^escape (call/cc (lambda (c) c)))
[download]

This looks promising. The call/cc calls the anonymous lambda expression passing in the current continuation. The lambda expression just returns its argument, which is what call/cc returns, and that is what gets bound to the global ^escape. This is good, as far as it goes, the current continuation certainly is bound to ^escape.

The problem is that the operation of defining ^escape is part of the continuation saved in ^escape. Put another way, the first time error calls ^escape, control resumes at the point that call/cc is returning its value and so the define is re-executed, binding the empty list to ^escape and forgetting the previously bound continuation. So the ^escape continuation is only useable once.

There are two ways to fix this.

The first way would be to change error so that it passes ^escape as argument to itself: (^escape ^escape), The downside of that is that you will get a PScm::Continuation printed out as the result of any call to error.

The other way to fix this is to change the way we set up ^escape in the first place. First of all we create a global ^escape variable with an arbitrary initial binding:

(define ^escape 0)
[download]

Then we use call/cc as before but call an expression that directly assigns to ^escape:

(call/cc
  (lambda (cont)
    (begin
      (set! ^escape cont))))
[download]

This way the call/cc has no enclosing context, no deferred operations to perform, and when ^escape is invoked control returns directly to the top level.

A test of the error handler, which just duplicates the above code, is in Listing 26.

Listing 26. t/CPS_Error.t

  1 use strict;
  2 use warnings;
  3 use Test::More;
  4 use lib 't/lib';
  5 use PScm::Test tests => 2;
  6 
  7 BEGIN { use_ok('PScm') }
  8 
  9 eval_ok(<<EOF, <<EOR, 'error');
 10 (define ^error 0)
 11 (call/cc
 12   (lambda (cont)
 13     (begin
 14       (set! ^error cont))))
 15 
 16 (define error
 17   (lambda (msg)
 18     (begin
 19       (print msg)
 20       (^error ()))))
 21 
 22 (define div
 23   (lambda (numerator denominator)
 24     (if denominator
 25         (/ numerator denominator)
 26         (error "division by zero"))))
 27 
 28 (+ (div 2 0) 1)
 29 
 30 EOF
 31 ^error
 32 PScm::Continuation
 33 error
 34 div
 35 "division by zero"
 36 ()
 37 EOR
 38 
 39 # vim: ft=perl

Next let's try something a bit more challenging.

13.8.2. `yield`

Remember that strange Fibonacci generator that was described towards the end of Section 13.6.2, the one that used a hypothetical yield command to return a value while remembering its current position so that a subsequent call to the function would resume where it left off? Well here's how we'd like to write it in PScheme:

(define fib
  (yielder
    (letrec ((fib-loop
               (lambda (i j)
                 (begin
                   (yield i)
                   (fib-loop j (+ i j))))))
      (fib-loop 0 1))))
[download]

and here's how we'd like to call it:

(let ((n 10))
  (while n
    (begin
      (set! n (- n 1))
      (print (fib)))))
[download]

Note that there is nothing at all special about the code that uses fib. All of the interesting details are in the definition of fib itself. The function fib is defined as a yielder (my term). It creates a recursive helper routine fib-loop and calls it with arguments 0 and 1. That helper routine yields the current value of its first argument i, then calls itself with argument i replaced by j and j replaced with i + j.

The second part of the example loops 10 times printing the next value from fib each time around the loop.

Of course this presupposes a few features that PScheme doesn't appear to have. The while macro was already introduced in Section 9.2.2, but here it is again just for completeness:

(define while
  (macro (test body)
    '(letrec
      ((loop
         (lambda ()
           (if ,test
             (begin
               ,body
               (loop))
             ()))))
      (loop))))
[download]

You can see that it's a recursive definition, but by now that shouldn't worry you: as each call to loop is in tail position we won't grow any context or eat any stack with this definition.

The other two features we don't have yet are yield and yielder. yield is actually quite easy to write. When we say (yield value), what we really want to do is return not only the value, but also the current continuation so that the next time we are called that continuation can be called instead, returning us to where we left off. We can return more than one value by wrapping the values in a list, so notionally (yield value) means:

(^return (list current-continuation value))
[download]

where ^return is another continuation set up by the caller of the function.

Now we need a way of getting the current continuation and the only way to do that is with call/cc so, still notionally, but getting closer, (yield value) means:

(call/cc
  (lambda (current-continuation)
    (^return (list current-continuation value))))
[download]

In fact that's it, all we need to do is wrap that up in a macro, and we have yield:

(define yield
  (macro (value)
    '(call/cc
      (lambda (^here)
        (^return (list ^here ,value))))))
[download]

Next we need to look at yielder. You probably won't be surprised to find out it's another macro. It returns a function that, when called for the first time, invokes the body of the yielder expression, saving the current continuation in a ^return variable. When yield is invoked control returns through the ^return continuation. The ^here continuation part of the returned result is saved and the value part is returned by the function as a whole.

On subsequent calls, rather than invoking the body of the yielder again, the saved ^here continuation is invoked, returning control to where the yield left off. Here's yielder:

(define yielder
  (macro (body)
   '(let ((firsttime 1)
         (^resume 0)
         (^return 0))
     (lambda ()
       (if firsttime
         (let ((res (call/cc
                      (lambda (^cont)
                        (begin
                          (set! ^return ^cont)
                          ,body)))))
           (begin
               (set! firsttime 0)
               (set! ^resume (car res))
               (car (cdr res))))
         (let ((res (call/cc
                      (lambda (^cont)
                        (begin
                          (set! ^return ^cont)
                          (^resume))))))
           (begin
               (set! ^resume (car res))
               (car (cdr res)))))))))
[download]

Again, continuations are flagged with a caret.

That really is all there is to it. If this seems like a solution looking for a problem, then let me point out a very real problem for which this would be the perfect solution. Consider the venerable File::Find package from the core Perl distribution. This package allows you to specify criteria for recursively locating files in a filesystem, along with a callback subroutine which is called on each file so located. Sometimes this is exactly what you need, but sometimes you would prefer File::Find to behave as an iterator, returning the next file found on each call. With proper support for co-routines in perl, the callback function that you provide to File::Find need only yield the file to achieve exactly that, without changing a single line of the File::Find package itself!

Tests for this yield feature, which just duplicate the above code, are in Listing 27.

Listing 27. t/CPS_Yield.t

  1 use strict;
  2 use warnings;
  3 use Test::More;
  4 use lib 't/lib';
  5 use PScm::Test tests => 2;
  6 
  7 BEGIN { use_ok('PScm') }
  8 
  9 eval_ok(<<EOF, <<EOR, 'yield');
 10 (define yield
 11   (macro (value)
 12     '(call/cc
 13       (lambda (^here)
 14         (^return (list ^here ,value))))))
 15 
 16 (define yielder
 17   (macro (body)
 18    '(let ((firsttime 1)
 19          (^resume 0)
 20          (^return 0))
 21      (lambda ()
 22        (if firsttime
 23          (let ((res (call/cc
 24                       (lambda (^cont)
 25                         (begin
 26                           (set! ^return ^cont)
 27                           ,body)))))
 28            (begin
 29                (set! firsttime 0)
 30                (set! ^resume (car res))
 31                (car (cdr res))))
 32          (let ((res (call/cc
 33                       (lambda (^cont)
 34                         (begin
 35                           (set! ^return ^cont)
 36                           (^resume))))))
 37            (begin
 38                (set! ^resume (car res))
 39                (car (cdr res)))))))))
 40 
 41 (define while
 42   (macro (test body)
 43     '(letrec
 44       ((loop
 45          (lambda ()
 46            (if ,test
 47              (begin
 48                ,body
 49                (loop))
 50              ()))))
 51       (loop))))
 52 
 53 (define fib
 54   (yielder
 55     (letrec ((fib-loop
 56                (lambda (i j)
 57                  (begin
 58                    (yield i)
 59                    (fib-loop j (+ i j))))))
 60       (fib-loop 0 1))))
 61 
 62 (let ((n 10))
 63   (while n
 64     (begin
 65       (set! n (- n 1))
 66       (print (fib)))))
 67 EOF
 68 yield
 69 yielder
 70 while
 71 fib
 72 0
 73 1
 74 1
 75 2
 76 3
 77 5
 78 8
 79 13
 80 21
 81 34
 82 ()
 83 EOR
 84 
 85 # vim: ft=perl

³²

R⁶RS requires that tail calls consume no resources, not necessarily that they perform precisely the TCO demonstrated here. For now if you can just accept that implicit TCO or an equivalent is a desirable thing, all will become clear later.

³³

For an alternative exposition of TCO (sometimes called Tail Call Elimination) see [hop pp229–234]

³⁴

Actually, if we were implementing in rabid, pure CPS, then even the primitives such as multiplication would take a continuation. We could simulate that here by re-writing our continuation as:

sub { times($n, shift, $cont) }
[download]

where times() is

sub times {
    my ($x, $y, $cont) = @_;
    $cont->($x * $y);
}
[download]

which at least emphasizes that the continuation is still being passed, though it is overkill for our purposes.

³⁵

It's obvious really: Since no CPS function ever returns, any deferred computation must have been moved into the continuation, and a function call without deferred computation is by definition in tail position.

³⁶

Actually, we're also relying on the fact that perl implicitly returns the value of a tail call as the value of a function.

³⁷

The trampoline further requires that all intermediate calls also be in tail position, and that the values of all tail calls are returned, so that a returned value would be guaranteed to reach the trampoline. Fortunately, CPS satisfies the first of these requirements, and Perl satisfies the second.

³⁸

This is what is meant by “Stackless Python”: an implementation of that language in CPS with complete TCO.

³⁹

Thanks to Tom Christiansen for this idea.

⁴⁰

Assuming of course that the Cont() method is invoked in tail position, but we've been here before.

⁴¹

In general it is always considered better form to use @EXPORT_OK rather than @EXPORT. However it is justifiable here firstly because PScm::Continuation is part of PScheme, not a standalone library module, and secondly the only reason another class would use PScm::Continuation would be to gain access to the cont construct.

⁴²

The reasoning is that each call to Eval() within the interpreter corresponds to a value being calculated and, most importantly, returned in the PScheme language. These points of return are exactly the points that require continuations to be used instead.

If however in the later CPS rewrite of the object system from Chapter 12 we wanted to allow PScheme objects to supply some sort of to-string method, and have that called in preference to the underlying Perl as_string() method, then we would have to rewrite as_string() into CPS.

⁴³

Remember our CPS factorial() example before TCO, where the stack built up during calls to factorial() and built up further when the continuations actually triggered on factorial(0). Well the return in the PScm::Continuation::Cont() method takes care of the second of these contingencies, and returning a continuation here takes care of the first.

If you don't believe me, wait until we have rewritten the complete interpreter in CPS then enter the following definition in t/interactive:

> (define factorial
>     (lambda (x)
>         (if x
>             (* x (factorial (- x 1)))
>             1)))
[download]

Then try

> (factorial 170)
7257415615307998967396728211129263114716991681296451376543577798900561
8434017061578523507492426174595114909912378385207766660225654427530253
2890077320751090240043028005829560396661259965825710439855829425756896
6313439612262571094946806711205568880457193340212661452800000000000000
000000000000000000000000000
[download]

Perl would have complained long before it hit that many levels of recursion.

⁴⁴

The Fibonacci series starts with 0 and 1. the next number in the series is always the sum of the previous two, e.g. 0, 1, 1, 2, 3, 5, 8, 13, 21 ...

⁴⁵

Note that calling a continuation on undef is not the same as returning undef, the trampoline will never see this undef and terminate the computation prematurely.

Chapter 13. Continuations

13.1. Tail Recursion and Tail Call Optimization

13.2. Continuation Passing Style

13.3. Example CPS Transformations

13.4. The Trampoline

13.5. Using CPS

13.6. Implementation

13.6.1. Our Trampoline Implementation

13.6.2. CPS `let` and `lambda`

13.6.3. CPS `letrec`

13.6.4. CPS `let*`

13.6.5. CPS List Processing

13.6.6. CPS `macro` and `unquote`

13.6.7. CPS Sequences and Assignment

13.6.8. CPS `define`

13.6.9. CPS OOP

13.7. CPS Without Closures

13.8. CPS Fun

13.8.1. An `error` Handler

13.8.2. `yield`

13.9. Summary

Chapter 13. Continuations

13.1. Tail Recursion and Tail Call Optimization

13.2. Continuation Passing Style

13.3. Example CPS Transformations

13.4. The Trampoline

13.5. Using CPS

13.6. Implementation

13.6.1. Our Trampoline Implementation

13.6.2. CPS let and lambda

13.6.3. CPS letrec

13.6.4. CPS let*

13.6.5. CPS List Processing

13.6.6. CPS macro and unquote

13.6.7. CPS Sequences and Assignment

13.6.8. CPS define

13.6.9. CPS OOP

13.7. CPS Without Closures

13.8. CPS Fun

13.8.1. An error Handler

13.8.2. yield

13.9. Summary

13.6.2. CPS `let` and `lambda`

13.6.3. CPS `letrec`

13.6.4. CPS `let*`

13.6.6. CPS `macro` and `unquote`

13.6.8. CPS `define`

13.8.1. An `error` Handler

13.8.2. `yield`