What are continuations? Why should you want to know about them? The rest of this chapter is devoted to answering the first of those questions, but the second question deserves an answer early on, if only to encourage you to pursue the answer to the first question.
I hope you can remember (I certainly do) that wonderful eureka moment when you first “got” recursion, and all its implications. Grasping the concept of continuations is an even more rewarding and dare I say transcendental experience, and well worth the effort.
Continuations are an advanced control-flow technique that can be used to implement any and all standard control-flow mechanisms including but not limited to conditional branching, loops (with break statements), goto, return etc. Beyond the standard control-flow mechanisms, continuations also promise an almost limitless potential for new types of control flow that might be difficult or near impossible to achieve in any other way, for example
Let's talk a bit about co-routines.
Co-routines are groups of two or more functions or methods that interact
with one another in a much more even-handed way than just “A()
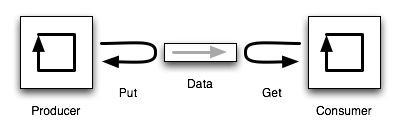
calls B().” A classic example is a producer-consumer
pair of routines, which pass data, possibly via some intermediate structure
such as a list. The producer produces data, pushing it on to the list, and the consumer consumes
it, shifting it off the list again, something like Figure 26.

Think of the producer using some complex algorithm to generate a stream of data while the consumer uses an equally complex algorithm to parse it. Both the producer and consumer are independant loops, so on the face of it, if the producer was called it would never relinquish control to give the consumer a look-in, it would just continue to push data onto that list. Likewise the consumer, if it were running, would just consume data until the list was exhausted. Both loops could have extensive internal logic and state that would make it impossible for the producer to simply call the consumer when it had produced something, because the consumer might have difficulty returning control to the producer without loosing all of its internal state. The only apparent solution would be to implement the producer and the consumer as separate threads, or even as completely separate processes and have some IPC mechanism to pass the data between them. But this pair of co-routines might only be part of a much larger system and the division into separate threads or processes might be inelegant or inappropriate. Continuations provide a solution by allowing a sort of “procedural goto” wherby control passes directly from the center of one routine to the heart of the other, and then back again, resuming exactly where the “goto” left off!
Threads are a common enough concept nowadays, but you might be surprised to hear that continuations make it almost trivial to implement so called “green” threads (application as opposed to operating system threads). We'll actually do this in a later chapter.
Exceptions are a simple application of continuations, where
control, rather than unwinding down a stack, proceeds immediately
to some handler routine. Perl's eval{die} construct is
an example of this sort of thing. We'll demonstrate a very simple
error construct towards the end of this chapter.
Logic Programming, as demonstrated by languages such as Prolog, is a completely different paradigm; it has more in common with recursive database search and large-scale pattern matching than the procedural and OO style of programming presented by PScheme. However continuations make it possible to implement the basis of such a language, and we will attempt that later on too.
I hope I have whet your appetite for the potential of continuations, however the topic of continuations is somewhat difficult, and this chapter is a long one.
Before diving in, it would be a good idea to discuss a couple of related topics, namely tail recursion and tail call optimization. Then with those under our belts, we can progress to continuations themselves. We will talk about continuations by discussing continuation passing style, a programming technique available to many languages, including Perl. Then we proceed to re-write the interpreter from Chapter 12 in continuation passing style, and by exposing the underlying continuations in the PScheme language, we show what an incredibly powerful tool they are.
Much of the above may not make much sense on first reading, but hopefully the rest of the chapter will make it clear, so let's get started.
Consider the following definition of factorial() in Perl:
sub factorial {
my ($n) = @_;
if ($n == 0) {
return 1;
} else {
return $n * factorial($n - 1);
}
}
print factorial(5), "\n"; # prints 120
This is the classic recursive definition of the factorial function: the factorial of 0 is 1, and the factorial of any other number is that number times the factorial of one less than that number.
The evolution on the stack of the call to factorial(5)
would proceed as follows:
factorial(5) 5 * factorial(4) 5 * 4 * factorial(3) 5 * 4 * 3 * factorial(2) 5 * 4 * 3 * 2 * factorial(1) 5 * 4 * 3 * 2 * 1 * factorial(0) 5 * 4 * 3 * 2 * 1 * 1 5 * 4 * 3 * 2 * 1 5 * 4 * 3 * 2 5 * 4 * 6 5 * 24 120
It is obvious that the stack grows (to the right in the example)
and that there are deferred multiplications that only get performed
as the calls to factorial() return and the stack is
unwound again.
We can rewrite that factorial function in a different form with the addition of a helper function, like so:
sub factorial {
my ($n) = @_;
return factorial_helper($n, 1);
}
sub factorial_helper {
my ($n, $result) = @_;
if ($n == 0) {
return $result;
} else {
return factorial_helper($n - 1, $n * $result);
}
}
print factorial(5), "\n"; # still prints 120
This is still a recursive definition, but it differs from the
original in one crucial detail: the last thing
factorial_helper() does is to call itself recursively
and it immediately returns the result. In the original
definition the result of the recursive call to factorial()
had to be multiplied by the current value of $n before it
could be returned.
A function which is called and its value immediately returned
is said to be in tail position and the code making the
call is said to be making a tail call. A recursive
function which calls itself in tail position is said to be
tail recursive. Tail calls are special because the stack
setup to make the call and teardown afterwards is essentially
redundant: the value of the function making the tail call is the
value of the function being called, and
the caller's stack frame is destroyed immediatly after
the called function's stack frame is. If we could overwrite the
caller's arguments with the arguments to the called function, then
goto the called function, then when that function does a
return
it will return not to the caller, but to the caller of the caller.
This is called tail-call optimization (TCO).
Figure 27 shows a normal procedure call in tail postion. You can see that the environment is extended by the called function's frame, then that extension is discarded as the called function returns, then the calling function's frame is subsequently discarded as the calling function returns to the previous caller (we are talking about the Perl stack here, not PScheme environments).
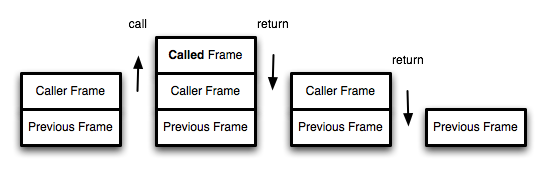
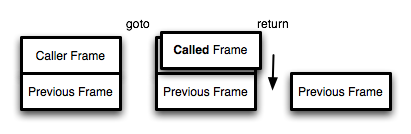
Figure 28 shows the effect of tail call optimization. The caller's frame is replaced by the called function's frame, then the caller jumps to the called function. When the called function returns it does so directly to the previous caller.
Perl allows us to do precisely this, by means of assignment to
@_ and the special goto &sub syntax. Here's
our factorial_helper() again, this time with TCO:
sub factorial_helper {
my ($n, $result) = @_;
if ($n == 0) {
return $result;
} else {
@_ = ($n - 1, $n * $result);
goto \&factorial_helper;
}
}
This function, although written in a recursive style, operates in a constant space and consumes no stack.
Many language implementations (gcc springs to
mind) can perform implicit TCO, detecting
calls in tail position and replacing the call with
a goto, and that's all calls
in tail position, not just recursive ones.
Furthermore, some languages such as Scheme require this
behaviour of their implementations29.
Our PScheme implementation, through the use of continuations, will by the end of this chapter support something equivalent.
That's really all there is to tail recursion and TCO. I've already said they have a direct bearing on continuations, but there is a lot more to continuations than that, so lets take a look at using continuations in perl.
This section discusses continuation passing style (CPS). It contains a number of exclaimation marks; I hope you will agree that they are justified.
One way of thinking about a procedural computation is by decomposing it into just two main operations:
Continuation passing style eliminates the second of these operations; in pure continuation passing style no function you call ever returns!
...That being the case, you need to figure out how to tell a CPS function what to do with its result. So, since a CPS function can't return a value, it is instead passed an additional procedure as argument: a continuation, and calls the continuation on the result.
The continuation represents the remainder of the computation
after a function “returns”. Since calling a continuation is
equivalent to returning a value in non-CPS, you can also think
of a continuation as a reference to your function's return
statement.
As you might imagine, a computation which never returns will simply consume stack indefinately, until it completes, but I hope the discussion of TCO above has addressed some of your reservations on that score, and as I've said, continuations themselves, when fully realised, provide an alternative mechanism for dealing with the same issue.
So what does continuation passing style look like in Perl? Well
since continuations are procedures, closures are an obvious
and easy way to implement them.
So our continuations will be created by
sub { ... }
and called by $continuation->(...).
For a first example of CPS transformation,
we'll go back to our original factorial()
function from Section 13.1 and re-write
it in CPS. To save you having to refer back to it, here
it is again.
sub factorial {
my ($n) = @_;
if ($n == 0) {
return 1;
} else {
return $n * factorial($n - 1);
}
}
print factorial(5), "\n"; # prints 120
Now as we have said, all CPS functions take an additional continuation argument. The continuation we pass it depends on what we want to do with the result. Our original example printed the result, so let's just pass a continuation to do that:
factorial(5, sub { print shift, "\n" });
The additional continuation argument sub { print shift "\n" }
just takes one argument and prints it.
Now let's re-implement factorial() itself in CPS. It takes
an additional continuation as argument, so the first couple of lines
are easy:
sub factorial {
my ($n, $ret) = @_;
Next remember that whenever the function used to return a value,
it must now call its continuation on that value, so the
next couple of lines are also pretty easy: wheras the original
returned 1 if $n was 0, the CPS version
calls its continuation on the value 1 instead.
if ($n == 0) {
$ret->(1);
This works for factorial(0, sub { print shift, "\n" } ):
the continuation will get and print a 1.
That leaves the tricky bit. The original function reads:
} else {
return $n * factorial($n - 1);
If you get stuck on a difficult CPS transform, it always pays to break the expression in question into a sequence of simpler operations first. We can do that here easily enough:
} else {
my $factorial_result = factorial($n - 1);
my $result = $n * $factorial_result;
return $result;
So this is much easier now. You can see that the first thing that
happens is that factorial() calls itself. Now we know that the
call to factorial() will never return, so
we have to pass factorial() a continuation that will perform
the computation that would have occurred after that call to
factorial() returned in the original.
Note also that where the original function did a return $result,
our new continuation must call the original continuation on the
$result instead.
} else {
factorial($n - 1, sub {
my ($factorial_result) = @_;
my $result = $n * $factorial_result;
$ret->($result);
}
);
Now we can shorten the above continuation by eliminating the temporary variables:
} else {
factorial($n - 1, sub { $ret->($n * shift) });
The new continuation is sub { $ret->($n * shift) }.
It takes one argument: the result so far (this is the value that
our non-CPS factorial() would have returned). It multiplies
the result by the current value of $n then calls the current
continuation $ret on that value30.
That completes our initial CPS implementation of factorial():
sub factorial {
my ($n, $ret) = @_;
if ($n == 0) {
$ret->(1);
} else {
factorial($n - 1, sub { $ret->($n * shift) });
}
}
factorial(5, sub { print shift, "\n" }); # still prints 120
At the risk of labouring the point, consider the call:
factorial(3, sub { print shift, "\n" });
The evolution of the continuation will proceed as follows:
sub {
print shift, "\n"
}
sub {
sub {
print shift, "\n"
}->(3 * shift)
}
sub {
sub {
sub {
print shift, "\n"
}->(3 * shift)
}->(2 * shift)
}
sub {
sub {
sub {
sub {
print shift, "\n"
}->(3 * shift)
}->(2 * shift)
}->(1 * shift)
}
sub {
sub {
sub {
sub {
print shift, "\n"
}->(3 * shift)
}->(2 * shift)
}->(1 * shift)
}->(1) # factorial 0
sub {
sub {
sub {
print shift, "\n"
}->(3 * shift)
}->(2 * shift)
}->(1)
sub {
sub {
print shift, "\n"
}->(3 * shift)
}->(2)
sub {
print shift, "\n"
}->(6)
print 6, "\n"
The deferred multiplications accumulate until we reach the
point where the entire accumulated continuation is finally called
with argument 1,
then they unwind from the outside in until the original continuation
gets invoked on the argument 6 and 6 is printed.
Still sticking with our CPS factorial(),
there is more that we can do.
Because in CPS no function ever returns, all function
calls must be in tail position31.
As you can see our recursive call to factorial() is now
in tail position, so we can use TCO to remove
the spurious use of stack:
sub factorial {
my ($n, $ret) = @_;
if ($n == 0) {
$ret->(1);
} else {
@_ = ($n - 1, sub { $ret->($n * shift) });
goto \&factorial;
}
}
This is still a “recursive” definition of factorial(),
but now it is not the stack which is growing, but the continuation
itself which consumes more and more space as our computation
proceeds.
An astute reader will have realised that, in fact, we are still
using stack when the continuations actually get triggered: those
calls to $ret->($n * shift) will of course use just as
much stack as the original did. However note that the continuations
themselves are called in tail position, so with a little more work
we can eliminate that stack overhead too:
sub factorial {
my ($n, $ret) = @_;
if ($n == 0) {
@_ = (1);
goto $ret;
} else {
@_ = ($n - 1, sub { @_ = ($n * shift); goto $ret; });
goto \&factorial;
}
}
This is very messy, but it works as advertised. Just bear in
mind that in a language that provided implicit TCO,
we wouldn't need any of those assignments to @_ or the
gotos, and I've promised that continuations themselves
will allow an alternative and cleaner solution in our interpreter.
Moving on, what about that iterative/recursive definition of
factorial() with a helper function
from Section 13.1? We can
re-write that in CPS too. How does it compare? Well first here's a
non-CPS variation on the
original again, thoroughly TCO'd this time:
sub factorial {
my ($n) = @_;
@_ = ($n, 1);
goto \&factorial_helper;
}
sub factorial_helper {
my ($n, $result) = @_;
if ($n == 0) {
return ($result);
} else {
@_ = ($n - 1, $n * $result);
goto \&factorial_helper;
}
}
print factorial(5), "\n"; # prints 120
and here it is re-written in CPS:
sub factorial {
my ($n, $ret) = @_;
@_ = ($n, 1, $ret);
goto \&factorial_helper;
}
sub factorial_helper {
my ($n, $result, $ret) = @_;
if ($n == 0) {
@_ = ($result);
goto $ret;
} else {
@_ = ($n - 1, $n * $result, $ret);
goto \&factorial_helper;
}
}
factorial(5, sub { print shift, "\n" }); # still prints 120
Our new tail recursive CPS factorial() function takes an
additional continuation argument and passes that to
factorial_helper(). factorial_helper() either goes to
the continuation with the result, or goes to itself with new values
for $n and $result; but since it has no deferred
computation, it does not need to construct a new continuation and
just passes the existing continuation to the recursive call.
The take home message here is that the tail recursive definition of
factorial() translates into a CPS where neither the stack
nor the continuation grows. This is a general result: functions written
to be tail-recursive consume no stack when TCO'd, and do not
build new continuations when rewritten into CPS.
The “normal” way, or at least the easiest way to produce CPS code is to do what we did above: take non-CPS code and translate it into CPS. In the next section we're going to look at a few examples of simple, hypothetical function forms and how they translate into CPS.
To keep these examples simple, we'll ignore any issues of TCO. These examples should allow us to proceed with more confidence into the subsequent rewrite of our interpreter.
The simplest kind of function is one that takes no arguments and returns a constant:
sub A {
return 'hello';
}
The CPS form of this takes a continuation as argument and calls the continuation on the constant:
sub A {
my ($ret) = @_;
$ret->('hello');
}
I've called the continuation $ret to emphasize it's
similarity to a return statement.
One of the guiding principles of converting to CPS is
that calling the argument continuation in CPS is equivalent to doing
a return in non-CPS. In fact you can mentally substitute
return(...) for $ret->(...) in many of
these examples without disturbing the sense of them.
The next simplest form is a function that takes arguments and performs only primitive operations such as addition on them, returning the result:
sub A {
my ($x, $y) = @_;
return $x + $y;
}
In this case, since primitive operations can't take a continuation, and because they are “terminal” operations that won't run away off up the stack, we again can just call the continuation on the result:
sub A {
my ($x, $y, $ret) = @_;
$ret->($x + $y);
}
Next come simple functions that just call another function without any deferred computation:
sub A {
my ($x) = @_;
return B($x);
}
Here, since there is no deferred computation, there need be no new continuation, we just pass the existing continuation to the called function:
sub A {
my ($x, $ret) = @_;
B($x, $ret);
}
This is just saying to B() “return your result here.”
Now we're starting to get into areas where there is deferred computation, and this is where it starts to get just a little bit tricky:
sub A {
return C(B());
}
B() gets called first, and
the value it returns is passed as argument to C().
In CPS B() would never return so we must also call it first,
passing it a
new continuation that calls C() with B()'s result
and the current continuation:
sub A {
my ($ret) = @_;
B(
sub {
my ($B_result) = @_;
C($B_result, $ret);
}
);
}
The new continuation calls C() with two arguments:
the result of the call to B(), and the original continuation
$ret to which C() should return its result.
Since the original call to C() was returned as the result of
the call to A(), C() is being told “return
your result here”.
Sequential function calls present a slightly different problem.
sub A {
B();
C();
D();
}
Here we must construct a nest of continuations to ensure that
C() and D() get called in the correct order after B():
sub A {
my ($ret) = @_;
B(
sub {
C(
sub{
D($ret);
}
);
}
);
}
We call B() with a continuation that will call C()
with a continuation that will call D() with the original
continuation $ret since the result of the call to D()
was the result of the original call to A(). Again this is just saying
to D() “return your result here.”
Next let's look at a conditional expression:
sub A {
my ($x) = @_;
if (B($x)) {
return C($x);
} else {
return D($x);
}
}
The call to B() in the condition will never return,
so we must pass it a continuation that tests its result and decides
which branch to take accordingly, passing the the original continuation
to the chosen branch:
sub A {
my ($x, $ret) = @_;
B($x,
sub {
my ($B_result) = @_;
if ($B_result) {
C($x, $ret);
} else {
D($x, $ret);
}
}
);
}
Both the true and the false branch used to make a single call
in tail position to C() or D(), so now we simply pass
the original continuation unchanged as an additional argument
to C() or D().
Finally, for now, lets look at a looping function.
sub A {
my $i = 0;
while ($i < 10) {
B();
++$i;
}
}
This needs a bit more thought. It turns out to be easiest to do a preliminary rewrite of this example into a recursive form as follows:
sub A {
A_h(0);
}
sub A_h {
my ($i) = @_;
if ($i < 10) {
B();
A_h($i + 1);
}
}
Turning that into CPS then becomes just a re-application of examples we've seen before:
sub A {
my ($cont) = @_;
A_h(0, $cont);
}
sub A_h {
my ($i, $cont) = @_;
if ($i < 10) {
B(
sub { A_h($i + 1, $cont); }
);
}
}
The examples above hopefully give a taste of the sorts of
transformations that we shall be applying to our interpreter soon.
There are other more difficult cases that might appear impossible
at first sight (uses of map for example,) but again they can be
resolved by first re-writing the expressions in a more tractable
form before converting to CPS. We'll see examples of this sort
of thing when we get to them.
It happens that there does exist a formal methodology for transforming statements in any language capable of supporting CPS into CPS. The above example transformations are samples from that ruleset. All such transformations can be automated. When I started this chapter I was hopeful that perhaps something in the B package, the Perl compiler, would be available that could perform the transform but that appears not to be the case. Anyhow we'll learn a lot more about CPS by performing the transform manually, so that is the best approach to take.
I promised that there was an alternative
to all the messy assignments to @_ and the gotos that
constitute TCO.
Well that falls out of three related properties of a
fully realised CPS:
Now just suppose that at well chosen points we do return something, and not just anything. Suppose we return another continuation, this time taking no arguments, that when called just continues the calculation from where it left off!
You may need to convince yourself that this will work: Since we can TCO a CPS function, such that it uses no Perl stack at all, then even if the CPS code is not TCO'd there can be nothing on the Perl stack that it actually needs, just a long chain of return adresses that it pases through after the computation is finished. That is one of the surprising things about continuations, that they are completely self-contained and require no external context to operate.
So how do we deal with this returned continuation?
A handler routine, called a trampoline, starts off
by being called with a continuation of no arguments. It loops,
repeatedly calling the continuation and assigning the result (another
continuation of no arguments) back to the continuation itself
until the result is undef. The code is easier to write
than to describe:
sub trampoline {
my ($cont) = @_;
$cont = $cont->() while defined $cont;
}
To give you a feel of how this might work, let's return once
more to our CPS factorial() function and re-write it
to make use of a trampoline instead of TCO. First to
refresh your memory here's our first CPS attempt
again (slightly modified) before we TCO'd it:
sub factorial {
my ($n, $ret) = @_;
if ($n == 0) {
$ret->(1);
} else {
factorial($n - 1,
sub {
my ($a) = @_;
$ret->($n * $a)
});
}
}
factorial(5, sub { print shift, "\n"; }); # still prints 120
and here it is rewritten to use a trampoline.
sub factorial {
my ($n, $ret) = @_;
if ($n == 0) {
return sub { $ret->(1); };
} else {
return sub {
factorial($n - 1,
sub {
my ($a) = @_;
return sub { $ret->($n * $a) }
});
};
}
}
sub trampoline {
my ($cont) = @_;
$cont = $cont->() while defined $cont;
}
trampoline(
sub {
factorial(5, sub { print shift, "\n"; return undef; });
}
); # still prints 120
Changes from the original are in bold as usual. The key to
understanding this is to notice that whenever a function call was
done in the original, either to factorial() or to the
continuation, a closure which will make that call is returned to
the trampoline instead. Each time this happens the stack is completely
cleared down and the trampoline resumes the computation by calling the
returned closure.
Finally, at the end of the computation, the original continuation passed to factorial()
gets invoked, printing the result and returning undef to
the trampoline causing it to stop.
Like TCO, the trampoline technique is not specific to CPS, but both techniques require that the modified calls be in tail position, making CPS a prime candidate for either kind of optimisation33.
Well that's pretty scary stuff. Both TCO and the trampoline are simply alternative strategies to avoid unlimited use of the stack, and you may be wondering if the trampoline has any advantages over TCO at this point. I'd like to make a few arguments in favour of the trampoline here.
factorial() example is a very tight piece of code which
somewhat overemphasizes the role of the trampoline by doing a lot
with it in a small space. Particularily the explicit return of a
closure to make the recursive call does not have to be done for
every tail call, we just need to ensure it happens fairly
regularily on our way up the stack. For example in a set of mutually
tail recursive subroutines, A() calling B() calling
C() calling A()..., only one of those subroutines
need do that return. This is in contrast to TCO, where any
unoptimised tail call constitutes a permanently unclaimed stack
frame. return
to the trampoline in the method that invokes the closure (provided
that method is invoked in tail position).
It is the third argument that swings the case, and that's exactly what we'll be doing. If you don't get that argument yet, hold on and it will be made clear later.
Thinking back to our original exposition of CPS from Section 13.2 where we suggested that normal procedural programming consisted primarily of calling functions and returning values, we said that CPS eliminates the second of these two operations. In fact that was a slight oversimplification. There is a certain amount of equivalence between the operations of “call” and “return”, it is just the direction of the flow of data that differs, “upwards” to the called function via its arguments, versus “downwards” from the called function via its return value. Continuation passing style in fact unifies these two operations, returning a value is the same as calling a function. Since in CPS data flows in only one direction, in some sense CPS is actually a simplification!
Furthermore, an application written in CPS with complete TCO needs no stack at all: TCO allows us to eliminate the use of stack by tail calls, and in CPS all function calls are tail calls34.
So now you understand continuations, but how do you use them?
Well at each step of a computation you have a continuation representing
the current function's return statement. But a continuation
is a variable, a reference to a subroutine, and you can do
whatever you like with it!. You don't have to call
it (return through it) just when everyone is expecting you to, you
might call (return through) a completely different continuation
instead, or you might pass it to another function that can call it
(return through it) if it likes. And when a continuation is called
(returned through), control flow transfers to wherever the
return statement equivalent to that continuation would
have returned! Put another way, you have always had control over
what value your function returns, and when it returns it, but not
until now have you had control over where it returns it to!
And there's more. Although code written in CPS retains the notion of a stack since functions call functions and return values (via continuations); as we've already noted the stack is not really relevant, or even necessarily present. Any continuation is as valid as any other. It is perfectly permissable to call a continuation that resumes control in a function that has already returned, in effect jumping across the call graph that a stack based language is constrained by!
Let's give an explicit example to illustrate this last point. Consider the following simple perl script:
sub A {
print "in A\n";
B();
print "back in A\n";
}
sub B {
print " in B\n";
C();
print " back in B\n";
}
sub C {
print " in C\n";
}
sub X {
print "in X\n";
Y();
print "back in X\n";
}
sub Y {
print " in Y\n";
Z();
print " back in Y\n";
}
sub Z {
print " in Z\n";
}
A();
X();
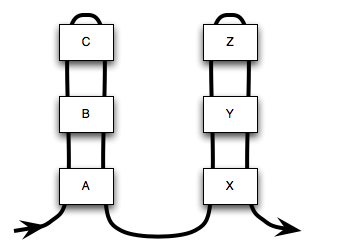
A() calls B() which calls C(), and
X() calls Y() which calls Z(). The top level
calls A() then X(). You shouldn't take too long
to convince yourself that it will produce the following output:
in A
in B
in C
back in B
back in A
in X
in Y
in Z
back in Y
back in X
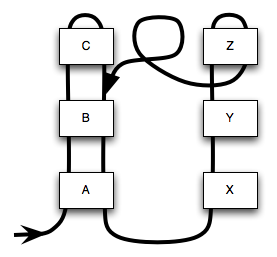
Just to hammer home the simple point, Figure 29
shows the thread of control flow passing through
A(), B(), C(), X(), Y() and Z().
Now let's re-write that program into CPS, without changing any of it's behaviour:
sub A {
my ($ret) = @_;
print "in A\n";
B(sub { $ret->(print "back in A\n") });
}
sub B {
my ($ret) = @_;
print " in B\n";
C(sub { $ret->(print " back in B\n") });
}
sub C {
my ($ret) = @_;
$ret->(print " in C\n");
}
sub X {
my ($ret) = @_;
print "in X\n";
Y(sub { $ret->(print "back in X\n") });
}
sub Y {
my ($ret) = @_;
print " in Y\n";
Z(sub { $ret->(print " back in Y\n") });
}
sub Z {
my ($ret) = @_;
$ret->(print " in Z\n");
}
A(sub { X(sub {})});
There are no new tricks that haven't already been described in Section 13.3 above, the only difference is that since none of the original functions actually returned anything interesting (they returned the results of print statements), the equivalent continuations don't bother looking at their arguments.
This produces identical output to the original program, and exhibits exactly the same control flow. Now let's make just three tiny changes.
my $cont;
sub A {
my ($ret) = @_;
print "in A\n";
B(sub { $ret->(print "back in A\n") });
}
sub B {
my ($ret) = @_;
print " in B\n";
C(sub { $ret->(print " back in B\n") });
}
sub C {
my ($ret) = @_;
$cont = $ret;
$ret->(print " in C\n");
}
sub X {
my ($ret) = @_;
print "in X\n";
Y(sub { $ret->(print "back in X\n") });
}
sub Y {
my ($ret) = @_;
print " in Y\n";
Z( sub { $ret->(print " back in Y\n") });
}
sub Z {
my ($ret) = @_;
$cont->(print " in Z\n");
}
A(sub { X(sub {})});
The first change is to declare a $cont variable to
hold a continuation. Then C(), before it calls its continuation,
stores it in this $cont variable. Finally Z(), instead
of calling its own continuation $ret, calls the saved
continuation $cont instead.
This produces the output below. Whether or not you find this surprising will depend on how closely you've been following the discussion:
in A
in B
in C
back in B
back in A
in X
in Y
in Z
back in B
back in A
in X
in Y
in Z
back in B
back in A
in X
in Y
in Z
back in B
back in A
...
All proceeds normally until we reach the first call to Z().
Since Z() calls the continuation that C() saved, Z()
instead of returning to X(), returns to B() instead.
Then normal service is resumed, starting from the return to
B(), until the next return from
Z(), which again returns to B() and so on,
ad infinitum.
what we have achieved is the control flow shown in
Figure 30.
(Cue the Mony Python music.) You can probably imagine at this stage that with a little more work on this example, adding loops and passing continuations around, we could easily arrive at a coroutine implementation, where control does jump from the heart of one loop to the heart of another and back again without disturbing the state of either loop.
There is a big downside to writing in CPS however, and that
is that it makes your head hurt. A far better approach is to use a
language that has continuations built in “under the hood”.
Then when you write “return $val” you are really calling
a continuation on $val, but you don't have to worry
about it, and when you need to get hold of a continuation, you can
ask for one. A language like that provides continuations as first
class objects in that they can be passed around as variables,
much in the same way as Perl provides anonymous subroutines
(closures) as first class objects.
For example, if Perl had built-in continuations, and we could get at
the current continuation by i.e. taking a reference to the return
keyword35, then we could rewrite all of this example
without CPS, as follows:
my $cont;
sub A {
print "in A\n";
B();
print "back in A\n";
}
sub B {
print " in B\n";
C();
print " back in B\n";
}
sub C {
$cont = \return;
print " in C\n";
}
sub X {
print "in X\n";
Y();
print "back in X\n";
}
sub Y {
print " in Y\n";
Z();
print " back in Y\n";
}
sub Z {
print " in Z\n";
$cont->()
}
A();
X();
Bold text shows the differences from the original non-CPS version.
We are going to turn our PScheme interpreter into just such a language. The next few sections will describe the changes we need to make.
Rather than attempting to rewrite the interpreter of Chapter 12 from start to finish in CPS, We're going to backtrack
to our first “interesting” interpreter, from Chapter 5
which has only let and lambda, and re-implement that. This
has the advantage that we get a real working interpreter with
continuations which we can test early on, and we can demonstrate
some of the power of continuations with it. Then I'll gloss the
re-writing of the final interpreter in stages by working through
the intermediate versions pausing only to study any previously
unencountered constructs that require novel treatment. Finally we'll
have a continuation-passing version of the interpreter from Chapter 12 to play with.
Our implementation of the trampoline does not differ significantly
from the example that we presented for factorial() above.
But it is still best introduced gradually, so this section is
still pseudocode, to a certain extent.
Firstly we need to rewrite the read-eval-print loop into CPS, so that we can call the whole thing from the trampoline. This isn't actually very difficult to do, the repl for version 0.0.2 conceptually is as simple as
sub repl {
my ($reader, $outfh) = @_;
while (my $expr = $reader->read()) {
my $result = $expr->Eval(new env);
$result->Print($outfh);
}
}
We've already seen in Section 13.3 that the easiest way
to transform a while loop into CPS is first to rewrite it
into a recursive form, and this is easy to do here:
sub repl {
my ($reader, $outfh) = @_;
if (my $expr = $reader->read()) {
my $result = $expr->Eval(new env);
$result->Print($outfh);
repl($reader, $outfh);
}
}
Now to recast that into CPS is fairly trivial, especially
if we remember that the reader PScm::Read::Read() already
returns undef on EOF, and it can continue to do so,
telling the trampoline to stop, and only calling its continuation
if there is something to evaluate.
sub repl {
my ($reader, $outfh, $ret) = @_;
$reader->read(
sub {
my ($expr) = @_;
$expr->Eval(
new env,
sub {
my ($result) = @_;
$result->Print(
$outfh,
sub { repl($reader, $outfh, $ret) }
)
}
)
}
)
}
So apart from the return of undef by
the reader,
where would we put these return statements
that return a continuation to the trampoline?
Well as I've said we could place them
throughout the code, but there's a better idea.
Instead of continuations being simple anonymous subroutines,
we make them into objects that contain those anonymous
subroutines, with a Cont() method to invoke the underlying closure.
Then instead of just writing:
$ret->($arg);
to invoke a continuation, we say:
$ret->Cont($arg);
Then, in that Cont() method, instead of just saying
sub Cont {
my ($self, $arg) = @_;
$self->{cont}->($arg);
}
we instead write
sub Cont {
my ($self, $arg) = @_;
return sub { $self->{cont}->($arg) };
}
we have both effected the return of a continuation to the trampoline, and completely hidden the fact from the client code36!
In reality there are a few minor complications with this approach, but the above discussion is very close to our final implementation.
let and lambdaIn this section we re-implement the interpreter version 0.0.2
from Chapter 5 in continuation passing style. Once that
is done, we introduce a new construct, call/cc, which
allows the language direct access to continuations.
First of all we need a new PScm::Continuation class.
I don't want to show you all of that class just yet, but here's its
new() method:
13 sub new { 14 my ($class, $cont) = @_; 15 bless { cont => $cont }, $class; 16 }
It takes an anonymous subroutine as argument and stores it in
a cont field. We don't want to be writing
new PScm::Continuation( sub {...} ) all over the place, so
we sweeten things with a little syntactic sugar:
18 sub cont(&) { 19 my ($cont) = @_; 20 return __PACKAGE__->new($cont); 21 }
This is put on PScm::Continuation's @EXPORT
list37
so after importing it with “use PScm::Continuation;”,
instead of writing new PScm::Continuation( sub {...} ) we
just write cont {...} instead.
As discussed above, we add a trampoline()
subroutine to PScm which repeatedly invokes the continuation
returned from its previous invocation, until the invocation returns
undef,
signaling the end of the computation. Here's trampoline():
70 sub trampoline { 71 my ($cont) = @_; 72 $cont = $cont->Bounce() while defined $cont; 73 }
It's functionally equivalent to the prototype
trampoline() subroutine discussed above.
The Bounce() method is defined in PScm::Continuation
to immediately invoke the continuation with no arguments:
39 sub Bounce { 40 my ($self) = @_; 41 $self->{cont}->(); 42 }
Only trampoline() calls Bounce().
Now we need to look at the Read-Eval-Print loop from PScm, with the trampoline in place.
32 sub ReadEvalPrint { 33 my ($infh, $outfh) = @_; 34 35 $outfh ||= new FileHandle(">-"); 36 my $reader = new PScm::Read($infh); 37 trampoline(cont { repl($reader, $outfh) }); 38 }
It's the same as we've seen before up to
line 37
where instead of entering it's loop,
it invokes the trampoline with a continuation.
That continuation invokes a new helper routine repl()
with the reader and the current output handle as arguments.
Here's repl().
40 sub repl { 41 my ($reader, $outfh) = @_; 42 $reader->Read( 43 cont { 44 my ($expr) = @_; 45 $expr->Eval( 46 new PScm::Env( 47 let => new PScm::SpecialForm::Let(), 48 '*' => new PScm::Primitive::Multiply(), 49 '-' => new PScm::Primitive::Subtract(), 50 if => new PScm::SpecialForm::If(), 51 lambda => new PScm::SpecialForm::Lambda(), 52 'call/cc' => 53 new PScm::SpecialForm::CallCC(), 54 ), 55 cont { 56 my ($result) = @_; 57 $result->Print( 58 $outfh, 59 cont { 60 repl($reader, $outfh); 61 } 62 ) 63 } 64 ) 65 } 66 ) 67 }
So the guts of the old ReadEvalPrint() have been moved
to repl(). It's just an expansion of the CPS pseudocode
for repl() in the previous section, and not nearly as bad as
it might first appear, it's really just Read() calling
Eval() calling Print() calling
repl(), all through passed continuations.
There is also something new added to the environment.
we'll see what that new binding call/cc on
line 53
is about later.
So the Read(), Eval() and Print() methods
now all take continuations and must be modified accordingly.
Thankfully the modifications to Read() and Print()
are trivial.
First we need to look at the CPS Print() method.
75 sub Print { 76 my ($expr, $outfh, $cont) = @_; 77 print $outfh $expr->as_string, "\n"; 78 $cont->Cont($expr); 79 }
It just does what it used to do, then calls its continuation
with an arbitrary argument. That is the continuation that will
restart the repl and it doesn't actually expect an argument, but
Cont() does so we're just playing nice.
Notice that on
line 77
we don't pass a continuation to the as_string()
method. This is just a normal non-CPS method call. The reasoning
behind that is that although as_string() is potentially recursive,
at no point will it cause evaluation of any PScheme expressions.
Since we are only interested in continuations that
might be exposed to user code, we can classify any method call that
cannot result in a call to Eval() as a simple expression
and deal with it as an atomic operation. Contrarywise, calls to
Eval() or calls to methods that might result in a call to Eval()
are classified as significant expressions, and must be
rewritten into CPS.
This distinction makes our rewrite
much simpler38.
As described above, that Cont() method actually
returns a continuation of
zero arguments which the trampoline will execute (by calling
Bounce() on it). This is the trick I was enthusing about
earlier: to return a continuation to the trampoline that will call
the current continuation, rather than just directly calling the
current continuation. The return will fall all the way
back to the trampoline, effecting a complete cleardown of whatever
stack might have accumulated up to this point, then the trampoline
will kick things off again:
34 sub Cont { 35 my ($self, $arg) = @_; 36 return cont { $self->{cont}->($arg) }; 37 }
The really neat thing about this is that the code that is written to use this method neither knows nor cares that the continuation is not simply being invoked directly at this point. The presence of the trampoline is completely invisible to the client CPS code.
Let's take a look at Read() in PScm::Read
next.
In fact what we have done is to rename Read() to _read(),
leaving it otherwise unchanged:
17 sub _read { 18 my ($self) = @_; 19 20 my $token = $self->_next_token(); 21 return undef unless defined $token; 22 23 return $token unless $token->is_open_token; 24 25 my @res = (); 26 27 while (1) { 28 $token = $self->_read; 29 die "unexpected EOF" 30 if !defined $token; 31 last if $token->is_close_token; 32 push @res, $token; 33 } 34 35 return new PScm::Expr::List(@res); 36 }
Then we provide a new Read() that handles the continuation.
63 sub Read { 64 my ($self, $cont) = @_; 65 my $res = $self->_read(); 66 return undef unless defined $res; 67 $cont->Cont($res); 68 }
Read() collects the result of the call to _read(),
and if it is undef signifying EOF
it returns undef to the trampoline telling it to stop.
Otherwise it calls its continuation on the result.
Next we need to take a look at Eval().
All Eval() methods now also take an
additional continuation as argument. All the Eval() methods are
in subclasses of PScm::Expr. Let's start by looking at
the simplest of those expressions: literals and symbols.
The old Eval() method in PScm::Expr just returned
$self (numbers, strings and anything else by
default evaluate to themselves). The new version is
little different, it calls its argument continuation on itself:
12 sub Eval { 13 my ($self, $env, $cont) = @_; 14 $cont->Cont($self); 15 }
Now for PScm::Expr::Symbol::Eval().
The old Eval() method in PScm::Expr::Symbol returned
$env->LookUp($self).
Our CPS version calls its continuation on that result instead,
because we can treat the call to LookUp() as a
simple expression:
103 sub Eval { 104 my ($self, $env, $cont) = @_; 105 $cont->Cont($env->LookUp($self)); 106 }
Evaluation of lists is a little more tricky, so to refresh
our memories here's the original PScm::Expr::List::Eval()
before CPS transformation:
62 sub Eval { 63 my ($self, $env) = @_; 64 my $op = $self->first()->Eval($env); 65 return $op->Apply($self->rest, $env); 66 }
On line 64 It
evaluates the first component of the list to get the operator
$op, then on line 65
it applies the operation $op to the rest of the unevaluated
list.
Here's the CPS form:
63 sub Eval { 64 my ($self, $env, $cont) = @_; 65 return cont { 66 $self->first()->Eval( 67 $env, 68 cont { 69 my ($op) = @_; 70 $op->Apply($self->rest, $env, $cont); 71 } 72 ); 73 }; 74 }
There's rather a lot going on here, so best we approach it in two stages.
Firstly the return cont { ... } block
wraps the entire method body in
a continuation that we return to the trampoline. Apart from
PScm::Continuation::Cont() this is the only other
place where we explicitly fall back down to the trampoline. This is because
all recursive calls to Eval() and Apply() must pass through this
single function, and so we can stop all runaway stack consumption
by Eval() and Apply() here39. You can
just ignore the return cont wrapper
and consider only the body of the continuation as if it were the
body of the function. It would still
work, but might run out of stack in the long run.
Secondly inside the method proper we assume that the first call to
Eval(), in order to to get
the $op, will
not return, so we pass it a continuation which accepts the result
$op, and applies it to the rest of the list, passing in the
original continuation
(line 70). We must
pass the original continuation $cont to Apply(), rather
than just calling the continuation on the result of the Apply(),
because the Apply() might make calls to Eval() to evaluate arguments
to the $op, among other things, and must therefore be
rewritten in CPS.
So that's it for the rewrite of all of the Eval() methods in
PScm::Expr. Now we need to
follow the chain of continuation passing into the various Apply()
methods we have. Since this is an early version of the interpreter,
there aren't too many, in fact they are in:
Starting with PScm::Primitive::Apply(), you'll remember
that all primitive operations share a common Apply() method. Now
individual primitives do not have to accept continuations
because they are terminal operations, so all that we have to do
is to call the continuation that was passed to the shared primitive
Apply() on the result of applying the individual primitive to its
arguments.
Unfortunately this is complicated by the fact that the primitive
Apply() must first evaluate its arguments. The original primitive
Apply() did it with map:
7 sub Apply { 8 my ($self, $form, $env) = @_; 9 10 my @unevaluated_args = $form->value; 11 my @evaluated_args = map { $_->Eval($env) } @unevaluated_args; 12 return $self->_apply(@evaluated_args); 13 }
This is a little tricky to rewrite in CPS, so we're going to
attack it in stages. Stage one will be to write a recursive version
of the builtin map, which instead of taking a sub and list,
takes a listref and an environment, and for each element of the
listref, calls that element's Eval() method with the environment
as argument, accumulating the result in a new listref. But wait a
minute, don't we already have such a recursive map_eval()
method? Yes, we wrote just such a method when we implemented
true list processing for version 0.0.5 back in
Section 8.5.1.
Here's that method again.
122 sub map_eval { 123 my ($self, $env) = @_; 124 return $self->Cons($self->{first}->Eval($env), 125 $self->{rest}->map_eval($env)); 126 }
Now remember that that is code from 0.0.5, and here we're
just rewriting version 0.0.2, so we don't have true list processing
yet, lots of our methods are still expecting Perl array references,
we don't have a Cons() method, and we don't have any
PScm::Expr::List::Null class. Nonetheless we can cast this
method back in to 0.0.2 terms quite easily.
This 0.0.2 map_eval() method is not yet in CPS form:
sub map_eval {
my ($self, $env) = @_;
if (@$self) {
return [ $self->first->Eval($env),
@{ $self->rest->map_eval($env) } ];
} else {
return [];
}
}
This is pretty straightforward.
The second stage of our attack is to re-write map_eval()
in CPS. It will take an additional continuation argument, then,
much as our factorial() example did, if the recursion
has reached its limit (the argument list is empty) it calls its
continuation on the empty list. Otherwise it has not finished, and
it evaluates its first component, passing a continuation that arranges
to evaluate the rest of the list by recursing:
76 sub map_eval { 77 my ($self, $env, $cont) = @_; 78 79 if (@$self) { 80 $self->first->Eval( 81 $env, 82 cont { 83 my ($evaluated_first) = @_; 84 $self->rest->map_eval( 85 $env, 86 cont { 87 my ($evaluated_rest) = @_; 88 $cont->Cont([$evaluated_first, 89 @$evaluated_rest]); 90 } 91 ); 92 } 93 ); 94 } else { 95 $cont->Cont([]); 96 } 97 }
This is the trickiest piece of code in the entire CPS re-write.
Fortunately having done it, it is useful in a number of other
scenarios. Now that we have map_eval() we can use it to re-write
PScm::SpecialForm::Primitive::Apply():
8 sub Apply { 9 my ($self, $form, $env, $cont) = @_; 10 11 $form->map_eval( 12 $env, 13 cont { 14 my ($ra_evaluated_args) = @_; 15 $cont->Cont($self->_apply(@$ra_evaluated_args)); 16 } 17 ); 18 }
Not too bad. The map_eval() is passed a continuation that
applies the primitive operation to the evaluated arguments and calls
the original argument continuation on the result.
It is worth noting again that there was no need to pass any continuation
to the individual private _apply() methods for each primitive,
so PScm::Primitive::Multiply etc. are unchanged.
The rest of the CPS transformations are much simpler, on the whole,
and others that require the rewriting of map can make use of
map_eval().
Next up is PScm::SpecialForm::Let, here's the changes:
13 sub Apply { 14 my ($self, $form, $env, $cont) = @_; 15 16 my ($bindings, $body) = $form->value; 17 my (@symbols, @values); 18 19 foreach my $binding ($bindings->value) { 20 my ($symbol, $value) = $binding->value; 21 push @symbols, $symbol; 22 push @values, $value; 23 } 24 25 $env->Extend( 26 \@symbols, 27 \@values, 28 cont { 29 my ($newenv) = @_; 30 $body->Eval($newenv, $cont); 31 } 32 ); 33 }
The changes are in bold on lines 14 and 27–31
If you remember, the old version at the end simply said
return $body->Eval($env->Extend(\@symbols, \@values));
Since we know that the call to $env->Extend() will
not return (those @values are still to be evaluated),
we instead have to pass a continuation that will accept
the resulting extended environment and evaluate the body in it. We have
already dealt with all the Eval() methods (They're all in
PScm::Expr) and they all take a continuation, so we pass the
original continuation argument, since the Eval() is the
expression that this Apply() was previously returning.
Remembering to add PScm::Env::Extend() to our list of
methods that will need looking at, we proceed to
PScm::SpecialForm::If::Apply(). We've already discussed how
to transform a conditional expression into CPS form, but since this
is our first encounter in the wild, let's refresh our memory by
first looking at the original non-cps version:
32 sub Apply { 33 my ($self, $form, $env) = @_; 34 35 my ($condition, $true_branch, $false_branch) = $form->value; 36 37 if ($condition->Eval($env)->isTrue) { 38 return $true_branch->Eval($env); 39 } else { 40 return $false_branch->Eval($env); 41 } 42 }
It evaluates the condition in the current env, and calls isTrue()
on the result, then uses that to decide whether to evaluate the true
branch or the false branch, both in the current environment.
Our CPS version is not that different:
41 sub Apply { 42 my ($self, $form, $env, $cont) = @_; 43 44 my ($condition, $true_branch, $false_branch) = $form->value; 45 46 $condition->Eval( 47 $env, 48 cont { 49 my ($result) = @_; 50 if ($result->isTrue) { 51 $true_branch->Eval($env, $cont); 52 } else { 53 $false_branch->Eval($env, $cont); 54 } 55 } 56 ); 57 }
It evaluates the condition in
the current environment and passes a continuation that will accept
the result. That continuation calls isTrue() on the result
and uses that to decide, in exactly the same way, whether to evaluate the
true branch or the false branch. In either case the original
continuation that was argument to PScm::SpecialForm::If::Apply()
is passed to the chosen branch's Eval() method.
Staying with the program, our next task is the invocation of lambda
handled by PScm::SpecialForm::Lambda::Apply():
65 sub Apply { 66 my ($self, $form, $env, $cont) = @_; 67 68 my ($args, $body) = $form->value; 69 70 $cont->Cont(PScm::Closure::Function->new($args, $body, $env)); 71 }
There's nothing very interesting here. lambda
just creates a closure. There are no calls to Eval() that
it must make during this creation, so we can treat the call to new
as a simple expression and invoke our argument
continuation on the result.
That just leaves PScm::Closure::Function::Apply()
and PScm::Env::Extend(). Let's start with
PScm::Closure::Function. The original just mapped
Eval() over its arguments then called a private _apply()
method on the results:
43 sub Apply { 44 my ($self, $form, $env) = @_; 45 46 my @evaluated_args = map { $_->Eval($env) } $form->value; 47 return $self->_apply(@evaluated_args); 48 }
Another job for map_eval() then:
44 sub Apply { 45 my ($self, $form, $env, $cont) = @_; 46 47 $form->map_eval( 48 $env, 49 cont { 50 my ($ra_evaluated_args) = @_; 51 $self->_apply($ra_evaluated_args, $cont); 52 } 53 ); 54 }
Note however that we need to pass the current continuation to
that private _apply() method. That's because the closure
will be calling Eval() on its body. Let's take a look at
PScm::Closure::_apply().
21 sub _apply { 22 my ($self, $ra_args, $cont) = @_; 23 24 my $extended_env = 25 $self->env->ExtendUnevaluated([$self->args], $ra_args); 26 return $self->body->Eval($extended_env, $cont); 27 }
It differs in that it takes a reference to an array of args and a
continuation, rather than just an array of args, and it passes the
continuation in to the call to Eval() on its body.
Finally, we need to rewrite PScm::Env::Extend().
15 sub Extend { 16 my ($self, $ra_symbols, $ra_values, $cont) = @_; 17 18 PScm::Expr::List->new(@$ra_values)->map_eval( 19 $self, 20 cont { 21 my ($ra_evaluated_values) = @_; 22 $cont->Cont( 23 $self->ExtendUnevaluated( 24 $ra_symbols, $ra_evaluated_values 25 ) 26 ); 27 } 28 ); 29 }
It uses map_eval() to evaluate its list of values, passing
the result to a continuation that extends the environment with those
values. It calls the argument continuation $cont on the
result.
At this point in the discussion, we have a working CPS version of interpreter 0.0.2, and all the original tests that were written for that version still pass. However we seem to have done a lot of hard work for no benefit, since the interpreter is externally equivalent to the original 0.0.2 version. We can remedy that by giving the interpreter an additional construct that provides direct access to the underlying continuations.
There are many ways that this could be done, but one of the
best-known and most powerful ways is with a form that goes by the
unwieldy title call-with-current-continuation,
usually abbreviated to call/cc. This form takes
a function as argument and calls it, passing the current continuation
as an explicit argument to the function, for example:
> (call/cc (lambda (cont) (cont 10))) 10
When the function invokes the continuation as a function, control
returns to the call/cc and the argument to the continuation
becomes the result of the call to call/cc.
If the previous example doesn't seem too exciting, how about this:
> (call/cc > (lambda (cont) > (if (cont 10) > 20 > 30))) 10
Here the call to (cont 10) produced an immediate return
of the value 10 through the call/cc even though
it was executed in the conditional position of an if
statement.
These two examples only show control passing down the “stack” when a continuation is invoked. However it is perfectly reasonable for control to return up the stack to a procedure that has already returned. It is simply not easy to demonstrate with this version of the interpreter. Once we have an interpreter with assignment and sequences, it becomes much easier.
call/cc is in fact a low-level, if not the lowest level
continuation tool. It is possible to build higher level control
constructs using it. Abandoning pscheme for a moment, consider this
fibonacci40
sequence generator in some hypothetical Perl-like language that
supports co-routines:
sub fib {
my ($i, $j) = (0, 1);
for (;;) {
yield $i;
($i, $j) = ($j, $i + $j);
}
}
while ((my $i = fib()) < 22) { # prints 0 1 2 3 5 8 13 21
print "$i ";
}
That yield call not only behaves like a return statement,
but also remembers the current state of the function so that
the next time the function is called control resumes where it last left off.
With built in continuations this sort of control
flow is very easy to achieve.
Anyway I hope this has whet your appetite a little for what
call/cc can do, so let's have a look at its implementation.
It is of course a special form, and as usual it has an Apply() method:
74 package PScm::SpecialForm::CallCC; 75 76 use base qw(PScm::SpecialForm); 77 use PScm::Closure; 78 use PScm::Continuation; 79 80 sub Apply { 81 my ($self, $form, $env, $cont) = @_; 82 83 $form->first->Eval( 84 $env, 85 cont { 86 my ($closure) = @_; 87 $closure->Apply(new PScm::Expr::List($cont), 88 $env, $cont); 89 } 90 ); 91 } 92 93 1;
It evaluates its first argument, which should result in a function of
one argument, passing the Eval() a continuation which will
Apply() the function to a form explicitly containing the current
continuation. It also passes the current env and the current
continuation a second time, this time as the normal implicit
argument.
That's all there is to it. Of course the continuation itself will
need an Apply() method so that it can be invoked as an operator.
We're now ready to see the whole of the PScm::Continuation package, in Listing 24.
PScm/Continuation.pm1 package PScm::Continuation; 2 3 use strict; 4 use warnings; 5 use base qw(PScm); 6 7 require Exporter; 8 9 our @ISA = qw(PScm Exporter); 10 11 our @EXPORT = qw(cont); 12 13 sub new { 14 my ($class, $cont) = @_; 15 bless { cont => $cont }, $class; 16 } 17 18 sub cont(&) { 19 my ($cont) = @_; 20 return __PACKAGE__->new($cont); 21 } 22 23 sub Apply { 24 my ($self, $form, $env, $cont) = @_; 25 $form->map_eval( 26 $env, 27 cont { 28 my ($ra_evaluated_args) = @_; 29 $self->Cont($ra_evaluated_args->[0]); 30 } 31 ); 32 } 33 34 sub Cont { 35 my ($self, $arg) = @_; 36 return cont { $self->{cont}->($arg) }; 37 } 38 39 sub Bounce { 40 my ($self) = @_; 41 $self->{cont}->(); 42 } 43 44 sub Eval { 45 my ($self, $env, $cont) = @_; 46 $cont->Cont($self); 47 } 48 49 1;
We've already seen most of this, only the Apply()
method is new.
23 sub Apply { 24 my ($self, $form, $env, $cont) = @_; 25 $form->map_eval( 26 $env, 27 cont { 28 my ($ra_evaluated_args) = @_; 29 $self->Cont($ra_evaluated_args->[0]); 30 } 31 ); 32 }
Apply() on
lines 23–32
is another method that makes use of map_eval()
to evaluate its arguments. It passes it a continuation that
calls itself on the first of its evaluated arguments, totally
ignoring the passed-in, current continuation, and effecting
transfer of control to whatever context this continuation
represents.
And we're done.
t/PScm_CallCC.t1 use strict; 2 use warnings; 3 use Test::More; 4 use lib './t/lib'; 5 use PScm::Test tests => 2; 6 7 BEGIN { use_ok('PScm') } 8 9 eval_ok(<<EOF, '10', 'call/cc'); 10 (let ((a (lambda (return) 11 (if (return (* 2 5)) 12 20 13 30)))) 14 (call/cc a)) 15 EOF 16 17 # vim: ft=perl
A simple test of call/cc can be seen in
Listing 25.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.2.tgz
letrecThe interpreter version 0.0.3 back in Chapter 6
introduced letrec (let recursive)
which allowed environments to be created in such a way that closures
would extend the environment that they were themselves defined in,
allowing them to make recursive calls.
This subsection takes the additions to version 0.0.3 and reimplements
them in CPS. We're going to start to pick up the pace somewhat from
hereon in, but I'll still present all of the changes, starting with
the letrec special form itself. Here's the original v3:
40 sub Apply { 41 my ($self, $form, $env) = @_; 42 43 my ($ra_symbols, $ra_values, $body) = $self->UnPack($form, $env); 44 45 return $body->Eval( 46 $env->ExtendRecursively($ra_symbols, $ra_values)); 47 }
The CPS version calls a modified
PScm::Env::ExtendRecursively(),
passing a continuation that takes the recursively extended environment
and evaluates the body in it, passing the original continuation to that
Eval().
49 sub Apply { 50 my ($self, $form, $env, $cont) = @_; 51 52 my ($ra_symbols, $ra_values, $body) = $self->UnPack($form); 53 54 $env->ExtendRecursively( 55 $ra_symbols, 56 $ra_values, 57 cont { 58 my ($extended_env) = @_; 59 $body->Eval($extended_env, $cont); 60 } 61 ); 62 }
PScm::Env::ExtendRecursively() calls
PScm::Env::ExtendUnevaluated() as a simple
expression then calls _eval_values() on
the extended environment, passing the original continuation:
41 sub ExtendRecursively { 42 my ($self, $ra_symbols, $ra_values, $cont) = @_; 43 44 my $newenv = $self->ExtendUnevaluated($ra_symbols, $ra_values); 45 $newenv->_eval_values($cont); 46 }
Here's the new CPS _eval_values():
48 sub _eval_values { 49 my ($self, $cont) = @_; 50 $self->_map_bindings([keys %{ $self->{bindings} }], $cont); 51 }
It uses a new helper _map_bindings(),
where the original _eval_values() just used
map. This works in a similar way to
map_eval(), evaluating each value in the
environment but then assigning the result back to the original
binding:
53 sub _map_bindings { 54 my ($self, $ra_keys, $cont) = @_; 55 my (@keys) = @$ra_keys; 56 if (@keys) { 57 my $firstkey = shift @keys; 58 $self->{bindings}{$firstkey}->Eval( 59 $self, 60 cont { 61 my ($value) = @_; 62 $self->{bindings}{$firstkey} = $value; 63 $self->_map_bindings([@keys], $cont); 64 } 65 ); 66 } else { 67 $cont->Cont($self); 68 } 69 }
Other methods are unchanged so we have completed the CPS
rewrite of letrec, and all tests for 0.0.3 still pass in 0.1.3.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.3.tgz
let*The interpreter version 0.0.4 back in Chapter 7
added let*, a shorthand way of creating nested
environments providing the appearence of sequential assignment
within the bindings of the let* expression.
This was a simple addition, the rewrite will be
equally simple.
Here's the new PScm::SpecialForm::LetStar::Apply():
70 sub Apply { 71 my ($self, $form, $env, $cont) = @_; 72 73 my ($ra_symbols, $ra_values, $body) = $self->UnPack($form); 74 75 $env->ExtendIteratively( 76 $ra_symbols, 77 $ra_values, 78 cont { 79 my ($extended_env) = @_; 80 $body->Eval($extended_env, $cont); 81 } 82 ); 83 }
Just like letrec (which called a modified
PScm::Env::ExtendRecursively(),) this calls
a modified ExtendIteratively(), passing
a continuation that evaluates the body of the let*
in the new environment with the original continuation.
Here's the modifications to
PScm::Env::ExtendIteratively():
48 sub ExtendIteratively { 49 my ($self, $ra_symbols, $ra_values, $cont) = @_; 50 my @symbols = @$ra_symbols; 51 my @values = @$ra_values; 52 if (@symbols) { 53 my $symbol = shift @symbols; 54 my $value = shift @values; 55 $self->Extend( 56 [$symbol], 57 [$value], 58 cont { 59 my ($extended) = @_; 60 $extended->ExtendIteratively([@symbols], [@values], 61 $cont); 62 } 63 ); 64 } else { 65 $cont->Cont($self); 66 } 67 }
The old version just iterated over the name/value pairs,
creating an additional nested environment each time around the
loop and returning the final result.
CPS is easier with recursive definitions so this
ExtendIteratively() has been recast as a
recursive method. It still does the same job, but additionally
arranges that the original continuation gets called on the final,
extended environment.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.4.tgz
Our next iteration of the interpreter, version 0.0.5
back in Chapter 8, added the list manipulation
functions
quote,
list,
car,
cdr and
cons
to the language, and additionally changed the
internal implementation of PScm::Expr::List
from simple perl listrefs to linked lists,
making PScm::Expr::List abstract, adding
a PScm::Expr::List::Pair class to represent
the cons cells, and adding
a PScm::Expr::List::Null class to represent the
empty list.
Surprisingly, The CPS rewrite of all of this is quite minimal.
First, here's the new
quote in PScm::SpecialForm::Quote::Apply():
157 sub Apply { 158 my ($self, $form, $env, $cont) = @_; 159 $cont->Cont($form->first); 160 }
The original returned its first argument unevaluated, the CPS form calls
its continuation on it. Remember that the quote system
was re-written for a later version of the interpreter to support
unquote back in Section 9.2.2, so we'll be returning
to quote later on, in
Section 13.6.6, where we rewrite that rewrite!
The other additional functions: car, cdr, cons and list
are all primitives that
share an Apply() method that has already been rewritten into CPS in
Section 13.6.2.
Among the PScm::Expr classes, the only thing that changes
is the map_eval() method. That method was introduced in version
0.0.5 to work with pscheme lists, then re-introduced at an earlier stage
of the CPS rewrite, in version 0.1.2, because we needed a recursive
alternative to Perl's map. Finally, here, we combine the two
implementations. Here's PScm::Expr::List::Pair::map_eval():
132 sub map_eval { 133 my ($self, $env, $cont) = @_; 134 135 $self->first->Eval( 136 $env, 137 cont { 138 my ($evaluated_first) = @_; 139 $self->rest->map_eval( 140 $env, 141 cont { 142 my ($evaluated_rest) = @_; 143 $cont->Cont($self->Cons($evaluated_first, 144 $evaluated_rest)); 145 } 146 ); 147 } 148 ); 149 }
And here's the new default PScm::Expr::map_eval() that both
terminates the recursion of map_eval() if $self is
PScm::Expr::Null, does the right thing if the cdr
of the list is not a list, and handles continuations, all in one tiny
method:
34 sub map_eval { 35 my ($self, $env, $cont) = @_; 36 $self->Eval($env, $cont); 37 }
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.5.tgz
macro and unquoteVersion 0.0.6 of our interpreter, from Chapter 9,
introduced the macro special form. This special form
took arguments in an identical manner to lambda and created
a variant type of closure PScm::Closure::Macro.
Normal lambda closure evaluation proceeds by evaluating the arguments
to the closure then evaluating the body of the closure with
those arguments bound. In contrast macro closure evaluation
proceeds by evaluating the body of the closure with its
unevaluated arguments bound, then re-evaluating the result.
The rewrite into CPS is trivial, first here's the CPS
form of PScm::SpecialForm::Macro::Apply():
175 sub Apply { 176 my ($self, $form, $env, $cont) = @_; 177 my ($args, $body) = $form->value; 178 $cont->Cont(PScm::Closure::Macro->new($args, $body, $env)); 179 }
Just as with PSCm::SpecialForm::Lambda::Apply(),
the creation of the closure can be treated as a simple expression
(no calls to Eval()) and the continuation called on the result.
Now PScm::Closure::Macro::Apply():
62 sub Apply { 63 my ($self, $form, $env, $cont) = @_; 64 65 $self->_apply( 66 $form, 67 cont { 68 my ($new_form) = @_; 69 $new_form->Eval($env, $cont); 70 } 71 ); 72 }
Here we pass a continuation to the core
_apply() method that takes the resulting
new form and evaluates that in the current environment
with the current continuation as an additional argument.
The core _apply() extends the environment with
unevaluated arguments, then calls the body of the macro with the
new environment and the passed in continuation.
17 sub _apply { 18 my ($self, $args, $cont) = @_; 19 20 my $extended_env = 21 $self->{env}->ExtendUnevaluated($self->{args}, $args); 22 $self->{body}->Eval($extended_env, $cont); 23 }
But you get the idea.
That's all there is to the rewrite of the macro extension
into CPS. However Chapter 9 also rewrote
PScm::SpecialForm::Quote to support the unquote
keyword which allows the interpolation of evaluated sub-expressions within
a quoted expression. That proves more interesting to recast into CPS.
Let's start at the top by looking at the new CPS version of
PScm::SpecialForm::Quote::Apply():
186 sub Apply { 187 my ($self, $form, $env, $cont) = @_; 188 $form->first->Quote($env, $cont); 189 }
So far so good, we just pass the current continuation along with the
current environment to the Quote() method of whatever
expression we're quoting.
Let's deal with the easy stuff first. PScm::Expr::Quote()
used to just return $self, the CPS version calls the continuation
on $self instead:
41 sub Quote { 42 my ($self, $env, $cont) = @_; 43 $cont->Cont($self); 44 }
That leaves PScm::Expr::List::Pair's Quote():
165 sub Quote { 166 my ($self, $env, $cont) = @_; 167 if ($self->first->is_unquote) { 168 $self->rest->first->Eval($env, $cont); 169 } else { 170 $self->quote_rest($env, $cont); 171 } 172 }
Great! since the calls to both Eval() and quote_rest()
are in tail position, it need only pass the continuation along to both.
All the
Eval() methods have already been dealt with of course, so that leaves
quote_rest(). Let's first refresh our memories by
looking at the non-CPS original:
144 sub quote_rest { 145 my ($self, $env) = @_; 146 return $self->Cons( 147 $self->first->Quote($env), 148 $self->rest->quote_rest($env) 149 ); 150 }
This is definately not tail recursive. But if we
think it through there are no problems. The first thing it does is
call Quote() on its first() element,
then it calls itself on the rest() of the list, then
finally it calls Cons() on those two results. Both
the call to Quote() and quote_rest()
could potentially result in calls to Eval() so we need to pass
continuations to both. We can rewrite it a little first to make
the order of operations more explicit:
sub quote_rest {
my ($self, $env) = @_;
my $quoted_first = $self->first->Quote($env);
my $quoted_rest = $self->rest->quote_rest($env);
return $self->Cons($quoted_first, $quoted_rest);
}
Now all we do is rewrite that so that the call to
Quote() gets a continuation that performs the remaining
two operations, including passing a second continuation to
quote_rest() that performs the last Cons().
here's the CPS rewrite:
174 sub quote_rest { 175 my ($self, $env, $cont) = @_; 176 $self->first->Quote( 177 $env, 178 cont { 179 my ($quoted_first) = @_; 180 $self->rest->quote_rest( 181 $env, 182 cont { 183 my ($quoted_rest) = @_; 184 $cont->Cont( 185 $self->Cons($quoted_first, $quoted_rest)); 186 } 187 ); 188 } 189 ); 190 }
It calls Quote() on its first element, passing
a continuation
(lines 178–188)
that accepts the $quoted_first and then calls
quote_rest() on the rest of the elements, passing
that a continuation
(lines 182–186)
that accepts the $quoted_rest and
calls the original continuation on the result of Cons()-ing
the $quoted_first and $quoted_rest together.
Finally, as before, where the default PScm::Expr::quote_rest()
just returned $self, now it calls its aregument continuation
on $self:
46 sub quote_rest { 47 my ($self, $env, $cont) = @_; 48 $cont->Cont($self); 49 }
That's it for our CPS rewrite of the unquote facility.
All other methods are unchanged.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.6.tgz
Next up are the sequences (begin) and assignment
(set!) introduced by interpreter 0.0.7 in Chapter 10.
Let's start with sequences and the begin special form.
To recap begin takes a sequence of zero or more expressions
and evaluates them in strict left to right order, returning the last result.
If given no arguments, in this implementation it returns the empty list.
Here's its Apply():
215 sub Apply { 216 my ($self, $form, $env, $cont) = @_; 217 if ($form->is_pair) { 218 $self->apply_next($form, $env, $cont); 219 } else { 220 $cont->Cont($form); 221 } 222 }
The original was iterative. This version has been recast in a recursive
mould to make the CPS transform easier and to take advantage of
PScm::Expr::List. If the list is empty it calls the continuation
on the empty list, otherwise it passes the form, environment and
continuation to a helper method apply_next():
224 sub apply_next { 225 my ($self, $form, $env, $cont) = @_; 226 227 $form->first->Eval( 228 $env, 229 cont { 230 my ($val) = @_; 231 if ($form->rest->is_pair) { 232 $self->apply_next($form->rest, $env, $cont); 233 } else { 234 $cont->Cont($val); 235 } 236 } 237 ); 238 }
It evaluates the first element of the list, passing a continuation
that accepts the result. If there is more of the list to process,
it calls itself recursively on the rest of the list, otherwise it
calls the original continuation on the $val (the value
of the last expression on the list). Note the similarity between
this method and map_eval(). The diference is only that apply_next()
does not need to construct a new list of all the evaluated results.
Next and last is set!. set! uses
PScm::Env::Assign() that was developed for
letrec to locate the nearest binding for a
symbol and change its value. set! is a special
form since it evaluates its second argument (the value)
but not its first (the symbol).
197 sub Apply { 198 my ($self, $form, $env, $cont) = @_; 199 my ($symbol, $expr) = $form->value; 200 $expr->Eval( 201 $env, 202 cont { 203 my ($val) = @_; 204 $cont->Cont($env->Assign($symbol, $val)); 205 } 206 ); 207 }
The CPS rewrite is pretty straightforward. It evaluates the value passing a continuation that will perform the assignment (a simple expression) calling the original continuation on the result.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.7.tgz
defineVersion 0.0.8 in Chapter 11 finally introduced
define, delayed until then for reasons I won't
reiterate here. Akin to set!, define
takes a symbol and a value and binds the symbol to the
value in the current environment. It is a special form
since it does not evaluate the symbol. The CPS rewrite
of PScm::SpecialForm::Define::Apply()
proceeds much as the one for set! did:
246 sub Apply { 247 my ($self, $form, $env, $cont) = @_; 248 my ($symbol, $expr) = $form->value; 249 250 $expr->Eval( 251 $env, 252 cont { 253 my ($value) = @_; 254 $cont->Cont($env->Define($symbol, $value)); 255 } 256 ); 257 }
It evaluates the expression, passing a continuation that accepts
the result and calls PScm::Env::Define() to bind
the result to the symbol in the current environment. We can treat
the call to PScm::Env::Define() as a simple expression
and just call the original continuation on the result.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.8.tgz
Version 0.0.9 in Chapter 12 introduced an object-oriented
extension to PScheme, by means of the make-class
special form and the root parent class. Although there was
a fair amount of code added to implement that extension, it turns
out that very little of that code needs changing to produce a
CPS version. As usual we just have to hunt down the calls to
Eval() and ensure that there is a continuation available to pass
in. Let's start with PScm::SpecialForm::MakeClass::Apply().
265 sub Apply { 266 my ($self, $form, $env, $cont) = @_; 267 268 my $parent_expr = $form->first; 269 my $fields = $form->rest->first; 270 my $methods = $form->rest->rest; 271 272 $parent_expr->Eval( 273 $env, 274 cont { 275 my ($parent_class) = @_; 276 $cont->Cont( 277 PScm::Class->new( 278 $parent_class, $fields, $methods, $env 279 ) 280 ); 281 } 282 ); 283 }
The first thing the old version did was to evaluate the parent expression
(the value of the parent class) then use that along with the fields
and methods (unevaluated) to create the new class. Our rewrite
evaluates the parent expression passing a continuation that will
create the class. We can treat the class creation as a simple expression
(it makes no further calls to Eval()) and just call the original
continuation on the result.
Nothing to follow up on there, so next we turn our attention to the
application of a class to arguments, which creates a new object.
This is in PScm::Class::Apply():
33 sub Apply { 34 my ($self, $form, $env, $cont) = @_; 35 36 my $new_object = $self->make_instance(); 37 $new_object->call_method( 38 $new_object, 39 "init", $form, $env, 40 cont { 41 $cont->Cont($new_object); 42 } 43 ); 44 }
As usual, Apply() now takes a continuation. The old version
called make_instance() to create a new instance of the
class, then called the init method of the new object with
the arguments to the class, then returned the new object. The CPS
version can still just call make_instance() as a
simple expression, but needs to pass a continuation to
call_method() because
call_method() will be calling Eval() on both the
arguments and the body of the method. The continuation just calls
the original continuation on the new object (as if it were returning it).
Remembering that objects in this implementation are just
environments, Here's the rewrite of PScm::Env::call_method():
183 sub call_method { 184 my ($self, $this, $method_name, $args, $env, $cont) = @_; 185 186 if (my $method = $self->_lookup_method($method_name)) { 187 $method->ApplyMethod($this, $args, $env, $cont); 188 } else { 189 $cont->Cont(undef); 190 } 191 }
Hey, this isn't too bad at all. If call_method()
finds the method, it calls
ApplyMethod() on it, passing the original continuation
as an extra argument. Wheras the old version implicitly returned
undef if the method was not found, the CPS version must
explicitly call the continuation on undef41.
Next we need to look at
PScm::Closure::Method::ApplyMethod():
96 sub ApplyMethod { 97 my ($self, $this, $form, $env, $cont) = @_; 98 99 $form->map_eval( 100 $env, 101 cont { 102 my ($evaluated_args) = @_; 103 $self->_apply( 104 PScm::Expr::List->Cons($this, $evaluated_args), 105 $cont); 106 } 107 ); 108 }
Again we use map_eval() on the $form
(the arguments to the method) to evaluate them, this time passing
a continuation that applies the method to its evaluated arguments,
using PScm::Expr::List::Cons() to prepend the current
object $this to the PScm::Expr::List of arguments
to the core PScm::Closure::_apply() method, and passing in the original
continuation.
We've already discussed that core _apply() method
in Section 13.6.2 when we re-wrote lambda.
That just leaves the calling of methods on the objects themselves.
Both PScm::Env and PScm::Env::Super have an
Apply() method. The one from PScm::Env::Super arranges
to pass the current value of this to the called method,
otherwise they are very similar. Here's
PScm::Env::Apply():
193 sub Apply { 194 my ($self, $form, $env, $cont) = @_; 195 196 my ($method, $args) = ($form->first, $form->rest); 197 $self->CallMethodOrDie($self, $method, $args, $env, $cont); 198 }
And here's PScm::Env::Super::Apply():
222 sub Apply { 223 my ($self, $form, $env, $cont) = @_; 224 225 my ($method, $args) = ($form->first, $form->rest); 226 my $this = $env->LookUp(PScm::Expr::Symbol->new("this")); 227 $self->CallMethodOrDie($this, $method, $args, $env, $cont); 228 }
They both now make use of a new support method
PScm::Env::CallMethodOrDie() which just does
what it says.
200 sub CallMethodOrDie { 201 my ($self, $this, $method, $args, $env, $cont) = @_; 202 $self->call_method( 203 $this, 204 $method->value, 205 $args, $env, 206 cont { 207 my ($res) = @_; 208 if (defined $res) { 209 $cont->Cont($res); 210 } else { 211 die "method ", $method->value, " not found\n"; 212 } 213 } 214 ); 215 }
It calls call_method() on $self
and passes a continuation that checks if the result is defined.
If the result is defined that means that call_method()
sucessfully found the method and invoked it, in which case the original
continuation is called on the result. If the result
is undef then the method was not found and
CallMethodOrDie() lives up to its name.
To make some of the subsequent tests easier I've
added a print primitive. It takes a single evaluated
argument and calls its Print() method. The only problem
to solve is how to tell it about the current output filehandle.
Ideally we would create a new PScm::Expr::FileHandle
type and install one containing the default output filehandle
in the environment for print to find, however it
is easier for our limited purposes to just pass the output
filehandle to the PScm::SpecialForm::Print constructor.
You can see this in the changes to ReadEvalPrint()
between 0.0.9 and 0.1.9 here:
33 sub ReadEvalPrint { 34 my ($infh, $outfh) = @_; 35 36 $outfh ||= new FileHandle(">-"); 37 my $reader = new PScm::Read($infh); 38 my $initial_env; 39 $initial_env = new PScm::Env( 40 let => new PScm::SpecialForm::Let(), 41 '*' => new PScm::Primitive::Multiply(), 42 '-' => new PScm::Primitive::Subtract(), 43 '+' => new PScm::Primitive::Add(), 44 if => new PScm::SpecialForm::If(), 45 lambda => new PScm::SpecialForm::Lambda(), 46 list => new PScm::Primitive::List(), 47 car => new PScm::Primitive::Car(), 48 cdr => new PScm::Primitive::Cdr(), 49 cons => new PScm::Primitive::Cons(), 50 letrec => new PScm::SpecialForm::LetRec(), 51 'let*' => new PScm::SpecialForm::LetStar(), 52 eval => new PScm::SpecialForm::Eval(), 53 macro => new PScm::SpecialForm::Macro(), 54 quote => new PScm::SpecialForm::Quote(), 55 'set!' => new PScm::SpecialForm::Set(), 56 begin => new PScm::SpecialForm::Begin(), 57 define => new PScm::SpecialForm::Define(), 58 'make-class' => new PScm::SpecialForm::MakeClass(), 59 'call/cc' => new PScm::SpecialForm::CallCC(), 60 print => new PScm::SpecialForm::Print($outfh), 61 ); 62 63 $initial_env->Define( 64 PScm::Expr::Symbol->new("root"), 65 PScm::Class::Root->new($initial_env) 66 ); 67 trampoline(cont { repl($initial_env, $reader, $outfh) }); 68 }
The PScm::SpecialForm::Print package is unusual, therefore, in
that it has a new() method and creates its own instance,
because it needs to save the argument filehandle. Other than that it is
a standard CPS special form:
286 package PScm::SpecialForm::Print; 287 288 use base qw(PScm::SpecialForm); 289 290 use PScm::Continuation; 291 292 sub new { 293 my ($class, $outfh) = @_; 294 bless { outfh => $outfh }, $class; 295 } 296 297 sub Apply { 298 my ($self, $form, $env, $cont) = @_; 299 $form->first->Eval($env, cont { 300 my ($thing) = @_; 301 $thing->Print( 302 $self->{outfh}, 303 cont { 304 $cont->Cont($thing) 305 } 306 ); 307 }); 308 } 309 310 1;
PScm::SpecialForm::Print::Apply()
invokes its argument $form's Eval() method with
the current environment and a continuation that will print the result,
then call the original continuation on the evaluated result. So
print returns the expression that it printed.
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.1.9.tgz
We're done! Let's play around with what we have.
error HandlerThere are many uses of
call/cc, the simplest is probably the
definition of escape procedures, procedures
that when called, escape the current context
and return control to a containing outer context. The
simplest type of escape procedure is error.
If at any point in your code you invoke error,
the argument error message is printed,
the current context is abandoned and control is
returned to the top level. For example (pretending
we have a divide “/” operator):
> (define div > (lambda (numerator denominator) > (if denominator > (/ numerator denominator) > (error "division by zero")))) div > (+ (div 2 0) 1) Error: division by zero () >
The addition never happened. Control returned directly to the
top level.
Using call/cc, we can define an
error escape procedure in the
PScheme language itself, without needing to
make further changes to the interpreter.
All error has to do is to print its error message
and call a continuation that returns control to the
top level. So, assuming that top level continuation is already
installed as ^escape (I'm just using a caret, “^”,
to prefix any continuation names so they stand out,)
the error procedure
itself is straightforward:
(define error
(lambda (msg)
(begin
(print msg)
(^escape ()))))
Note that the ^escape continuation expects an
argument, so error passes the empty list (),
and that is what the repl prints as the result of whatever
expression error is called from.
Next we need to create that top level continuation. Here's a first attempt:
(define ^escape (call/cc (lambda (c) c)))
This looks promising. The call/cc calls the
anonymous lambda expression passing in the current continuation.
The lambda expression just returns its argument, which is what
call/cc returns, and that is what gets bound to the
global ^escape.
This is good, as far as it goes, the current continuation
certainly is bound to ^escape.
The problem is that the operation of defining
^escape is part of the continuation
saved in ^escape. Put another way, the first time
error calls ^escape, control resumes
at the point that call/cc is returning its value
and so the define is re-executed, binding the empty list
to ^escape and forgetting the previously bound
continuation. So the ^escape continuation is
only useable once.
There are two ways to fix this.
The first way would be to change error so that it passes
^escape as argument to itself: (^escape ^escape),
The downside of that is that you will get a
PScm::Continuation printed out as the result of any
call to error.
The other way to fix this is to change the way we set up
^escape in the first place. First of all we create
a global ^escape variable with an arbitrary initial
binding:
(define ^escape 0)
Then we use call/cc as before but call an expression that
directly assigns to ^escape:
(call/cc
(lambda (cont)
(begin
(set! ^escape cont))))
This way the call/cc has no enclosing context, no
deferred operations to perform, and when ^escape is
invoked control returns directly to the top level.
A test of the error handler, which just duplicates
the above code, is in Listing 26.
t/CPS_Error.t1 use strict; 2 use warnings; 3 use Test::More; 4 use lib 't/lib'; 5 use PScm::Test tests => 2; 6 7 BEGIN { use_ok('PScm') } 8 9 eval_ok(<<EOF, <<EOR, 'error'); 10 (define ^error 0) 11 (call/cc 12 (lambda (cont) 13 (begin 14 (set! ^error cont)))) 15 16 (define error 17 (lambda (msg) 18 (begin 19 (print msg) 20 (^error ())))) 21 22 (define div 23 (lambda (numerator denominator) 24 (if denominator 25 (/ numerator denominator) 26 (error "division by zero")))) 27 28 (+ (div 2 0) 1) 29 30 EOF 31 ^error 32 PScm::Continuation 33 error 34 div 35 "division by zero" 36 () 37 EOR 38 39 # vim: ft=perl
Next let's try something a bit more challenging.
yieldRemember that strange fibonacci
generator that was described
towards the end of Section 13.6.2, the one that used
a hypothetical yield command to return a value while
remembering its current position so that a subsequent call
to the function would resume where it left off? Well here's
how we'd like to write it in PScheme:
(define fib
(yielder
(letrec ((fib-loop
(lambda (i j)
(begin
(yield i)
(fib-loop j (+ i j))))))
(fib-loop 0 1))))
and here's how we'd like to call it:
(let ((n 10))
(while n
(begin
(set! n (- n 1))
(print (fib)))))
Note that there is nothing at all special about the code that
uses fib. All of the interesting details are in
the definition of fib itself.
The function fib is defined as a yielder (my term).
It creates a recursive helper routine fib-loop and calls it
with arguments 0 and 1. That helper routine
yields the current value of its first argument i,
then calls itself with argument i replaced by j and
j replaced with i + j.
The second part of the example loops 10 times printing the next
value from fib each time around the loop.
Of course this presupposes a few features that PScheme doesn't appear
to have. The while macro was already introduced in
Section 9.2.2, but here it is again just for completeness:
(define while
(macro (test body)
'(letrec
((loop
(lambda ()
(if ,test
(begin
,body
(loop))
()))))
(loop))))
You can see that it's a recursive definition, but by now that
shouldn't worry you: as each call to loop is in tail
position we won't grow any context or eat any stack with this
definition.
The other two features we don't have yet are yield
and yielder. yield is actually quite
easy to write. When we say (yield value), what we
really want to do is return not only the value, but also the
current continuation so that the next time we are called
that continuation can be called instead, returning us to
where we left off. We can return more than one value
by wrapping the values in a list, so notionally
(yield value) means:
(^return (list current-continuation value))
where ^return is another continuation set up by
the caller of the function.
Now we need a way of getting the current continuation
and the only way to do that is with call/cc
so, still notionally, but getting closer,
(yield value) means:
(call/cc
(lambda (current-continuation)
(^return (list current-continuation value))))
In fact that's it, all we need to do is wrap that up in a macro,
and we have yield:
(define yield
(macro (value)
'(call/cc
(lambda (^here)
(^return (list ^here ,value))))))
Next we need to look at yielder. You probably won't
be surprised to find out it's another macro.
It returns a function that, when called for the
first time, invokes the body of the yielder expression,
saving the current continuation in a ^return
variable. When yield is invoked control returns
through the ^return continuation. The ^here
continuation part of the returned result is saved and the value
part is returned by the function as a whole.
On subsequent calls, rather than invoking the body of the yielder
again, the saved ^here continuation is invoked, returning control
to where the yield left off.
Here's yielder:
(define yielder
(macro (body)
'(let ((firsttime 1)
(^resume 0)
(^return 0))
(lambda ()
(if firsttime
(let ((res (call/cc
(lambda (^cont)
(begin
(set! ^return ^cont)
,body)))))
(begin
(set! firsttime 0)
(set! ^resume (car res))
(car (cdr res))))
(let ((res (call/cc
(lambda (^cont)
(begin
(set! ^return ^cont)
(^resume))))))
(begin
(set! ^resume (car res))
(car (cdr res)))))))))
Again, continuations are flagged with a caret.
That really is all there is to it. If this seems like a solution
looking for a problem, then let me point out a very real problem for
which this would be the perfect solution. Consider the venerable
File::Find package from the core Perl distribution.
This package allows you to specify criteria for recursively locating
files in a filesystem, along with a callback subroutine which is
called on each file so located. Sometimes this is exactly what you
need, but sometimes you would prefer File::Find to behave
as an iterator, returning the next file found on each
call. With proper support for co-routines in perl, the callback
function that you provide to File::Find need only
yield the file to achieve exactly that, without changing
a single line of the File::Find package itself!
Tests for this yield feature, which just duplicate
the above code, are in Listing 27.
t/CPS_Yield.t1 use strict; 2 use warnings; 3 use Test::More; 4 use lib 't/lib'; 5 use PScm::Test tests => 2; 6 7 BEGIN { use_ok('PScm') } 8 9 eval_ok(<<EOF, <<EOR, 'yield'); 10 (define yield 11 (macro (value) 12 '(call/cc 13 (lambda (^here) 14 (^return (list ^here ,value)))))) 15 16 (define yielder 17 (macro (body) 18 '(let ((firsttime 1) 19 (^resume 0) 20 (^return 0)) 21 (lambda () 22 (if firsttime 23 (let ((res (call/cc 24 (lambda (^cont) 25 (begin 26 (set! ^return ^cont) 27 ,body))))) 28 (begin 29 (set! firsttime 0) 30 (set! ^resume (car res)) 31 (car (cdr res)))) 32 (let ((res (call/cc 33 (lambda (^cont) 34 (begin 35 (set! ^return ^cont) 36 (^resume)))))) 37 (begin 38 (set! ^resume (car res)) 39 (car (cdr res))))))))) 40 41 (define while 42 (macro (test body) 43 '(letrec 44 ((loop 45 (lambda () 46 (if ,test 47 (begin 48 ,body 49 (loop)) 50 ())))) 51 (loop)))) 52 53 (define fib 54 (yielder 55 (letrec ((fib-loop 56 (lambda (i j) 57 (begin 58 (yield i) 59 (fib-loop j (+ i j)))))) 60 (fib-loop 0 1)))) 61 62 (let ((n 10)) 63 (while n 64 (begin 65 (set! n (- n 1)) 66 (print (fib))))) 67 EOF 68 yield 69 yielder 70 while 71 fib 72 0 73 1 74 1 75 2 76 3 77 5 78 8 79 13 80 21 81 34 82 () 83 EOR 84 85 # vim: ft=perl
This has been a long chapter and a difficult one, particularily if you were unfamiliar with the subject of continuations. It has however provided numerous real-world examples of CPS during the rewrite of the interpreter and hopefully the basic principles of CPS have been well covered.
To reiterate the basic idea, continuations can be thought of as the “rest of the computation”, or perhaps more graphically as a “reference to a return statement” that can be called as a function.
Anyway, having achieved a CPS interpreter in
Section 13.6.2
we then introduced the call/cc form, which
passes the current continuation to its argument function.
If Perl functions could take a reference to their return
statement with a syntax like \return, then
we could write call/cc in perl like this:
sub call_cc {
my ($sub) = @_;
$sub->(\return);
}
Unfortunately Perl 5 does not support that syntax yet, but lest you think this is all irrelevant to Perl, you should be aware that the Parrot virtual machine which will run Perl6 has continuations built in from the ground up!
Finally, having completely re-worked the interpreter in CPS,
in
Section 13.7
we showed how we could use call/cc in conjunction with
macro to create two high-level control constructs:
error and yield from within the PScheme
language itself.
The next few chapters will take continuations a little further, to show the sorts of things that can be done by varying the internal details of the implementation of continuations.
sub { times($n, shift, $ret) }
where times() is
sub times {
my ($x, $y, $ret) = @_;
$ret->($x * $y);
}
which at least emphasizes that the continuation is still being passed,
though it is overkill for our purposes.
Cont() method is invoked in tail position, but
we've been here before.
@EXPORT_OK rather than @EXPORT however it is
justifiable here firstly because PScm::Continuation
is part of PScheme, not a standalone library module, and secondly
the only reason another class would use PScm::Continuation
would be to gain access to the cont construct.
The reasoning is that each call to Eval() within the interpreter
corresponds to a value being calculated and, most importantly,
returned in the
PScheme language. These points of return are exactly the points that
require continuations to be used instead.
If however in the later CPS rewrite of the object system
from Chapter 12 we wanted to allow PScheme objects
to supply some sort of to-string method, and have that called
in preference to the underlying Perl as_string() method,
then we would have to rewrite as_string() into CPS.
factorial() example before TCO, where the stack built up
during calls to factorial() and built up further when the
continuations actually triggered on factorial(0). Well the
return in the PScm::Continuation::Cont() method
takes care of the second of these contingencies, and returning a
continuation here takes care of the first.
If you don't believe me, wait until we have rewritten the complete
interpreter in CPS then enter the following definition in
t/interactive:
> (define factorial > (lambda (x) > (if x > (* x (factorial (- x 1))) > 1)))Then try
> (factorial 170) 7257415615307998967396728211129263114716991681296451376543577798900561 8434017061578523507492426174595114909912378385207766660225654427530253 2890077320751090240043028005829560396661259965825710439855829425756896 6313439612262571094946806711205568880457193340212661452800000000000000 000000000000000000000000000Perl would have complained long before it hit that many levels of recursion.
undef is not the same
as returning undef, the trampoline will never see
this undef and terminate the computation prematurely.