Chapter 6. Recursion and letrec

Let's try a little experiment with the interpreter version 0.0.2. We'll try to use let to define a recursive function, the perennial factorial function14.

> (let ((factorial
>       (lambda (n)
>               (if n
>                   (* n (factorial (- n 1)))
>                   1))))
>      (factorial 3))
Error: no binding for factorial in PScm::Env

[download]

It didn't work. The reason that it didn't work is obvious, considering how let works.

let evaluates the expression half of its bindings in the enclosing environment, before it binds the values to the symbols in a new environment, so it is the enclosing environment (the global environment in this case) that the lambda captures. Now that environment doesn't have a binding for factorial, factorial is only visible within the body of the let, so any recursive call to factorial from the body of the function (closure) is bound to fail.

Putting it another way, let will create a binding for factorial, but only by extending the global environment after the lambda expression has been evaluated, in the global environment, therefore capturing the global environment.

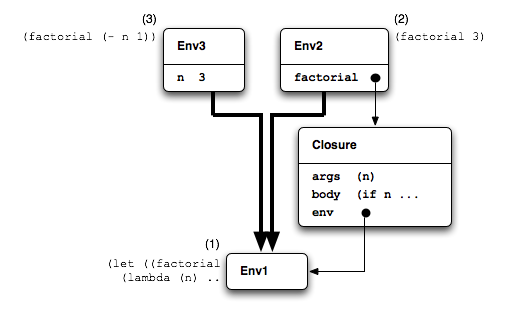
So the error is not coming from the call to (factorial 3), it's coming from the attempted recursive call to (factorial (- n 1)) inside the body of the factorial definition. The environment diagram in Figure 16 should help to make that clear.

Figure 16. Why recursion doesn't work
figure

The let evaluates the lambda expression in the initial environment, Env1 at (1), so that's the environment that gets captured by the Closure. Then the let binds the closure to the symbol factorial in an extended environment Env2, and that's where the body of the let, (factorial 3), gets evaluated at (2). Now after evaluating its argument 3 in Env2, the closure proceeds to extend the environment it captured, the global environment Env1, with a binding of n to 3 producing Env3. It's in Env3 that the body of the factorial function gets evaluated at (3). Now n has a binding in that environment, but unfortunately factorial doesn't, so the recursive call fails.

6.1. letrec

What we need is a variation of let that arranges to evaluate the values for its bindings in an environment where the bindings are already in place. Essentially the environments would appear as in Figure 17.

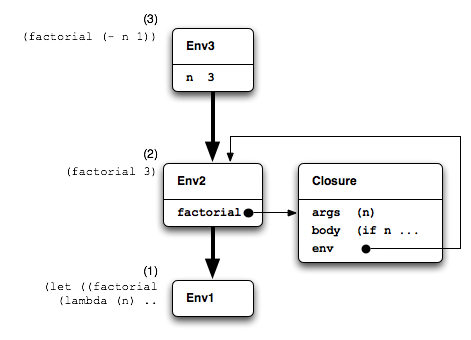
Figure 17. Recursive environments
figure

In this figure the closure has been persuaded to capture an environment Env2 containing a binding that refers back to the closure itself (a circular reference in effect.) In this circumstance any recursive call to factorial from the body of the closure would work because the closure would have extended Env2 and its body would execute in a context (Env3) where factorial did have a value.

The special form we're looking for is called letrec (short for “let recursive”) and it isn't too tricky, although a bit of a hack. Let's first remind ourselves how let works.

  1. Evaluate the value component of each binding in the current, passed in environment;
  2. Create a new environment as an extension of the current one, with those values bound to their symbols;
  3. Evaluate the body of the let in that new environment.

Our variant, letrec, isn't all that different. What it does is:

  1. Create a new extended environment first, with dummy values bound to the symbols;
  2. Evaluate the values in that new environment;
  3. Assign the values to their symbols in that new environment;
  4. Evaluate the body in that new environment.

Obviously if any of the values in a letrec are expressions other than lambda expressions, and they make reference to other letrec values in the same scope, then there will be problems. Remember that all lambda does is to capture the current environment along with formal arguments and function body. It does not immediately evaluate anything in that captured environment. For that reason real letrec implementations may typically only allow lambda expressions as values. PScheme doesn't bother making that check15.

6.1.1. Assignment

To implement letrec then, we first need to add a method to the environment class PScm::­Env that will allow assignment to existing bindings. Here is that method.

 59 sub Assign {
 60     my ($self, $symbol, $value) = @_;
 61 
 62     if (defined(my $ref = $self->_lookup_ref($symbol))) {
 63         $$ref = $value;
 64     } else {
 65         die "no binding for @{[$symbol->value]}",
 66           " in @{[ref($self)]}\n";
 67     }
 68 }

Assign() uses a helper function _lookup­_ref() to actually do the symbol lookup. If _lookup­_ref() finds a binding, then Assign() puts the new value in place through the reference that _lookup­_ref() returns. It is an error if there's not currently such a symbol in the environment. This makes sense because it keeps the distinction between variable binding and assignment clear: variable binding creates a new binding; assignment changes an existing one.

_lookup­_ref() is simple enough, it does pretty much what LookUp() does, except it returns a reference to what it finds, and returns undef, rather than die()-ing if it doesn't find a value:

 70 sub _lookup_ref {
 71     my ($self, $symbol) = @_;
 72 
 73     if (exists($self->{bindings}{ $symbol->value })) {
 74         return \$self->{bindings}{ $symbol->value };
 75     } elsif ($self->{parent}) {
 76         return $self->{parent}->_lookup_ref($symbol);
 77     } else {
 78         return undef;
 79     }
 80 }

Incidentally, LookUp() itself has been modified and simplified to make use of it.

 48 sub LookUp {
 49     my ($self, $symbol) = @_;
 50 
 51     if (defined(my $ref = $self->_lookup_ref($symbol))) {
 52         return $$ref;
 53     } else {
 54         die "no binding for @{[$symbol->value]}",
 55           " in @{[ref($self)]}\n";
 56     }
 57 }

6.1.2. PSCM::LetRec itself

All that remains to be done is to add a LetRec subclass of PScm::­SpecialForm with an Apply() method that implements the algorithm we've discussed, then add a binding in the initial environment from “letrec” to an instance of that class.

We can simplify things a bit by subclassing PScm::­SpecialForm::­Let instead of PScm::­SpecialForm, and factoring common code out of PScm::­SpecialForm::­Let's Apply() method into a new UnPack() method in that class. So first here's the new version of PScm::SpecialForm::Let::Apply() 

 12 sub Apply {
 13     my ($self, $form, $env) = @_;
 14 
 15     my ($ra_symbols, $ra_values, $body) = $self->UnPack($form, $env);
 16 
 17     return $body->Eval($env->Extend($ra_symbols, $ra_values));
 18 }

The common code in PScm::SpecialForm::Let::UnPack() just unpacks the symbols, bindings and body from the argument $form and returns them:

 20 sub UnPack {
 21     my ($self, $form, $env) = @_;
 22 
 23     my ($bindings, $body) = $form->value;
 24     my (@symbols, @values);
 25 
 26     foreach my $binding ($bindings->value) {
 27         my ($symbol, $value) = $binding->value;
 28         push @symbols, $symbol;
 29         push @values,  $value;
 30     }
 31 
 32     return (\@symbols, \@values, $body);
 33 }

Now, our new Apply() in PScm::­SpecialForm::­LetRec makes use of that same UnPack() method (by inheriting from PScm::­SpecialForm::­Let). It differs from the original Apply() only in that it calls the environment's ExtendRecursively() method, rather than Extend().

 36 package PScm::SpecialForm::LetRec;
 37 
 38 use base qw(PScm::SpecialForm::Let);
 39 
 40 sub Apply {
 41     my ($self, $form, $env) = @_;
 42 
 43     my ($ra_symbols, $ra_values, $body) = $self->UnPack($form, $env);
 44 
 45     return $body->Eval(
 46         $env->ExtendRecursively($ra_symbols, $ra_values));
 47 }

So we need to take a look at that ExtendRecursively() method in PScm::­Env.

 31 sub ExtendRecursively {
 32     my ($self, $ra_symbols, $ra_values) = @_;
 33 
 34     my $newenv = $self->ExtendUnevaluated($ra_symbols, $ra_values);
 35     $newenv->_eval_values();
 36     return $newenv;
 37 }

It creates a new environment by extending the current environment, $self with the symbols bound to their unevaluated values. Then it calls a new, private method _eval­_values() on the new environment. Here's that method:

 39 sub _eval_values {
 40     my ($self) = @_;
 41     map {
 42         $self->{bindings}{$_} =
 43           $self->{bindings}{$_}->Eval($self)
 44       }
 45       keys %{ $self->{bindings} };
 46 }

All that does is to loop over all of its bindings, replacing the unevaluated expression with the result of evaluating the expression in the current environment. Since all of those expressions are expected to be lambda expressions, the resulting closures capture the environment that they are themselves bound in. QED.

A careful reader may have realised that a valid alternative implementation of letrec would just create an empty environment extension, then populate the environment afterwards with an alternative version of Assign() which did not require the symbols to pre-exist in the environment. The main reason it is not done that way is that the current behaviour of Assign() is more appropriate for later extensions to the interpreter.

Just to be complete, here's the new version of PScm::ReadEvalPrint() with the binding for letrec.

 31 sub ReadEvalPrint {
 32     my ($infh, $outfh) = @_;
 33 
 34     $outfh ||= new FileHandle(">-");
 35     my $reader = new PScm::Read($infh);
 36     while (defined(my $expr = $reader->Read)) {
 37         my $result = $expr->Eval(
 38             new PScm::Env(
 39                 let    => new PScm::SpecialForm::Let(),
 40                 '*'    => new PScm::Primitive::Multiply(),
 41                 '-'    => new PScm::Primitive::Subtract(),
 42                 if     => new PScm::SpecialForm::If(),
 43                 lambda => new PScm::SpecialForm::Lambda(),
 44                 letrec => new PScm::SpecialForm::LetRec(),
 45             )
 46         );
 47         $result->Print($outfh);
 48     }
 49 }

6.2. Summary

Let evaluates the values of its bindings in the enclosing environment. Then it creates an extended environment in which to evaluate the body of the let expression. This means that recursive lambda expressions defined by let won't work, because there's no binding for the recursive function when the lambda expression is evaluated. In order to get recursion to work, we needed to create a variant of let, called letrec (let recursive) which sets up a dummy environment with stub values for the symbols in which to evaluate the lambda expressions, so that the lambda expressions could capture that environment in their resulting closures. Having evaluated those expressions, letrec assigns their values to the existing bindings in the new environment, replacing the dummy values. Thus when the closure executes later, the environment it has captured, and which it will extend with its formal arguments bound to actual values, will contain a reference to the closure itself, so a recursive call is successful.

6.3. Tests

The tests for the letrec form are in t/PScm_Letrec.t which you can see in Listing 14.

Listing 14. t/PScm_Letrec.t
  1 use strict;
  2 use warnings;
  3 use Test::More;
  4 use lib './t/lib';
  5 use PScm::Test tests => 4;
  6 
  7 BEGIN { use_ok('PScm') }
  8 
  9 ok(
 10     !defined(eval {
 11             evaluate(<<EOF) }), 'let does not support recursion');
 12 (let ((factorial
 13         (lambda (n)
 14           (if n (* n (factorial (- n 1)))
 15                 1))))
 16   (factorial 4))
 17 EOF
 18 
 19 is($@, "no binding for factorial in PScm::Env\n",
 20     'let does not support recursion [2]');
 21 
 22 eval_ok(<<EOF, "24", 'letrec and recursion');
 23 (letrec ((factorial
 24            (lambda (n)
 25              (if n (* n (factorial (- n 1)))
 26                    1))))
 27   (factorial 4))
 28 EOF
 29 
 30 # vim: ft=perl

There are three tests. The first two, just prove what we already know, that let does not (and should not) support recursion. The other new test replaces let with letrec and proves that letrec on the other hand does support recursive function definitions.

Full source code for this version of the interpreter is available at
http://billhails.net/Book/releases/PScm-0.0.3.tgz
Last updated Tue Mar 18 21:59:29 2008 UST

Valid CSS!

14 Factorial(n), often written n!, is n × (n - 1) × (n - 2) × ... × 1.
15 One possible way to detect this type of error would be to bind dummy objects to the symbols. These dummy objects would have an Eval() method that would die() with an informative error message if it was ever called.