let does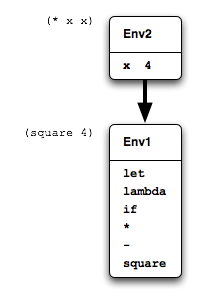
lambdaHaving derived an environment passing interpreter in version 0.0.1, the addition of functions, specifically closures, becomes much more tractable.
So far the text has been pretty relaxed about the uses of the words function and closure, which is ok because in PScheme and Perl all functions are in fact closures. But before we go any further we'd better have a clearer definition of what a closure is, and what the difference between a function and a closure might be.
First of all what precisely is a function? On consideration,
functions are a lot like let expressions: they both extend an
environment then execute an expression in the extension. A let
expression extends an environment with key-value pairs, then evaluates
its body in that new environment. A function extends an environment
by binding its formal arguments to its actual arguments12
then evaluates its body in that new environment. For example,
assuming the definition:
(define square (lambda (x) (* x x)))
then while executing the expression:
(square 4)
the global environment would be extended with a binding of x
to 4, and the body of the function, (* x x) would be
evaluated in that new environment, as in Figure 10.
let does
Now, a closure is simply a function that when executed will extend the environment that was current at the time the closure was created. Consider an example we've seen before.
> (define times2 > (let ((n 2)) > (lambda (x) (* n x)))) times2 > (times2 4) 8
The lambda expression is being executed in an environment where
n is bound to 2. The result of that lambda
expression, a closure, is also the result of the let expression
and therefore gets bound to the symbol times2 in the
global environment.
Now when times2 is called, the closure body (* n x)
must execute in an environment where
n is still bound to 2, as in Figure 11.
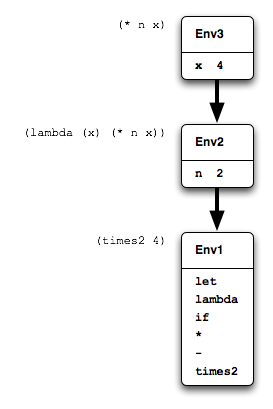
So referring to that figure: let extended the global environment
to Env2 with a binding of n to 2.
Then the closure, when it was created by lambda in
Env2, must have somehow held on to, or “captured”
Env2, so that when the closure is later executed
Env2 is the one that it extends to Env3
with its own argument x.
A function which is not a closure would have to pick a different environment to extend. It could choose the environment it is being executed in but that would cause horrendous confusion: any variables referred to in the function body that were not declared by the function might pick up values randomly from the callers environment. Alternatively it could extend the global environment. The latter choice is the standard one for non-closure implementations, but as already noted all functions in PScheme are closures (and there are no advantages to them not being closures) so we don't have to worry about that.
So we're going to continue to use the words function and closure pretty much interchangeably, but when we use the word function we're emphasizing the functional aspects of the object under discussion, and when we use the word closure, we're emphasizing its environmental behaviour.
When considering the actual implementation of closures (functions) there
are two parts to the story. The
first part is how lambda creates a closure, and the second is how
the closure gets evaluated when it is called. In the next section we'll
look at the first part, how lambda creates a closure.
lambdaWe need a good, simple example of closures in action. The following example fits our purposes, but is a bit more complicated than the examples we've seen so far:
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
This example is
not much different from our earlier times2 example,
except that an outer let provides bindings for both times2
and a variable a that will be argument to times2.
It is however just a little tricky, so in detail:
let reads: “let a be 4
and times2 be the result of
evaluating the inner let in the expression (times2 a).”let reads “let n be 2 in the
expression (lambda ...).”let is the result of evaluating that
lambda expression and thus a closure, and that is what gets bound
to the symbol times2 by the outer let.(times2 a) is evaluated, the closure bound to
times2 can still “see” the variable n
from the environment that was current when it was created, and so
the body of the closure, (* x n), wilth x
bound to 4 and n bound to 2,
produces the expected result 8.Just to be absolutely sure that semantics of that expression are well understood, here is an equivalent in Perl:
{
my $a = 4;
my $times2 = do {
my $n = 2;
sub {
my ($x) = @_;
$x * $n;
}
};
$times2->($a);
}
Now we're going to walk through the execution of the PScheme statement in a lot more detail, considering what the interpreter is actually doing to produce the final result.
The very first thing that happens when evaluating our PScheme example
is that the outer let evaluates the number 4 in the
global environment. It does not yet bind that value to a,
it first must evaluate the expression that will be bound to
times2.
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
The next thing that happens is the outer let initiates
the evaluation of the inner let.
The inner let extends the global environment
with a binding of n to 2, as hilighted in the
following code and shown in Figure 12.
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
let binds n to
2
Then, in that new environment, labelled Env2,
the let evaluates the lambda expression:
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
Evaluating a lambda expression is just the same as evaluating
any other list expression, its (unevaluated) arguments are passed to
its Apply() method, along with the current environment. In our
example the arguments to the lambda's Apply() would be:
(x)(* x n)let just created, with a binding of n
to 2.To start to make this happen we first need to add a new subclass of
PScm::SpecialForm, rather unsurprisingly called
PScm::SpecialForm::Lambda, and we need to add a binding
from the symbol lambda to an object of that class in the initial
environment. Firstly, here's ReadEvalPrint() with the additional
binding:
31 sub ReadEvalPrint { 32 my ($infh, $outfh) = @_; 33 34 $outfh ||= new FileHandle(">-"); 35 my $reader = new PScm::Read($infh); 36 while (defined(my $expr = $reader->Read)) { 37 my $result = $expr->Eval( 38 new PScm::Env( 39 let => new PScm::SpecialForm::Let(), 40 '*' => new PScm::Primitive::Multiply(), 41 '-' => new PScm::Primitive::Subtract(), 42 if => new PScm::SpecialForm::If(), 43 lambda => new PScm::SpecialForm::Lambda(), 44 ) 45 ); 46 $result->Print($outfh); 47 } 48 }
The only change is the addition of line 43
with the new binding for lambda.
Now we can look at that new package
PScm::SpecialForm::Lambda. All its Apply() method has
to do is to store the details of the function definition and the current
environment in another new type of object representing the closure:
45 package PScm::SpecialForm::Lambda; 46 47 use base qw(PScm::SpecialForm); 48 use PScm::Closure; 49 50 sub Apply { 51 my ($self, $form, $env) = @_; 52 53 my ($args, $body) = $form->value; 54 return PScm::Closure::Function->new($args, $body, $env); 55 } 56 57 1;
On
line 53
it unpacks
the formal arguments (i.e. (x)) and body
((* x n)) of its argument $form (the arguments to
the lambda expression) and on line 54 it returns a new PScm::Closure::Function
object containing those values and, most importantly, also containing
the current environment (Env2 in our example.)
That PScm::Closure::Function::new() method
(actually in PScm::Closure)
does no more than bundle its arguments:
7 sub new { 8 my ($class, $args, $body, $env) = @_; 9 10 bless { 11 args => $args, 12 body => $body, 13 env => $env, 14 }, $class; 15 }
So in our example it is Env2 that is captured, along with the arguments and body of the function, in the resulting closure. This is shown in Figure 13.
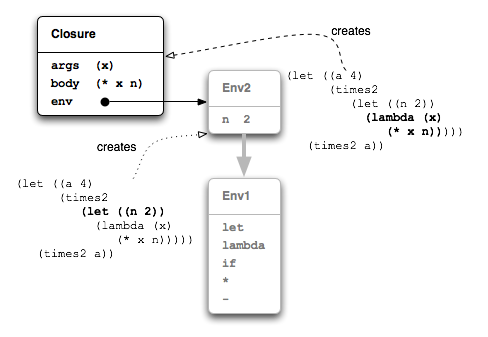
As we've noted, the value of the inner let expression
is that new Closure object, and next the outer
let recieves the value of the inner let, and
extends the global environment with a binding of times2 to
that.
It also binds a to 4:
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
The resulting environment is labelled Env3 in Figure 14.
let binds times2 and a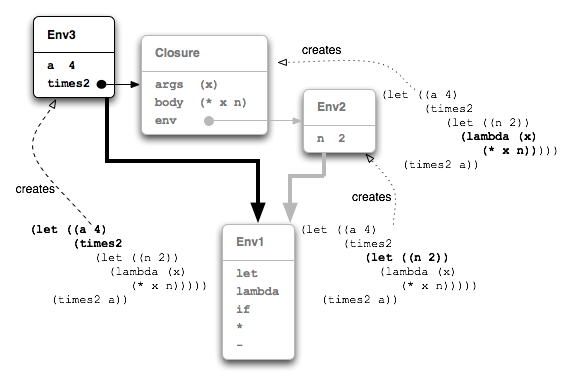
Now at this point the only thing hanging on to the old
Env2, where n has a value, is that
Closure, and the only thing hanging on to the
Closure is the binding for times2
in Env3 (the code for the Apply() method of the outer let
is currently holding on to Env3.)
Having created Env3, the outer let
evaluates its body, (times2 a) in that environment.
> (let ((a 4) > (times2 > (let ((n 2)) > (lambda (x) > (* x n))))) > (times2 a)) 8
That brings us to the second part of our story, how a function (a closure) gets evaluated.
To recap, we've reached the stage where the subexpression
(times2 a) is about to be evaluated. It will
be evaluated in the context of Env3 from
Figure 14
which
the outer let has just set up with a binding of a
to 4 and times2 to the closure.
Since (times2 a) is a list,
the Eval() method for lists comes in to play again.
It evaluates the first component of the list, the symbol
times2, in the context of Env3 resulting in the
Closure. Then it passes the rest of the form
(a list containing the symbol a) unevaluated,
along with the current environment Env3, to
the closure's Apply() method. Closures, being operations,
have to have an Apply() method, and here it is:
43 sub Apply { 44 my ($self, $form, $env) = @_; 45 46 my @evaluated_args = map { $_->Eval($env) } $form->value; 47 return $self->_apply(@evaluated_args); 48 }
First of all, on line 46 it evaluates each component of the form
(each argument to the function) with map, passing the
argument $env (Env3) to each call
to Eval(). After all, closures are functions, and functions take
their arguments evaluated.
At line 47
our closure's Apply()
returns
the result of calling a separate _apply() method on
those evaluated arguments, much as primitive operations do. Note
particularily that it does not pass its argument $env to the
private _apply() method.
The private _apply() method
is in the parent PScm::Closure class13:
21 sub _apply { 22 my ($self, @args) = @_; 23 24 my $extended_env = 25 $self->env->ExtendUnevaluated([$self->args], [@args]); 26 return $self->body->Eval($extended_env); 27 }
This _apply() method does not need an argument environment
because the correct environment to extend is the one that was
captured as part of the closure object. On line 24 It extends that previously
captured environment with bindings from its formal arguments, also
collected when the closure was created (i.e. x), to the
actual arguments it was passed (i.e. 4, already evaluated).
Because the arguments are already evaluated, it must call a new variant
of PScm::Env::Extend() called ExtendUnevaluated(),
which does just that.
Lastly _apply()() evaluates its body (the body of the function, (* x
n)) passing that extended environment as argument and returns
the result (line 26).
Returning to our example, we're still considering the evaluation
of the subexpression (times2 a). As we've said
the closure's Apply() method evaluates its argument
a in the environment it was passed, Env3,
resulting in 4.
But it is the captured environment, Env2, that
the closure extends with a binding of x to
4, resulting in Env4
(Figure 15).
It is in Env4, with x bound to 4 and
n still bound to 2, that the closure executes the body
of the function (* x n).
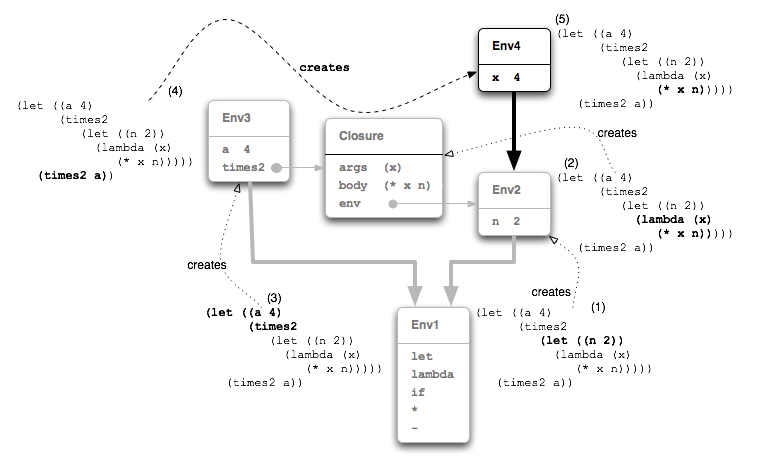
Figure 15 pretty much tells the whole story. Here's our example one last time so it can be walked through referring to the figure:
(let ((a 4)
(times2
(let ((n 2))
(lambda (x)
(* x n)))))
(times2 a))
let extends the global env
Env1 with a binding of n to 2
producing Env2.let then evaluates the lambda expression in
the context of Env2, creating a Closure
that captures Env2.let extends the global environment
Env1 with bindings of a to 4
and times2 to the value of the inner let: the
Closure.let evaluates the subexpression (times2 a)
in the context of Env3. In this environment times2
evaluates to the closure, and its Apply() evaluates a in the
same environment Env3 where it evaluates to 4.x to 4
producing Env4 and evaluates its body, (* x n),
in this environment.It would be nice if, when given a closure to print, PScheme
could produce something a bit more informative that the unhelpful
“PScm::Closure::Function” that results from the default
as_string() method in the top-level PScm package.
We could instead print a representation of the lambda expression
that created the closure. For example.
> (let ((square > (lambda (x) > (* x x)))) > square) (lambda (x) (* x x))
This is trivially accomplished by overriding
the default as_string() method in PScm::Closure.
Here's that override.
29 sub as_string { 30 my ($self) = @_; 31 return PScm::Expr::List->new( 32 $self->_symbol, 33 $self->{args}, 34 $self->{body} 35 )->as_string; 36 }
All it does is to construct a new PScm::Expr::List
containing the symbol that constructed the closure (lambda)
the formal arguments to the closure and the body of the closure.
It then calls that list's as_string() method and returns
the result. The aquisition of the lambda symbol is deferred to
a separate method _symbol() in PScm::Closure::Function
(again because later later versions of the interpreter will have
different kinds of closures). Here's _symbol().
50 sub _symbol { 51 PScm::Expr::Symbol->new('lambda'); 52 }
Job done. Closures, when printed, will now produce a useful representation of the function they perform.
Hopefully the power, flexibility and elegance of an environment-passing interpreter combined with a linked-list environment implementation is becoming apparent. The enormous advantage over a stack discipline is that individual environments need not go away just because a particular construct returns. They can hang around as long as they are needed and garbage collection will remove them when the time comes. Without further ado then, here's the full source for our new PScm::Closure package in Listing 12.
PScm/Closure.pm1 package PScm::Closure; 2 3 use strict; 4 use warnings; 5 use base qw(PScm); 6 7 sub new { 8 my ($class, $args, $body, $env) = @_; 9 10 bless { 11 args => $args, 12 body => $body, 13 env => $env, 14 }, $class; 15 } 16 17 sub args { $_[0]->{args}->value } 18 sub body { $_[0]->{body} } 19 sub env { $_[0]->{env} } 20 21 sub _apply { 22 my ($self, @args) = @_; 23 24 my $extended_env = 25 $self->env->ExtendUnevaluated([$self->args], [@args]); 26 return $self->body->Eval($extended_env); 27 } 28 29 sub as_string { 30 my ($self) = @_; 31 return PScm::Expr::List->new( 32 $self->_symbol, 33 $self->{args}, 34 $self->{body} 35 )->as_string; 36 } 37 38 ################################ 39 package PScm::Closure::Function; 40 41 use base qw(PScm::Closure); 42 43 sub Apply { 44 my ($self, $form, $env) = @_; 45 46 my @evaluated_args = map { $_->Eval($env) } $form->value; 47 return $self->_apply(@evaluated_args); 48 } 49 50 sub _symbol { 51 PScm::Expr::Symbol->new('lambda'); 52 } 53 54 1;
You can see the tests for the lambda form in a new file,
t/PScm_Lambda.t, in
Listing 13.
t/PScm_Lambda.t1 use strict; 2 use warnings; 3 use Test::More; 4 use lib './t/lib'; 5 use PScm::Test tests => 5; 6 use FileHandle; 7 8 BEGIN { use_ok('PScm') } 9 10 eval_ok(<<EOF, '16', 'lambda'); 11 (let ((square 12 (lambda (x) (* x x)))) 13 (square 4)) 14 EOF 15 16 eval_ok(<<EOF, '(lambda (x) (* x x))', 'lambda to string'); 17 (let ((square 18 (lambda (x) (* x x)))) 19 square) 20 EOF 21 22 eval_ok(<<EOF, '12', 'closure'); 23 (let ((times3 24 (let ((n 3)) 25 (lambda (x) (* n x))))) 26 (times3 4)) 27 EOF 28 29 eval_ok(<<EOF, '15', 'higher order functions'); 30 (let ((times3 31 (let ((makemultiplier 32 (lambda (n) 33 (lambda (x) (* n x))))) 34 (makemultiplier 3)))) 35 (times3 5)) 36 EOF 37 38 # vim: ft=perl
The first test exercizes the simple
creation of a lambda expression, its binding to a symbol,
and its application to arguments. The second
works through pretty much exactly the example we've been
working through. The third starts to
flex the muscles of our nascent interpreter a little more. It creates
a local makemultiplier function that when called with an argument
n will return another function that will multiply n by its argument.
It then binds the result of calling (makemultiplier 3) to times3
and calls (times3 5), confirming that the result is 15, as expected.
Incidentally, this demonstrates that the environment created by a
lambda expression is equally ameanable to capture by a closure.
We could rewrite the body of that last test in Perl as follows:
{
my $times3 = do {
my $makemultiplier = sub {
my ($n) = @_;
return sub {
my ($x) = @_;
return $n * $x;
}
};
$makemultiplier->(3);
};
$times3->(5);
}
Full source code for this version of the interpreter is available athttp://billhails.net/Book/releases/PScm-0.0.2.tgz