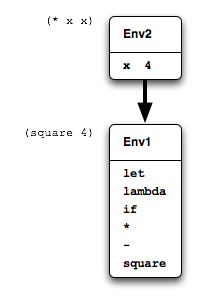
Implementing lambda

Having derived an environment passing interpreter in version 0.0.1, the addition of functions, specifically closures, becomes much more tractable.

So far the text has been pretty relaxed about the uses of the words function and closure, which is ok because in PScheme and Perl all functions are in fact closures. But before we go any further we'd better have a clearer definition of what a closure is, and what the difference between a function and a closure might be.

First of all what precisely is a function? On consideration, functions are a lot like let expressions: they both extend an environment then execute an expression in the extension. A let expression extends an environment with key-value pairs, then evaluates its body in that new environment. A function extends an environment by binding its formal arguments to its actual arguments¹⁴ then evaluates its body in that new environment. For example, assuming the definition:

the global environment would be extended with a binding of x to 4, and the body of the function, (* x x) would be evaluated in that new environment, as in Figure 5.1.

Now, a closure is simply a function that when executed will extend the environment that was current at the time the closure was created. Consider an example we've seen before.

The lambda expression is being executed in an environment where n is bound to 2. The result of that lambda expression, a closure, is also the result of the let expression and therefore gets bound to the symbol times2 in the global environment.

Now when times2 is called, the closure body (* n x) must execute in an environment where n is still bound to 2, as in Figure 5.2.

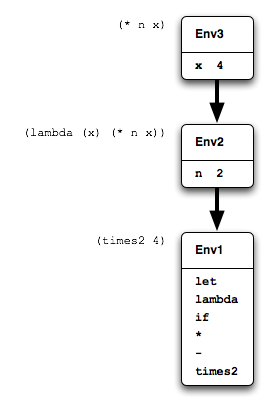
So referring to that figure: let extended the global environment to Env2 with a binding of n to 2. Then the closure, when it was created by lambda in Env2, must have somehow held on to, or “captured” Env2, so that when the closure is later executed Env2 is the one that it extends to Env3 with its own argument x.

A function which is not a closure would have to pick a different environment to extend. It could choose the environment it is being executed in but that would cause horrendous confusion: any variables referred to in the function body that were not declared by the function might pick up values randomly from the callers environment. Alternatively it could extend the global environment. The latter choice is the standard one for non-closure implementations, but as already noted all functions in PScheme are closures (and there are no advantages to them not being closures) so we don't have to worry about that.

So we're going to continue to use the words function and closure pretty much interchangeably, but when we use the word function we're emphasizing the functional aspects of the object under discussion, and when we use the word closure, we're emphasizing its environmental behaviour.

When considering the actual implementation of closures (functions) there are two parts to the story. The first part is how lambda creates a closure, and the second is how the closure gets evaluated when it is called. In the next section we'll look at the first part, how lambda creates a closure.

5.1. `lambda`

We need a good, simple example of closures in action. The following example fits our purposes, but is a bit more complicated than the examples we've seen so far:

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

This example is not much different from our earlier times2 example, except that an outer let provides bindings for both times2 and a variable a that will be argument to times2. It is however just a little tricky, so in detail:

The outer let reads: “let a be 4 and times2 be the result of evaluating the inner let in the expression (times2 a).”
The inner let reads “let n be 2 in the expression (lambda ...).”
The value of that inner let is the result of evaluating that lambda expression and thus a closure, and that is what gets bound to the symbol times2 by the outer let.
When (times2 a) is evaluated, the closure bound to times2 can still “see” the variable n from the environment that was current when it was created, and so the body of the closure, (* x n), wilth x bound to 4 and n bound to 2, produces the expected result 8.

Just to be absolutely sure that semantics of that expression are well understood, here is an equivalent in Perl:

{
    my $a = 4;
    my $times2 = do {
        my $n = 2;
        sub {
            my ($x) = @_;
            $x * $n;
        }
    };
    $times2->($a);
}
[download]

Now we're going to walk through the execution of the PScheme statement in a lot more detail, considering what the interpreter is actually doing to produce the final result.

The very first thing that happens when evaluating our PScheme example is that the outer let evaluates the number 4 in the global environment. It does not yet bind that value to a, it first must evaluate the expression that will be bound to times2.

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

The next thing that happens is the outer let initiates the evaluation of the inner let. The inner let extends the global environment with a binding of n to 2, as hilighted in the following code and shown in Figure 5.3.

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

Figure 5.3. let binds n to 2

Then, in that new environment, labelled Env2, the let evaluates the lambda expression:

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

Evaluating a lambda expression is just the same as evaluating any other list expression, its (unevaluated) arguments are passed to its Apply() method, along with the current environment. In our example the arguments to the lambda's Apply() would be:

A list of the unevaluated arguments containing
1. the formal arguments to the function: (x)
2. the body of the function: (* x n)
the current environment, Env2 that the let just created, with a binding of n to 2.

To start to make this happen we first need to add a new subclass of PScm::SpecialForm, rather unsurprisingly called PScm::SpecialForm::Lambda, and we need to add a binding from the symbol lambda to an object of that class in the initial environment. Firstly, here's ReadEvalPrint() with the additional binding:

 31 sub ReadEvalPrint {
 32     my ($infh, $outfh) = @_;
 33 
 34     $outfh ||= new FileHandle(">-");
 35     my $reader = new PScm::Read($infh);
 36     while (defined(my $expr = $reader->Read)) {
 37         my $result = $expr->Eval(
 38             new PScm::Env(
 39                 let    => new PScm::SpecialForm::Let(),
 40                 '*'    => new PScm::Primitive::Multiply(),
 41                 '-'    => new PScm::Primitive::Subtract(),
 42                 if     => new PScm::SpecialForm::If(),
 43                 lambda => new PScm::SpecialForm::Lambda(),
 44             )
 45         );
 46         $result->Print($outfh);
 47     }
 48 }

The only change is the addition of Line 43 with the new binding for lambda.

Now we can look at that new package PScm::SpecialForm::Lambda. All its Apply() method has to do is to store the details of the function definition and the current environment in another new type of object representing the closure:

 45 package PScm::SpecialForm::Lambda;
 46 
 47 use base qw(PScm::SpecialForm);
 48 use PScm::Closure;
 49 
 50 sub Apply {
 51     my ($self, $form, $env) = @_;
 52 
 53     my ($args, $body) = $form->value;
 54     return PScm::Closure::Function->new($args, $body, $env);
 55 }
 56 
 57 1;

On Line 53 it unpacks the formal arguments (i.e. (x)) and body ((* x n)) of its argument $form (the arguments to the lambda expression) and on Line 54 it returns a new PScm::Closure::Function object containing those values and, most importantly, also containing the current environment (Env2 in our example.)

That PScm::Closure::Function::new() method (actually in PScm::Closure) does no more than bundle its arguments:

  7 sub new {
  8     my ($class, $args, $body, $env) = @_;
  9 
 10     bless {
 11         args => $args,
 12         body => $body,
 13         env  => $env,
 14     }, $class;
 15 }

So in our example it is Env2 that is captured, along with the arguments and body of the function, in the resulting closure. This is shown in Figure 5.4.

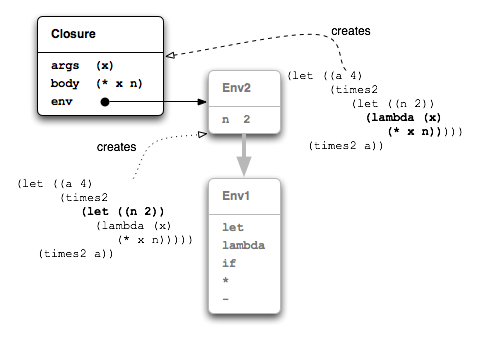
Figure 5.4. Closure Captures the Local Environment

As we've noted, the value of the inner let expression is that new Closure object, and next the outer let recieves the value of the inner let, and extends the global environment with a binding of times2 to that. It also binds a to 4:

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

The resulting environment is labelled Env3 in Figure 5.5.

Figure 5.5. let binds times2 and a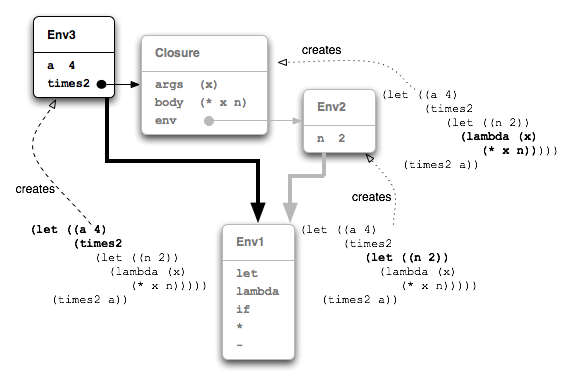

Now at this point the only thing hanging on to the old Env2, where n has a value, is that Closure, and the only thing hanging on to the Closure is the binding for times2 in Env3 (the code for the Apply() method of the outer let is currently holding on to Env3.)

Having created Env3, the outer let evaluates its body, (times2 a) in that environment.

> (let ((a 4)
>       (times2
>         (let ((n 2))
>           (lambda (x)
>              (* x n)))))
>   (times2 a))
8
[download]

That brings us to the second part of our story, how a function (a closure) gets evaluated.

5.2. Evaluating a Closure

To recap, we've reached the stage where the subexpression (times2 a) is about to be evaluated. It will be evaluated in the context of Env3 from Figure 5.5 which the outer let has just set up with a binding of a to 4 and times2 to the closure.

Since (times2 a) is a list, the Eval() method for lists comes in to play again. It evaluates the first component of the list, the symbol times2, in the context of Env3 resulting in the Closure. Then it passes the rest of the form (a list containing the symbol a) unevaluated, along with the current environment Env3, to the closure's Apply() method. Closures, being operations, have to have an Apply() method, and here it is:

 43 sub Apply {
 44     my ($self, $form, $env) = @_;
 45 
 46     my @evaluated_args = map { $_->Eval($env) } $form->value;
 47     return $self->_apply(@evaluated_args);
 48 }

First of all, on Line 46 it evaluates each component of the form (each argument to the function) with map, passing the argument $env (Env3) to each call to Eval(). After all, closures are functions, and functions take their arguments evaluated.

At Line 47 our closure's Apply() returns the result of calling a separate _apply() method on those evaluated arguments, much as primitive operations do. Note particularily that it does not pass its argument $env to the private _apply() method.

The private _apply() method is in the parent PScm::Closure class¹⁵:

 21 sub _apply {
 22     my ($self, @args) = @_;
 23 
 24     my $extended_env =
 25       $self->env->ExtendUnevaluated([$self->args], [@args]);
 26     return $self->body->Eval($extended_env);
 27 }

This _apply() method does not need an argument environment because the correct environment to extend is the one that was captured when the the closure object was created. On Line 24 It extends that previously captured environment with bindings from its formal arguments, also collected when the closure object was created (i.e. x), to the actual arguments it was passed (i.e. 4, already evaluated). Because the arguments are already evaluated, it must call a new variant of PScm::Env::Extend() called ExtendUnevaluated(), which does just that. Lastly _apply() evaluates its body (the body of the function, (* x n)) passing that extended environment as argument and returns the result (Line 26).

Returning to our example, we're still considering the evaluation of the subexpression (times2 a). As we've said the closure's Apply() method evaluates its argument a in the environment it was passed, Env3, resulting in 4. But it is the captured environment, Env2, that the closure extends with a binding of x to 4, resulting in Env4 (Figure 5.6). It is in Env4, with x bound to 4 and n still bound to 2, that the closure executes the body of the function (* x n).

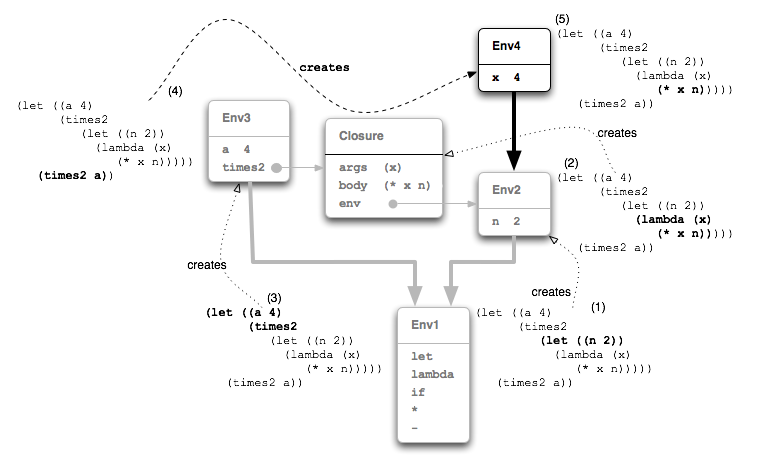
Figure 5.6. Closure Extends Captured Env

Figure 5.6 pretty much tells the whole story. Here's our example one last time so it can be walked through referring to the figure:

(let ((a 4)
      (times2
         (let ((n 2))
           (lambda (x)
              (* x n)))))
   (times2 a))
[download]

At (1) in the figure, the inner let extends the global env Env1 with a binding of n to 2 producing Env2.
At (2) the inner let then evaluates the lambda expression in the context of Env2, creating a Closure that captures Env2.
At (3), the outer let extends the global environment Env1 with bindings of a to 4 and times2 to the value of the inner let: the Closure.
At (4) the outer let evaluates the subexpression (times2 a) in the context of Env3. In this environment times2 evaluates to the closure, and its Apply() evaluates a in the same environment Env3 where it evaluates to 4.
Finally, at (5), the closure extends the originally captured environment Env2 with a binding of x to 4 producing Env4 and evaluates its body, (* x n), in this environment.

5.3. Printing a Closure

It would be nice if, when given a closure to print, PScheme could produce something a bit more informative than the unhelpful “PScm::Closure::Function” that results from the default as_string() method in the top-level PScm package. We could instead print a representation of the lambda expression that created the closure. For example.

> (let ((square
>         (lambda (x)
>           (* x x))))
>      square)
(lambda (x) (* x x))
[download]

This is trivially accomplished by overriding the default as_string() method in PScm::Closure. Here's that override.

 29 sub as_string {
 30     my ($self) = @_;
 31     return PScm::Expr::List->new(
 32         $self->_symbol,
 33         $self->{args},
 34         $self->{body}
 35     )->as_string;
 36 }

All it does is to construct a new PScm::Expr::List containing the symbol that constructed the closure (lambda) the formal arguments to the closure and the body of the closure. It then calls that list's as_string() method and returns the result. The aquisition of the lambda symbol is deferred to a separate method _symbol() in PScm::Closure::Function (again because later later versions of the interpreter will have different kinds of closures). Here's _symbol().

 50 sub _symbol {
 51     PScm::Expr::Symbol->new('lambda');
 52 }

Job done. Closures, when printed, will now produce a useful representation of the function they perform.

5.4. Summary

Hopefully the power, flexibility and elegance of an environment-passing interpreter combined with a linked-list environment implementation is becoming apparent. The enormous advantage over a stack discipline is that individual environments need not go away just because a particular construct returns. They can hang around as long as they are needed and garbage collection will remove them when the time comes. Without further ado then, here's the full source for our new PScm::Closure package in Listing 12.

Listing 12. PScm/Closure.pm

  1 package PScm::Closure;
  2 
  3 use strict;
  4 use warnings;
  5 use base qw(PScm);
  6 
  7 sub new {
  8     my ($class, $args, $body, $env) = @_;
  9 
 10     bless {
 11         args => $args,
 12         body => $body,
 13         env  => $env,
 14     }, $class;
 15 }
 16 
 17 sub args { $_[0]->{args}->value }
 18 sub body { $_[0]->{body} }
 19 sub env  { $_[0]->{env} }
 20 
 21 sub _apply {
 22     my ($self, @args) = @_;
 23 
 24     my $extended_env =
 25       $self->env->ExtendUnevaluated([$self->args], [@args]);
 26     return $self->body->Eval($extended_env);
 27 }
 28 
 29 sub as_string {
 30     my ($self) = @_;
 31     return PScm::Expr::List->new(
 32         $self->_symbol,
 33         $self->{args},
 34         $self->{body}
 35     )->as_string;
 36 }
 37 
 38 ################################
 39 package PScm::Closure::Function;
 40 
 41 use base qw(PScm::Closure);
 42 
 43 sub Apply {
 44     my ($self, $form, $env) = @_;
 45 
 46     my @evaluated_args = map { $_->Eval($env) } $form->value;
 47     return $self->_apply(@evaluated_args);
 48 }
 49 
 50 sub _symbol {
 51     PScm::Expr::Symbol->new('lambda');
 52 }
 53 
 54 1;

5.5. Tests

You can see the tests for the lambda form in a new file, t/PScm_Lambda.t, in Listing 13.

Listing 13. t/PScm_Lambda.t

  1 use strict;
  2 use warnings;
  3 use Test::More;
  4 use lib './t/lib';
  5 use PScm::Test tests => 5;
  6 use FileHandle;
  7 
  8 BEGIN { use_ok('PScm') }
  9 
 10 eval_ok(<<EOF, '16', 'lambda');
 11 (let ((square
 12        (lambda (x) (* x x))))
 13      (square 4))
 14 EOF
 15 
 16 eval_ok(<<EOF, '(lambda (x) (* x x))', 'lambda to string');
 17 (let ((square
 18        (lambda (x) (* x x))))
 19      square)
 20 EOF
 21 
 22 eval_ok(<<EOF, '12', 'closure');
 23 (let ((times3
 24       (let ((n 3))
 25            (lambda (x) (* n x)))))
 26      (times3 4))
 27 EOF
 28 
 29 eval_ok(<<EOF, '15', 'higher order functions');
 30 (let ((times3
 31       (let ((makemultiplier
 32              (lambda (n)
 33                      (lambda (x) (* n x)))))
 34            (makemultiplier 3))))
 35      (times3 5))
 36 EOF
 37 
 38 # vim: ft=perl

The first test exercizes the simple creation of a lambda expression, its binding to a symbol, and its application to arguments. The second works through pretty much exactly the example we've been working through. The third starts to flex the muscles of our nascent interpreter a little more. It creates a local makemultiplier function that when called with an argument n will return another function that will multiply n by its argument. It then binds the result of calling (makemultiplier 3) to times3 and calls (times3 5), confirming that the result is 15, as expected. Incidentally, this demonstrates that the environment created by a lambda expression is equally ameanable to capture by a closure.

We could rewrite the body of that last test in Perl as follows:

{
    my $times3 = do {
        my $makemultiplier = sub {
            my ($n) = @_;
            return sub {
                my ($x) = @_;
                return $n * $x;
            }
        };
        $makemultiplier->(3);
    };
    $times3->(5);
}
[download]

¹⁴

Formal arguments are the names that a function gives to its arguments. Actual arguments are the values passed to a function.

¹⁵

Why? Because a later version of the interpreter will support more than one type of closure.

Chapter 5. Implementing lambda

5.1. lambda

5.2. Evaluating a Closure

5.3. Printing a Closure

5.4. Summary

5.5. Tests

Chapter 5. Implementing `lambda`

5.1. `lambda`