All posts by Bill

Basics, Music, Theory

Triads

Leave a comment

The simplest chords are called triads, because they are made of three notes a third apart from one another. We can form a triad from any note by adding two notes a third and a fifth (3 plus 3 does equal 5) above it. Here’s a triad built on C.

C Major Triad

It’s a major triad because the interval from C (the root) to E (the third) is a major third. If we flattened the E then it would be a minor triad:

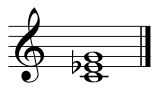
C Minor Triad

Like I said, you can form a triad on any note. Here are all the triads that you can make from the notes of C major:

C Major Triads

Notice the roman numerals. Musicians use roman numerals to identify the chords of a key. It’s useful because they are independant of the key itself, and so easier to transpose into other keys. The triad built on the first note of the key (C in this example) is given the number I, and so on. Beyond the simple use of roman numerals thare are many alternative and somewhat conflicting conventions. The one I’ve chosen is to use upper case roman numerals to indicate the major triads, and lower case to indicate the minor ones. The circle superscript of chord vii indicates it is a diminished triad, made up of two consecutive minor thirds.

This pattern of ascending chords: major, minor, minor, major, major, minor, diminished is common to all major keys.

Minor keys are different. The natural minor scale shares the same notes as the major scale a minor third above, so we have the same sequence of chords as a major key, but starting six chords in (or three chords back).

C Natural Minor Triads

The harmonic minor scale has a raised seventh. As the name suggests it is used for harmonizing melodies in minor keys:

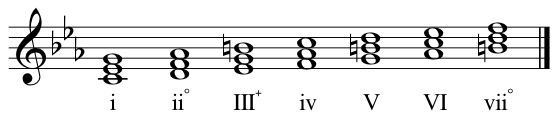
C Harmonic Minor Triads

You can see that compared to the harmonic minor, the additional raised sixth makes ii minor instead of diminished, IV major instead of minor, and vi diminished instead of major.

Apart from roman numerals, an alternative scheme which you should also be aware of is that each note of a scale and hence each chord rooted on that note and each key based on that note has a name. Here they are:

I Tonic
the “home” of the key
II Supertonic
The note/chord/key above the tonic
III Mediant
Half way between Tonic and Dominant
IV Subdominant
The same interval below the tonic as the Dominant is above (a perfect fifth)
V Dominant
The most important note/chord/key after the tonic
VI Submediant
As far below the tonic as the mediant is above
VII Leading Note
This note “leads” to the Tonic. It can be called Subtonic by analogy with Supertonic, but only if it is rooted on the minor seventh above the tonic (natural minor scale.)
Code Generation, Technology

A Slightly Non-Standard Application

Leave a comment

Here’s an application of code generation that doesn’t fit the standard Enterprise Application mold: here I’m using code generation to build a class heirarchy for abstract syntax trees.

The idea is pretty simple. An abstract syntax tree is a tree containing the results of parsing a programming language. Nodes of the tree could be function calls, operator application or control flow constructs, and the leaves of the tree would be comstants and variables. Of course these trees cannot be constructed arbitrarily, it doesn’t often make sense to add an integer to a record for example, so the constructors for the nodes need to declare (or, in an untyped language, type-check) their arguments. Each node will furthermore need accessors and probably an accept() method for the Visitor pattern, so that is a substantial amount of boiler-plate code for something that is easily describeable at a very high level.

Here’s a snapshot of the AST definition from F♮:

This is a high level but complete description of the required classes, all of the details of implementation are merely repetitive, which makes it a perfect candidate for code generation.

So, given this description, and a couple of command-line options to cover class prefixes etc., my treebuilder (tbd) will generate all of the classes required. For example, here’s the generated class definition for Expr If(Expr test, Sequence consequent, Sequence alternative):

The point of all this is to be able to use these constructors directly in a yapp or similar grammar file. Here’s a snippet of these generated classes in action:

One of the visitors over the resulting tree is a rewriting visitor that converts some abstract syntax to simpler forms so that there are fewer constructs that need to be dealt with later on. Here’s the visitor routine that converts If abstract syntax to a function call: